
【题目】如图①,已知![]() 是
是![]() 的外角
的外角![]() 的平分线,且
的平分线,且![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
(1)若![]() 恰好垂直平分
恰好垂直平分![]() ,求
,求![]() 的度数;
的度数;
(2)王涵探究后提出等式:![]() ,请通过证明判断“王涵发现”是否正确;
,请通过证明判断“王涵发现”是否正确;
(3)如图②,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的度数.
的度数.

【答案】(1)60°(2)结论错误,理由见解析(3)80°.
【解析】
(1)根据垂直平分线的性质得到![]() ,
,![]() ,再根据角平分线的性质及平角的性质即可求解;
,再根据角平分线的性质及平角的性质即可求解;
(2)根据外角定理得到![]() ,根据角平分线的性质与平行线的判定定理可知
,根据角平分线的性质与平行线的判定定理可知![]() ,故结论错误;
,故结论错误;
(3)设![]() ,
,![]() ,根据已知条件和角平分线的性质与外角定理得到关于x,y的方程组即可求解x,y,故可得到
,根据已知条件和角平分线的性质与外角定理得到关于x,y的方程组即可求解x,y,故可得到![]() 的度数.
的度数.
(1)∵![]() 垂直平分
垂直平分![]() ,
,
∴![]() ,
,![]()
则![]()
∵![]() 是
是![]() 的外角
的外角![]() 的平分线,
的平分线,
∴![]()
∴![]() =
=![]()
又![]() +
+![]() =180°
=180°
∴![]() =60°
=60°
(2)结论错误;
∵![]() 是
是![]() 的外角
的外角![]() 的平分线,
的平分线,
∴![]()
∵![]() ,
,
∴![]()
∵BE与CE相交,
∴![]()
∴![]()
故“王涵发现”错误;
(3)设![]() ,
,![]() ,
,
∵![]() 是
是![]() 的外角
的外角![]() 的平分线,
的平分线,
∴![]()
∵![]() ,
,![]()
∴![]() ,
,![]()
∵![]() ,
,
故![]()
∴![]()
∵![]()
∴![]() =2y
=2y
∴2x=3y①
∵![]()
∴![]()
故2x-y+y+x=90°②
由①②得x=30°,y=20°
∴![]() =80°.
=80°.


科目:初中数学 来源: 题型:
【题目】万圣节两周前,某商店购进1000个万圣节面具,进价为每个6元,第一周以每个10元的价格售出200个;随着万圣节的临近,预计第二周若按每个10元的价格销售可售出400个,但商店为了尽快减少库存,决定单价降价x元销售![]() 根据市场调查,单价每降低1元,可多售出100个,但售价不得低于进价
根据市场调查,单价每降低1元,可多售出100个,但售价不得低于进价![]() ;节后,商店对剩余面具清仓处理,以第一周售价的四折全部售出.
;节后,商店对剩余面具清仓处理,以第一周售价的四折全部售出.
![]() 当单价降低2元时,计算第二周的销售量和售完这批面具的总利润;
当单价降低2元时,计算第二周的销售量和售完这批面具的总利润;
![]() 如果销售完这批面具共获利1300元,问第二周每个面具的销售价格为多少元?
如果销售完这批面具共获利1300元,问第二周每个面具的销售价格为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
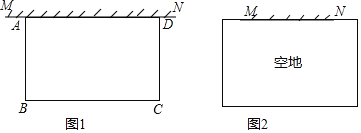
【题目】空地上有一段长为a米的旧墙MN,某人利用旧墙和木栏围成一个矩形菜园ABCD,已知木栏总长为100米.
(1)已知a=20,矩形菜园的一边靠墙,另三边一共用了100米木栏,且围成的矩形菜园面积为450平方米.如图1,求所利用旧墙AD的长;
(2)已知0<α<50,且空地足够大,如图2.请你合理利用旧墙及所给木栏设计一个方案,使得所围成的矩形菜园ABCD的面积最大,并求面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将进货单价为![]() 元的商品按
元的商品按![]() 元售出时,就能卖出
元售出时,就能卖出![]() 个.已知这种商品每个涨价
个.已知这种商品每个涨价![]() 元,其销售量就减少
元,其销售量就减少![]() 个,问为了赚得
个,问为了赚得![]() 元的利润,而成本价又不高于
元的利润,而成本价又不高于![]() 元,售价应定为多少?这时应进货多少个?
元,售价应定为多少?这时应进货多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
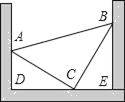
【题目】如图,把一块等腰直角三角形零件(△ABC,其中∠ACB=90°),放置在一凹槽内,三个顶点A,B,C分别落在凹槽内壁上,已知∠ADE=∠BED=90°,测得AD=5cm,BE=7cm,求该三角形零件的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是边AC上一点,连BD,给出下列条件:①∠ABD=∠ACB;②AB2=ADAC;③ADBC=ABBD;④ABBC=ACBD.其中单独能够判定△ABC∽△ADB的个数是( )
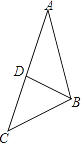
A. ①② B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程4x2+4(m﹣1)x+m2=0
(1)当m在什么范围取值时,方程有两个实数根?
(2)设方程有两个实数根x1 , x2 , 问m为何值时,x12+x22=17?
(3)若方程有两个实数根x1,x2, 问x1和x2能否同号?若能同号,请求出相应m的取值范围;若不能同号,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com