
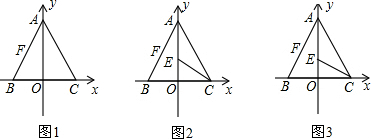
分析 (1)因为C点是B点的对称点,连接CF交OA于E,此时BE+EF的值最小,根据等边三角形的性质求得
∠BCF=30°,得出CE=2OE,然后根据勾股定理即可求得OE=1,CE=2,从而求得E点的坐标;
(2)当P点在CE上时,作PG⊥OA于G,则PG∥OC,得出$\frac{PG}{OC}$=$\frac{EP}{EC}$,求得PG=$\frac{\sqrt{3}}{2}$(2-t),根据三角形APC面积为S=S△AEP-S△AEP,即可得到S=$\frac{\sqrt{3}}{2}$t(0≤t≤2);当P点在AE上时,根据三角形面积公式得到S=$\frac{1}{2}$AP×OC=$\frac{1}{2}$(4-t)×$\sqrt{3}$=2$\sqrt{3}$-$\frac{\sqrt{3}}{2}$t(2<t≤4).
(3)分两种情况分别讨论求得即可.
解答 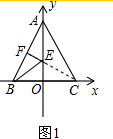 解:(1)如图1,连接CF,交OA于E,此时BE+EF的值最小,
解:(1)如图1,连接CF,交OA于E,此时BE+EF的值最小,
∵点F是AB中点,
∴∠BCF=30°,
∴CE=2OE,
设OE=x,则EC=2x,
∵EC2=OE2+OC2,OC=$\sqrt{3}$,
∴(2x)2=x2+($\sqrt{3}$)2,解得x=1,
∴OE=1,CE=2,
∴E(0,1);
故答案为(0,1);
(2)如图2,当P点在CE上时,作PG⊥OA于G,
∴PG∥OC,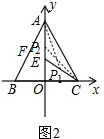
∴$\frac{PG}{OC}$=$\frac{EP}{EC}$,
∵OC=$\sqrt{3}$,CE=2,CP=t,
∴$\frac{PG}{\sqrt{3}}$=$\frac{2-t}{2}$,
∴PG=$\frac{\sqrt{3}}{2}$(2-t),
∵三角形APC面积为S=S△AEP-S△AEP,AE=3-1=2,
∴S=$\frac{1}{2}$AE•OC-$\frac{1}{2}$AE•PG=$\frac{1}{2}$×2×$\sqrt{3}$-$\frac{1}{2}$×2×$\frac{\sqrt{3}}{2}$(2-t)=$\frac{\sqrt{3}}{2}$t,
即S=$\frac{\sqrt{3}}{2}$t(0≤t≤2);
当P点在AE上时,S=$\frac{1}{2}$AP×OC=$\frac{1}{2}$(4-t)×$\sqrt{3}$=2$\sqrt{3}$-$\frac{\sqrt{3}}{2}$t,
即S=-$\frac{\sqrt{3}}{2}$t+2$\sqrt{3}$(2<t≤4).
故S与t的关系式为:S=$\left\{\begin{array}{l}{\frac{\sqrt{3}}{2}t(0≤t≤2)}\\{-\frac{\sqrt{3}}{2}t+2\sqrt{3}(2<t≤4)}\end{array}\right.$.
(3)如图3,①以A为圆心,以AF长为半径画弧,交OA于点P,则AP=AF,
∵A(0,3),B(-$\sqrt{3}$,0),
∴OA=3,OB=$\sqrt{3}$,
∴AB=2$\sqrt{3}$,
∴AF=$\sqrt{3}$,
∴AP=$\sqrt{3}$,
∴t=4-$\sqrt{3}$;
②以F为圆心,以AF长为半径画弧,交CE于点P2,则PF=AF,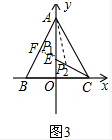
∵C($\sqrt{3}$,0),E(0,1),
∴直线CE的解析式为y=-$\frac{\sqrt{3}}{3}$x+1,
设P(x,-$\frac{\sqrt{3}}{3}$x+1),
∵A(0,3),B(-$\sqrt{3}$,0),
∴F(-$\frac{\sqrt{3}}{2}$,$\frac{3}{2}$),
∴PF2=(x+$\frac{\sqrt{3}}{2}$)2+(-$\frac{\sqrt{3}}{3}$x+1-$\frac{3}{2}$)2=AF2=($\sqrt{3}$)2,
即2x2+2$\sqrt{3}$x-3=0,
解得x=$\frac{-\sqrt{3}+3}{2}$,
∴P($\frac{3-\sqrt{3}}{2}$,$\frac{3-\sqrt{3}}{2}$).
∴t=3-$\sqrt{3}$,
∴在(2)的条件下,t=4-$\sqrt{3}$或3-$\sqrt{3}$时,三角形AFP是等腰三角形.
点评 本题是一次函数的综合题,考查了等边三角形的性质,直角三角形的性质,勾股定理的应用,待定系数法求一次函数的解析式,三角形的面积等,分类讨论思想的运用是解题的关键.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:选择题
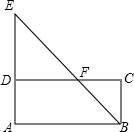 如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )
如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )| A. | $\frac{ED}{BC}$=$\frac{EF}{FB}$ | B. | $\frac{DE}{AD}$=$\frac{DF}{AB}$ | C. | $\frac{BC}{DE}$=$\frac{CF}{DF}$ | D. | $\frac{BF}{BE}$=$\frac{BC}{AE}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
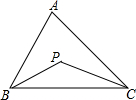 如图,在三角形ABC中,∠ABC与∠ACB的平分线交于点P,设∠A=x°,∠BPC=y°,当∠A变化时,求y与x之间的函数关系式.并判断y是不是x的一次函数.
如图,在三角形ABC中,∠ABC与∠ACB的平分线交于点P,设∠A=x°,∠BPC=y°,当∠A变化时,求y与x之间的函数关系式.并判断y是不是x的一次函数.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\frac{1}{3}$ | C. | -$\frac{2}{3}$ | D. | -$\frac{4}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | 8 | C. | $\frac{1}{6}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com