已知关于x的一元二次方程x2+px+q+1=0的一个实数根为2.
(1)用含p的代数式表示q;
(2)求证:抛物线y=x2+px+q与x轴有两个交点;
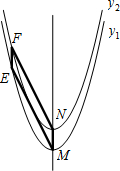
(3)设抛物线y1=x2+px+q的顶点为M,与y轴的交点为E,抛物线y2=x2+px+q+1顶点为N,与y轴的交点为F,若四边形FEMN的面积等于2,求p的值.
解:(1)∵关于x的一元二次方程x
2+px+q+1=0的一个实数根为 2,
∴2
2+2p+q+1=0.…
整理,得 q=-2p-5. …
(2)∵△=p
2-4(q+1)=p
2+4(2p+5)=p
2+8p+20=(p+4)
2+4,
无论p取任何实数,都有(p+4)
2≥0,
∴无论p取任何实数,都有 (p+4)
2+4>0.
∴△>0. …
∴抛物线y=x
2+px+q与x轴有两个交点.…
(3)∵抛物线
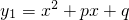
与抛物线
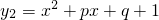
的对称轴相同,都为直线
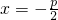
,且开口大小相同,
抛物线
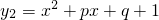
可由抛物线
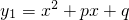
沿y轴方向向上平移一个单位得到,
(如图5所示,省略了x轴、y轴)
∴EF∥MN,EF=MN=1.
∴四边形FEMN是平行四边形. …
由题意得
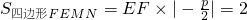
.
解得p=±4.…
分析:(1)把x=2代入方程x
2+px+q+1=0中,可得出p、q的关系式;
(2)用判别式进行判断,同时,把(1)的关系式代入,利用配方法证明△>0即可;
(3)由两抛物线的解析式可知,抛物线y
2可由抛物线y
1向上平移1个单位得到,利用平移的性质证明四边形FEMN为平行四边形,根据平行四边形的面积公式列方程求p的值.
点评:本题考查了二次函数的综合运用.关键是把二次函数与一元二次方程结合解题,形数结合,通过观察两抛物线解析式,得出平移的关系.

 解:(1)∵关于x的一元二次方程x2+px+q+1=0的一个实数根为 2,
解:(1)∵关于x的一元二次方程x2+px+q+1=0的一个实数根为 2,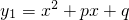 与抛物线
与抛物线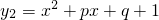
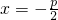 ,且开口大小相同,
,且开口大小相同,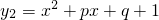 可由抛物线
可由抛物线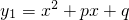
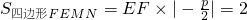 .
.

 .
. .
.