
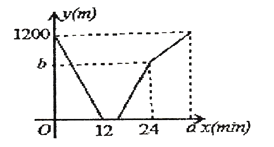
【题目】甲、乙两人分别从A、B两地同时出发,相向而行,匀速前往B地、A地,两人相遇时停留了4min,又各自按原速前往目的地,甲、乙两人之间的距离y(m)与甲所用时间x(min) 之间的函数关系如图所示.有下列说法: ①A、B之间的距离为1200m;②甲行走的速度是乙的1.5倍;③![]() ;④
;④![]() .以上结论正确的有( )
.以上结论正确的有( )
A.①④B.①②③C.①③④D.①②④
【答案】A
【解析】
①由x=0时y=1200,可得出A、B之间的距离为1200m,结论①正确;②根据速度=路程÷时间可求出乙的速度,再根据甲的速度=路程÷时间-乙的速度可求出甲的速度,二者相除即可得出乙行走的速度是甲的1.5倍,结论②正确;③根据路程=二者速度和×运动时间,即可求出b=800,结论③错误;④根据甲走完全程所需时间=两地间的距离÷甲的速度+4,即可求出a=34,结论④正确.综上即可得出结论.
①当x=0时,y=1200,
∴A、B之间的距离为1200m,结论①正确;
②乙的速度为1200÷(244)=60(m/min),
甲的速度为1200÷1260=40(m/min),
60÷40=1.5,
∴乙行走的速度是甲的1.5倍,结论②错误;
③b=(60+40)×(24412)=800,结论③错误;
④a=1200÷40+4=34,结论④正确。
故选A.


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.

(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
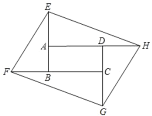
【题目】如图,将矩形ABCD的四边BA,CB,DC,AD分别延长至点EF,G,H,使得AE=BF=CG=DH.已知AB=1,BC=2,∠BEF=30°,则tan∠AEH的值为( )
A.2B.![]() C.
C.![]() ﹣1D.
﹣1D.![]() +1
+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图:分别以△ABC的各边为边,在BC边的同侧作等边三角形ABE、等边三角形CBD和等边三角形ACF,连结DE,DF.

(1)试说明四边形DEAF为平行四边形.
(2)当△ABC满足什么条件时,四边形DEAF为矩形?并说明理由;
(3)当△ABC满足什么条件时,四边形DEAF为菱形.直接写出答案 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标![]() 中,正比例函数
中,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象经过点
的图象经过点![]() .
.
(![]() )分别求这两个函数的表达式.
)分别求这两个函数的表达式.
(![]() )将直线
)将直线![]() 向上平移
向上平移![]() 个单位长度后与
个单位长度后与![]() 轴交于点
轴交于点![]() ,与反比例函数图象在第四象限内的交点为
,与反比例函数图象在第四象限内的交点为![]() ,连接
,连接![]() 、
、![]() ,求点
,求点![]() 的坐标及
的坐标及![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市预测某饮料有发展前途,用1600元购进一批饮料,面市后果然供不应求,又用6000元购进这批饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若二次购进饮料按同一价格销售,两批全部售完后,获利不少于1200元,那么销售单价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 图象的一部分如图所示,给出以下结论:
图象的一部分如图所示,给出以下结论:![]() ;
;![]() 当
当![]() 时,函数有最大值;
时,函数有最大值;![]() 方程
方程![]() 的解是
的解是![]() ,
,![]() ;
;![]() ,其中结论错误的个数是
,其中结论错误的个数是![]()
![]()
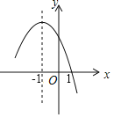
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市正在开展“食品安全城市”创建活动,为了解学生对食品安全知识的了解情况,学校从2019年1月﹣5月等月随机抽取了部分学生进行问卷调查(被调查学生每人只能选一项),将调查站果按照“A非常了解、B了解、C了解较少、D不了解”四类情况分别选行统计,并绘制成图1、图2两幅统计图、根据统计图提供的信息解答下列问题:
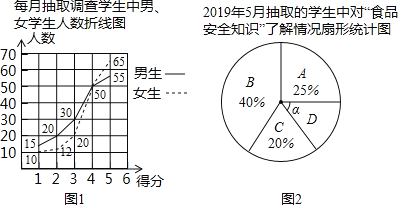
(1) 月抽取的调查人数最少: 月抽取的调查人数中男生、女生人数相等;
(2)求图2中“D不了解”在扇形图中所占的圆心角α的度数:
(3)若该校2019年5月份在校学生3600名,请你估计对食品安全知识“A非常了解和B了解”的学生总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
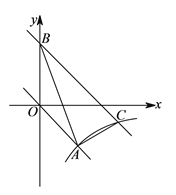
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,抛物线
两点,抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴另一交点为
轴另一交点为![]() ,顶点为
,顶点为![]() .
.
(1)求抛物线的解析式;
(2)在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的值最小,求
的值最小,求![]() 的最小值;
的最小值;
(3)在抛物线的对称轴上是否存在一点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com