
【题目】某市正在开展“食品安全城市”创建活动,为了解学生对食品安全知识的了解情况,学校从2019年1月﹣5月等月随机抽取了部分学生进行问卷调查(被调查学生每人只能选一项),将调查站果按照“A非常了解、B了解、C了解较少、D不了解”四类情况分别选行统计,并绘制成图1、图2两幅统计图、根据统计图提供的信息解答下列问题:
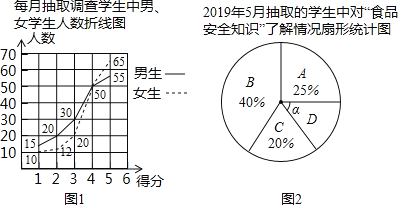
(1) 月抽取的调查人数最少: 月抽取的调查人数中男生、女生人数相等;
(2)求图2中“D不了解”在扇形图中所占的圆心角α的度数:
(3)若该校2019年5月份在校学生3600名,请你估计对食品安全知识“A非常了解和B了解”的学生总人数.
【答案】(1)1,4;(2)54°;(3)2340人.
【解析】
(1)依据折线统计图中的数据,即可得到结果;(2)扇形圆心角的度数=部分占总体的百分比×360°,由此即可解答;(3)用总人数乘以对食品安全知识“A非常了解和B了解”的学生占总人数的百分比即可求解.
(1)由题可得,1月抽取的调查人数最少为25人;4月抽取的调查人数中男生、女生人数相等,均为50人;
故答案为:1,4;
(2)“D不了解”在扇形图中所占的圆心角α的度数:360°×(1﹣25%﹣40%﹣20%)=54°;
(3)对食品安全知识“A非常了解和B了解”的学生总人数为3600×(40%+25%)=2340(人).


 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,⊙C的半径为r,给出如下定义:若点P的横、纵坐标均为整数,且到圆心C的距离d≤r,则称P为⊙C 的关联整点.
(1)当⊙O的半径r=2时,在点D(2,-2),E(-1,0),F(0,2)中,为⊙O的关联整点的是 ;
(2)若直线![]() 上存在⊙O的关联整点,且不超过7个,求r的取值范围;
上存在⊙O的关联整点,且不超过7个,求r的取值范围;
(3)⊙C的圆心在x轴上,半径为2,若直线![]() 上存在⊙C的关联整点,求圆心C的横坐标t的取值范围.
上存在⊙C的关联整点,求圆心C的横坐标t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
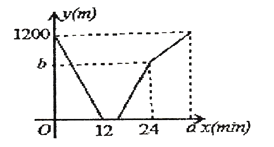
【题目】甲、乙两人分别从A、B两地同时出发,相向而行,匀速前往B地、A地,两人相遇时停留了4min,又各自按原速前往目的地,甲、乙两人之间的距离y(m)与甲所用时间x(min) 之间的函数关系如图所示.有下列说法: ①A、B之间的距离为1200m;②甲行走的速度是乙的1.5倍;③![]() ;④
;④![]() .以上结论正确的有( )
.以上结论正确的有( )
A.①④B.①②③C.①③④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
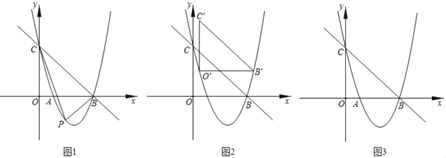
【题目】如图1,抛物线y=ax2﹣![]() x+c交x轴于A,B两点,交y轴于点C.直线y=﹣
x+c交x轴于A,B两点,交y轴于点C.直线y=﹣![]() x+3经过点B,C.
x+3经过点B,C.
(1)求抛物线的解析式;
(2)若点P为直线BC下方的抛物线上一动点(不与点B,C重合),则△PBC的面积能够等于△BOC的面积吗?若能,求出相应的点P的坐标;若不能,请说明理由;
(3)如图2,现把△BOC平移至如图所示的位置,此时三角形水平方向一边的两个端点点O′与点B′都在抛物线上,称点O′和点B′为△BOC在抛物线上的一“卡点对”;如果把△BOC旋转一定角度,使得其余边位于水平方向然后平移,能够得到这个三角形在抛物线上新的“卡点对”.请直接写出△BOC在已知抛物线上所有“卡点对”的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国科学技术馆有“圆与非圆”展品,涉及了“等宽曲线”的知识.因为圆的任何一对平行切线的距离总是相等的,所以圆是“等宽曲线”.除了例以外,还有一些几何图形也是“等宽曲线”,如勒洛只角形(图1),它是分别以等边三角形的征个顶点为圆心,以边长为半径,在另两个顶点间画一段圆弧.三段圆弧围成的曲边三角形.图2是等宽的勒洛三角形和圆.
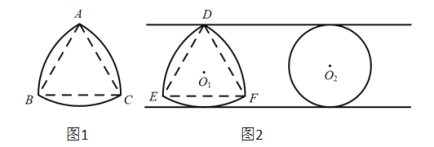
下列说法中错误的是( )
A.勒洛三角形是轴对称图形
B.图1中,点A到![]() 上任意一点的距离都相等
上任意一点的距离都相等
C.图2中,勒洛三角形上任意一点到等边三角形DEF的中心![]() 的距离都相等
的距离都相等
D.图2中,勒洛三角形的周长与圆的周长相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:一组邻边相等且对角互补的四边形叫做“邻等对补四边形”
如图1,四边形ABCD中,AB=BC,∠B+∠D=180°(或∠A+∠C=180°),则四边形ABCD叫做“邻等对补四边形”.
概念理解
(1)在以下四种图形中:①平行四边形,②菱形,③矩形,④正方形;一定是“邻等对补四边形”的是 ;(填写序号)
(2)如图2,点A、B、C是网格中格点,请找出两个格点P1,P2,连接P1A、P1C,P2A、P2C画出四边形P1ABC,P2ABC,使四边形P1ABC,P2ABC均为“邻等对补四边形”.
性质证明
(3)如图1,四边形ABCD中,AB=BC,∠A+∠C=180°,连接BD,求证:BD平分∠ADC.
知识运用
(4)如图3,在“邻等对补四边形”ABCD中,满足AB=AD,AB+BC=6,∠ADC=60°时,若2≤BC<3,求四边形ABCD的面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+4交y轴于点A,并经过B(4,4)和C(6,0)两点,点D的坐标为(4,0),连接AD,BC,点F从点O出发,以每秒1个单位长度的速度沿线段OC方向运动,到达点C后停止运动:点M同时从点D出发以每秒1个单位长度的速度沿x轴正方向运动,当点F停止时点M也停止运动.设点F的运动时间为t秒,过点F作AB的垂线EF交直线AB于点E,交AD于点H.

(1)求抛物线的解析式;
(2)以线段EH为斜边向右作等腰直角△EHG,当点G落在第一象限内的抛物线上时,求出t的值;
(3)设△EFM与四边形ADCB重合时的面积为S,请直接写出S与t的函数关系式与相应的自变量t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c过等腰Rt△OAB的A,B两点,点B在点A的右侧,直角顶点A(0,3).
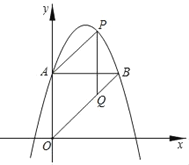
(1)求b,c的值.
(2)P是AB上方抛物线上的一点,作PQ⊥AB交OB于点Q,连接AP,是否存在点P,使四边形APQO是平行四边形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,∠A=60°,点O为AB上一点,且3AO=AB,以OA为半径作半圆O,交AC于点D,AB于点E,DE与OC相交于F.
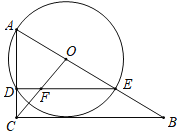
(1)求证:CB与⊙O相切;
(2)若AB=6,求DF的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com