
【题目】定义:一组邻边相等且对角互补的四边形叫做“邻等对补四边形”
如图1,四边形ABCD中,AB=BC,∠B+∠D=180°(或∠A+∠C=180°),则四边形ABCD叫做“邻等对补四边形”.
概念理解
(1)在以下四种图形中:①平行四边形,②菱形,③矩形,④正方形;一定是“邻等对补四边形”的是 ;(填写序号)
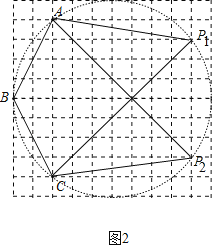
(2)如图2,点A、B、C是网格中格点,请找出两个格点P1,P2,连接P1A、P1C,P2A、P2C画出四边形P1ABC,P2ABC,使四边形P1ABC,P2ABC均为“邻等对补四边形”.
性质证明
(3)如图1,四边形ABCD中,AB=BC,∠A+∠C=180°,连接BD,求证:BD平分∠ADC.
知识运用
(4)如图3,在“邻等对补四边形”ABCD中,满足AB=AD,AB+BC=6,∠ADC=60°时,若2≤BC<3,求四边形ABCD的面积的最大值.

【答案】(1)④;(2)详见解析;(3)详见解析;(4)四边形ABCD的面积的最大值最大值为8![]() .
.
【解析】
(1)根据“邻等对补四边形”的定义即可判断;(2)如图作△ABC的外接圆,图中点P1,P2即为所求(答案不唯一,在直线AC的右侧圆上的格点,即可满足条件);(3)如图1中,连接AC,BD.证明A,B,C,D四点共圆,利用圆周角定理即可解决问题;(4)如图3中,延长CB到H,使得BH=BA,连接AH,AC,作CE⊥AD于E,CF⊥AH于F,作AK⊥BH于K.设BC=x.构建二次函数,利用二次函数的性质即可解决问题.
(1)根据“邻等对补四边形”的定义,正方形一定是“邻等对补四边形”.
故答案为:④.
(2)如图2中,作△ABC的外接圆,图中点P1,P2即为所求(答案不唯一)
(3)如图1中,连接AC,BD.

∵∠BAD+∠BCD=180°,
∴A,B,C,D四点共圆,
∴BA=BC,
∴![]() ,
,
∴∠ADB=∠BDC,
∴BD平分∠ADC.
(4)如图3中,延长CB到H,使得BH=BA,连接AH,AC,作CE⊥AD于E,CF⊥AH于F,作AK⊥BH于K.设BC=x.

∵∠ADC+∠ABC=180°,∠ADC=60°,
∴∠ABC=120°,
∴∠ABH=60°,
∵BA=BH,
∴△ABH是等边三角形,
∴∠H=60°,
∴∠H=∠D,
由(2)可知.AC平分∠BCD,
∴∠ACH=∠ACD,
∵AC=AC,
∴△ACH≌△ACD,
∴∠CAD=∠CAH,
∵CE⊥AD,CF⊥AH,
∴CE=CF,
∵BH+BC=AB+BC=6,
∴CF=CE=CHsin60°=3![]() ,AK=HKtan60°=
,AK=HKtan60°=![]() (6﹣x),
(6﹣x),
∴S四边形ABCD=S△ADC+S△ACB=![]() (6﹣x)3
(6﹣x)3![]() +
+![]() x
x![]() (6﹣x)=﹣
(6﹣x)=﹣![]() x2+9
x2+9![]() ,
,
∵2≤x<3,
∴x=2时,S有最大值,最大值S=8![]() ,
,


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
【题目】自2016年共享单车上市以来,给人们的出行提供了了便利,受到了广大市民的青睐,某公司为了了解员工上下班回家的路线(设路程为x公里)情况,随机抽取了若干名员工进行了问卷调查,现将这些员工的谓查结果分为四个等级,A:0≤x≤3、B:3<x≤6、C:6<x≤9、D:x>9,并将调查结果绘制成如下两个不完整的统计图。
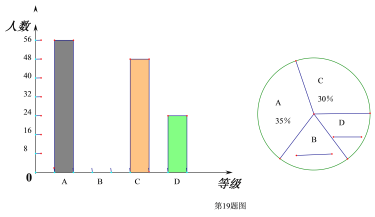
(1)补全上面的条形统计图和扇形统计图中的B D ;
(2)所抽取员工下班路程的中位数落在等级 (填字母)
(3)若该公司有900名员工,为了方便员工上下班,在高峰期时规定路程在6公里以上可优先选择共享单车下斑,请你估算该公司有多少人可以优先选择共享单车。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市预测某饮料有发展前途,用1600元购进一批饮料,面市后果然供不应求,又用6000元购进这批饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若二次购进饮料按同一价格销售,两批全部售完后,获利不少于1200元,那么销售单价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
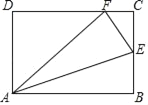
【题目】如图所示,将矩形ABCD沿AE折叠得到△AFE,且点B恰好与DC上的点F重合.
(1)求证:△ADF∽△FCE;
(2)若tan∠CEF=2,求tan∠AEB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市正在开展“食品安全城市”创建活动,为了解学生对食品安全知识的了解情况,学校从2019年1月﹣5月等月随机抽取了部分学生进行问卷调查(被调查学生每人只能选一项),将调查站果按照“A非常了解、B了解、C了解较少、D不了解”四类情况分别选行统计,并绘制成图1、图2两幅统计图、根据统计图提供的信息解答下列问题:
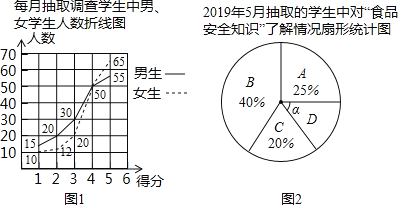
(1) 月抽取的调查人数最少: 月抽取的调查人数中男生、女生人数相等;
(2)求图2中“D不了解”在扇形图中所占的圆心角α的度数:
(3)若该校2019年5月份在校学生3600名,请你估计对食品安全知识“A非常了解和B了解”的学生总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
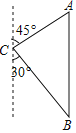
【题目】如图,一艘海轮位于灯塔C的北偏东45方向,距离灯塔100海里的A处,它沿正南方向航行一段时间后,到达位于灯塔C的南偏东30°方向上的B处,求此时船距灯塔的距离(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,结果取整数).
≈1.732,结果取整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,我们不妨将横坐标,纵坐标均为整数的点称之为“中国结”。
(1)求函数y=![]() x+2的图像上所有“中国结”的坐标;
x+2的图像上所有“中国结”的坐标;
(2)求函数y=![]() (k≠0,k为常数)的图像上有且只有两个“中国结”,试求出常数k的值与相应“中国结”的坐标;
(k≠0,k为常数)的图像上有且只有两个“中国结”,试求出常数k的值与相应“中国结”的坐标;
(3)若二次函数y=![]() (k为常数)的图像与x轴相交得到两个不同的“中国结”,试问该函数的图像与x轴所围成的平面图形中(含边界),一共包含有多少个“中国结”?
(k为常数)的图像与x轴相交得到两个不同的“中国结”,试问该函数的图像与x轴所围成的平面图形中(含边界),一共包含有多少个“中国结”?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1、图2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AC的两个端点均在小正方形的顶点上.
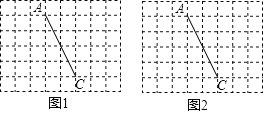
(1)在图1中画一个以线段AC为对角线、周长为20的四边形ABCD,且点B和点D均在小正方形的顶点上,并求出BD的长;
(2)在图2中画一个以线段AC为对角线、面积为10的四边形ABCD,且点B和点D均在小正方形的顶点上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com