
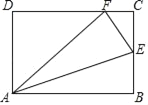
【题目】如图所示,将矩形ABCD沿AE折叠得到△AFE,且点B恰好与DC上的点F重合.
(1)求证:△ADF∽△FCE;
(2)若tan∠CEF=2,求tan∠AEB的值.
【答案】(1)见解析;(2)tan∠AEB=![]() .
.
【解析】
(1)因为△AEF是由△AEB翻折得到,推出∠AFB=∠B=90°,推出∠AFD+∠EFC=90°,∠EFC+∠FEC=90°,推出∠AFD=∠FEC,由此即可证明.
(2))由tan∠FEC![]() 2,推出CF=2EC,设EC=a,则FC=2a,EF=EB
2,推出CF=2EC,设EC=a,则FC=2a,EF=EB![]() a,由△ADF∽△FCE,得
a,由△ADF∽△FCE,得![]() ,即
,即![]() ,推出DF
,推出DF![]() a,根据tan∠AEB
a,根据tan∠AEB![]() 计算即可.
计算即可.
(1)∵四边形ABCD是矩形,∴AB=DC,AD=BC,∠D=∠C=∠B=90°.
∵△AEF是由△AEB翻折得到,∴∠AFB=∠B=90°,∴∠AFD+∠EFC=90°,∠EFC+∠FEC=90°,∴∠AFD=∠FEC.
∵∠D=∠C,∴△ADF∽△FCE.
(2)∵tan∠FEC![]() 2,∴CF=2EC,设EC=a,则FC=2a,EF=EB
2,∴CF=2EC,设EC=a,则FC=2a,EF=EB![]() a.
a.
∵△ADF∽△FCE,∴![]() ,∴
,∴![]() ,∴DF
,∴DF![]() a,∴AB=CD=DF+CF
a,∴AB=CD=DF+CF![]() a,∴tan∠AEB
a,∴tan∠AEB![]() .
.


科目:初中数学 来源: 题型:
【题目】某农场去年种植了10亩地的南瓜,亩产量为2000kg,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜,设南瓜种植面积的增长率为x.
(1)则今年南瓜的种植面积为 亩;(用含x的代数式表示)
(2)如果今年南瓜亩产量的增长率是种植面积的增长率的![]() ,今年南瓜的总产量为60000kg,求南瓜亩产量的增长率.
,今年南瓜的总产量为60000kg,求南瓜亩产量的增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
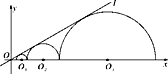
【题目】如图,圆心都在x轴正半轴上的半圆O1,半圆O2,…,半圆On与直线l相切.设半圆O1,半圆O2,…,半圆On的半径分别是r1,r2,…,rn,则当直线l与x轴所成锐角为30°,且r1=1时,r2018=_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:(1)sin2 1°+sin2 2°+sin2 3°+…+sin2 87°+sin2 88°+sin2 89°
(2)sin2 66°-tan54°tan36°+sin2 24°+sin230°+cos230°+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论:
①△BDE∽△DPE;②![]() =
=![]() ;③DP2=PHPB;④tan∠DBE=2﹣
;③DP2=PHPB;④tan∠DBE=2﹣![]() .
.
其中正确的是( )
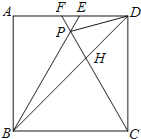
A.①②③④ B.①②④ C.②③④ D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图像如图所示,并且关于x的一元二次方程ax2+bx+c –m=0有两个实数根,下列结论:①b2-4ac>0;②abc>0;③![]() ;④
;④![]() ,其中正确的个数有( )
,其中正确的个数有( )
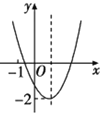
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形OABC的顶点A在y轴正半轴上,顶点C在x轴正半轴上,抛物线![]() (a<0)的顶点为D,且经过点A、B.若△ABD为等腰直角三角形,则a的值为___________.
(a<0)的顶点为D,且经过点A、B.若△ABD为等腰直角三角形,则a的值为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某水库上游有一单孔抛物线型拱桥,它的跨度AB为100米.最低水位(与AB在同一平面)时桥面CD距离水面25米,桥拱两端有两根25米高的水泥柱BC和AD,中间等距离竖立9根钢柱支撑桥面,拱顶正上方的钢柱EF长5米.
(1)建立适当的直角坐标系,求抛物线型桥拱的解析式;
(2)在最低水位时,能并排通过两艘宽28米,高16米的游轮吗?(假设两游轮之间的安全间距为4米)
(3)由于下游水库蓄水及雨季影响导致水位上涨,水位最高时比最低水位高出13米,请问最高水位时没在水面以下的钢柱总长为多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店将进价为8元的商品按每件10元出售,每天可销售200件,现商家采用提高售价,减少进货量的方法增加利润,如果这种商品每件涨0.5元,其销量就会减少10件,那么要使利润为640元,需将售价定为( )
A. 16元 B. 12元 C. 16元或12元 D. 14元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com