练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】图1、图2是两张形状和大小完全相同的方格纸，方格纸中每个小正方形的边长均为1，线段AC的两个端点均在小正方形的顶点上．

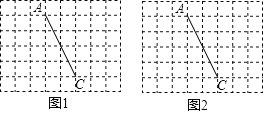
    （1）在图1中画一个以线段AC为对角线、周长为20的四边形ABCD，且点B和点D均在小正方形的顶点上，并求出BD的长；

    （2）在图2中画一个以线段AC为对角线、面积为10的四边形ABCD，且点B和点D均在小正方形的顶点上．

    【答案】（1）如图1所示，四边形ABCD即为所求，见解析；BD＝4；（2）如图2，四边形ABCD即为所求．见解析.

    【解析】

    （1）作一边长为5的菱形即可得；

    （2）作一边长为5、且这条边上的高为2的平行四边形可得．

    （1）如图1所示，四边形ABCD即为所求，

    BD＝＝4；

    （2）如图2，四边形ABCD即为所求．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】定义：一组邻边相等且对角互补的四边形叫做“邻等对补四边形”

    如图1，四边形ABCD中，AB＝BC，∠B+∠D＝180°（或∠A+∠C＝180°），则四边形ABCD叫做“邻等对补四边形”．

    概念理解

    （1）在以下四种图形中：①平行四边形，②菱形，③矩形，④正方形；一定是“邻等对补四边形”的是　 　；（填写序号）

    （2）如图2，点A、B、C是网格中格点，请找出两个格点P1，P2，连接P1A、P1C，P2A、P2C画出四边形P1ABC，P2ABC，使四边形P1ABC，P2ABC均为“邻等对补四边形”．

    性质证明

    （3）如图1，四边形ABCD中，AB＝BC，∠A+∠C＝180°，连接BD，求证：BD平分∠ADC．

    知识运用

    （4）如图3，在“邻等对补四边形”ABCD中，满足AB＝AD，AB+BC＝6，∠ADC＝60°时，若2≤BC＜3，求四边形ABCD的面积的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在数学课上，老师提出利用尺规作图完成下面问题：已知：△ABC是⊙O的内接三角形．求作：△ABC中∠BAC的平分线．

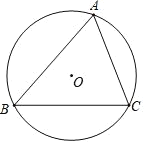
    小明的作法如下：

    （1）作BC边的垂直平分线DE，交BC于点D，交弧BC于点E；

    （2）连接AE，交BC边于点F；则线段AF为所求△ABC中∠BAC的平分线．根据小明设计的尺规作图过程，

    ①在图中补全图形（尺规作图，保留作图痕迹）；

    ②完成下面的证明．

    证明：∵OB＝OC，DE是线段BC的垂直平分线

    ∴圆心O在直线DE上（　 　）．

    ∵DE⊥BC，

    ∴（　 　）．

    ∴∠BAE＝∠CAE（　 　），

    ∴线段AF为所求△ABC中∠BAC的平分线．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，BD为菱形ABCD的一条对角线，E、F在BD上，且四边形ACEF为矩形，若EF=BD，则 的值为（　　）

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，∠ACB=90°，∠A=60°，点O为AB上一点，且3AO=AB，以OA为半径作半圆O，交AC于点D，AB于点E，DE与OC相交于F．

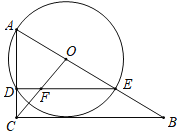
    （1）求证：CB与⊙O相切；

    （2）若AB=6，求DF的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

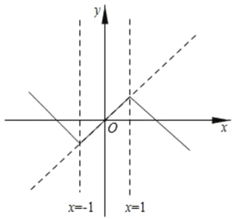
    【题目】在平面直角坐标系中，某个函数图象上任意两点的坐标分别为（﹣t，y1）和（t，y2）（其中t为常数且t＞0），将x＜﹣t的部分沿直线y＝y1翻折，翻折后的图象记为G1；将x＞t的部分沿直线y＝y2翻折，翻折后的图象记为G2，将G1和G2及原函数图象剩余的部分组成新的图象G．

    例如：如图，当t＝1时，原函数y＝x，图象G所对应的函数关系式为y＝．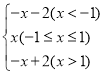

    （1）当t＝时，原函数为y＝x+1，图象G与坐标轴的交点坐标是　 ．

    （2）当t＝时，原函数为y＝x2﹣2x

    ①图象G所对应的函数值y随x的增大而减小时，x的取值范围是　 ．

    ②图象G所对应的函数是否有最大值，如果有，请求出最大值；如果没有，请说明理由．

    （3）对应函数y＝x2﹣2nx+n2﹣3（n为常数）．

    ①n＝﹣1时，若图象G与直线y＝2恰好有两个交点，求t的取值范围．

    ②当t＝2时，若图象G在n2﹣2≤x≤n2﹣1上的函数值y随x的增大而减小，直接写出n的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

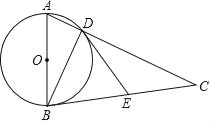
    【题目】如图，在锐角△ABC中，以AB为直径的⊙O交AC于点D，过点D作⊙O的切线DE交边BC于点E，连结BD．

    （1）求证：∠ABD＝∠CDE．

    （2）若AC＝28，tanA＝2，AD：DC＝1：3，求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

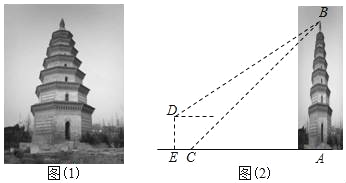
    【题目】如图（1），在豫西南邓州市大十字街西南方，耸立着一座古老建筑﹣福胜寺梵塔，建于北宋天圣十年（公元1032年），当地民谚云：“邓州有座塔，离天一丈八．”学完了三角函数知识后，某校“数学社团”的刘明和王华决定用自己学到的知识测量“福胜寺梵塔”的高度．如图（2），刘明在点C处测得塔顶B的仰角为45°，王华在高台上的点D处测得塔顶B的仰角为40°，若高台DE高为5米，点D到点C的水平距离EC为1.3米，且A、C、E三点共线，求该塔AB的高度．（参考数据：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84，结果保留整数）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校初三（3）班的同学踊跃为“雅安芦山地震”捐款，根据捐款情况（捐款数为正数）制作以下统计图表，但生活委员不小心把墨水滴在统计表上，部分数据看不清楚。

    （1）全班有多少人捐款？

    （2）如果捐款0～20元的人数在扇形统计图中所占的圆心角为72°，那么捐款21～40元的有多少人？

    查看答案和解析>>

    同步练习册答案