
【题目】在平面直角坐标系中,某个函数图象上任意两点的坐标分别为(﹣t,y1)和(t,y2)(其中t为常数且t>0),将x<﹣t的部分沿直线y=y1翻折,翻折后的图象记为G1;将x>t的部分沿直线y=y2翻折,翻折后的图象记为G2,将G1和G2及原函数图象剩余的部分组成新的图象G.
例如:如图,当t=1时,原函数y=x,图象G所对应的函数关系式为y=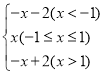 .
.
(1)当t=![]() 时,原函数为y=x+1,图象G与坐标轴的交点坐标是 .
时,原函数为y=x+1,图象G与坐标轴的交点坐标是 .
(2)当t=![]() 时,原函数为y=x2﹣2x
时,原函数为y=x2﹣2x
①图象G所对应的函数值y随x的增大而减小时,x的取值范围是 .
②图象G所对应的函数是否有最大值,如果有,请求出最大值;如果没有,请说明理由.
(3)对应函数y=x2﹣2nx+n2﹣3(n为常数).
①n=﹣1时,若图象G与直线y=2恰好有两个交点,求t的取值范围.
②当t=2时,若图象G在n2﹣2≤x≤n2﹣1上的函数值y随x的增大而减小,直接写出n的取值范围.
【答案】(1)(2,0);(2)①﹣![]() ≤x≤1或x≥
≤x≤1或x≥![]() ;②图象G所对应的函数有最大值为
;②图象G所对应的函数有最大值为![]() ;(3)①
;(3)①![]() ;②n≤
;②n≤![]() 或n≥
或n≥![]() .
.
【解析】
(1)根据题意分别求出翻转之后部分的表达式及自变量的取值范围,将y=0代入,求出x值,即可求出图象G与坐标轴的交点坐标;
(2)画出函数草图,求出翻转点和函数顶点的坐标,①根据图象的增减性可求出y随x的增大而减小时,x的取值范围,②根据图象很容易计算出函数最大值;
(3)①将n=﹣1代入到函数中求出原函数的表达式,计算y=2时,x的值.据(2)中的图象,函数与y=2恰好有两个交点时t大于右边交点的横坐标且-t大于左边交点的横坐标,据此求解.
②画出函数草图,分别计算函数左边的翻转点A,右边的翻转点C,函数的顶点B的横坐标(可用含n的代数式表示),根据函数草图以及题意列出关于n的不等式求解即可.
(1)当x=![]() 时,y=
时,y=![]() ,
,
当x≥![]() 时,翻折后函数的表达式为:y=﹣x+b,将点(
时,翻折后函数的表达式为:y=﹣x+b,将点(![]() ,
,![]() )坐标代入上式并解得:
)坐标代入上式并解得:
翻折后函数的表达式为:y=﹣x+2,
当y=0时,x=2,即函数与x轴交点坐标为:(2,0);
同理沿x=﹣![]() 翻折后当
翻折后当![]() 时函数的表达式为:y=﹣x,
时函数的表达式为:y=﹣x,
函数与x轴交点坐标为:(0,0),因为![]() 所以舍去.
所以舍去.
故答案为:(2,0);
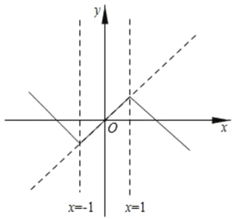
(2)当t=![]() 时,由函数为y=x2﹣2x构建的新函数G的图象,如下图所示:
时,由函数为y=x2﹣2x构建的新函数G的图象,如下图所示:
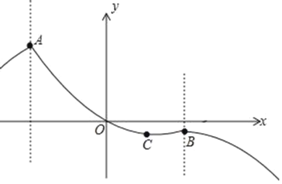
点A、B分别是t=﹣![]() 、t=
、t=![]() 的两个翻折点,点C是抛物线原顶点,
的两个翻折点,点C是抛物线原顶点,
则点A、B、C的横坐标分别为﹣![]() 、1、
、1、![]() ,
,
①函数值y随x的增大而减小时,﹣![]() ≤x≤1或x≥
≤x≤1或x≥![]() ,
,
故答案为:﹣![]() ≤x≤1或x≥
≤x≤1或x≥![]() ;
;
②函数在点A处取得最大值,
x=﹣![]() ,y=(﹣
,y=(﹣![]() )2﹣2×(﹣
)2﹣2×(﹣![]() )=
)=![]() ,
,
答:图象G所对应的函数有最大值为![]() ;
;
(3)n=﹣1时,y=x2+2x﹣2,
①参考(2)中的图象知:
当y=2时,y=x2+2x﹣2=2,
解得:x=﹣1±![]() ,
,
若图象G与直线y=2恰好有两个交点,则t>![]() ﹣1且-t>
﹣1且-t>![]() ,
,
所以![]() ;
;
②函数的对称轴为:x=n,
令y=x2﹣2nx+n2﹣3=0,则x=n±![]() ,
,
当t=2时,点A、B、C的横坐标分别为:﹣2,n,2,
当x=n在y轴左侧时,(n≤0),
此时原函数与x轴的交点坐标(n+![]() ,0)在x=2的左侧,如下图所示,
,0)在x=2的左侧,如下图所示,

则函数在AB段和点C右侧,
故:﹣2≤x≤n,即:在﹣2≤n2﹣2≤x≤n2﹣1≤n,
解得:n≤![]() ;
;
当x=n在y轴右侧时,(n≥0),
同理可得:n≥![]() ;
;
综上:n≤![]() 或n≥
或n≥![]() .
.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
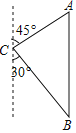
【题目】如图,一艘海轮位于灯塔C的北偏东45方向,距离灯塔100海里的A处,它沿正南方向航行一段时间后,到达位于灯塔C的南偏东30°方向上的B处,求此时船距灯塔的距离(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,结果取整数).
≈1.732,结果取整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,△ABC中AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B、M两点的⊙O交BC于G,交AB于点F,FB恰为⊙O的直径.
(1)求证:AE与⊙O相切;
(2)当BC=6,cosC=![]() ,求⊙O的直径.
,求⊙O的直径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了美化环境,建设最美西安,我市准备在一个广场上种植甲、乙两种花卉,经市场调查,甲种花卉的种植费用为y(元)与种植面积x(m2)之间的函数关系如图所示,乙种花卉的种植费用为100元/m2.
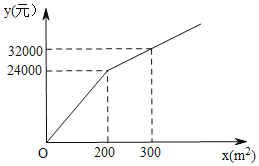
(1)求y与x之间的函数关系式;
(2)广场上甲、乙两种花卉的种植面积共1200m2,若甲种花卉的种植面积不少于200m2,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植费用最少?最少费用为多少元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1、图2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AC的两个端点均在小正方形的顶点上.
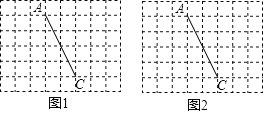
(1)在图1中画一个以线段AC为对角线、周长为20的四边形ABCD,且点B和点D均在小正方形的顶点上,并求出BD的长;
(2)在图2中画一个以线段AC为对角线、面积为10的四边形ABCD,且点B和点D均在小正方形的顶点上.
查看答案和解析>>
科目:初中数学 来源: 题型:
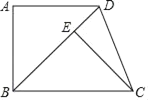
【题目】如图,在四边形ABCD中,AD∥BC,∠A=90°,过点C作CE⊥BD交BD于点E,且CE=AB.
(1)求证:△ABD≌△ECB;
(2)若AB=AD,求∠ADC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级男生1000米跑的水平,从中随机抽取部分男生进行测试,并把测试成绩分为D、C、B、A四个等次绘制成如图所示的不完整的统计图,请你依图解答下列问题:
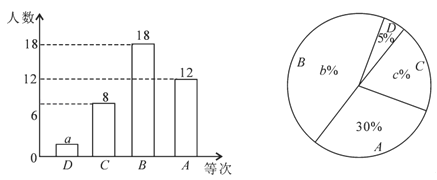
(1)a= ,b= ,c= ;
(2)扇形统计图中表示C等次的扇形所对的圆心角的度数为 度;
(3)学校决定从A等次的甲、乙、丙、丁四名男生中,随机选取两名男生参加全市中学生1000米跑比赛,请用列表法或画树状图法,求甲、乙两名男生同时被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学计划购买A型和B型课桌凳共200套,经招标,购买一套A型课桌凳比购买一套B型课桌凳少用40元,,且购买4套A型和6套B型课桌凳共需1820元。
(1)求购买一套A型课桌凳和一套B型课桌凳各需多少元?
(2)学校根据实际情况,要求购买这两种课桌凳总费用不能超过40880元,并且购买A型课桌凳的数量不能超过B型课桌凳的![]() ,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
查看答案和解析>>
科目:初中数学 来源: 题型:
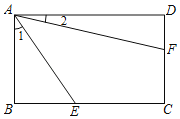
【题目】如图,矩形ABCD长与宽的比为5:3,点E、F分别在边BC、CD上,tan∠1=![]() ,tan∠2=
,tan∠2=![]() ,则cos(∠1+∠2)的值为( )
,则cos(∠1+∠2)的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com