
【题目】如图,△ABC中,∠ACB=90°,∠A=60°,点O为AB上一点,且3AO=AB,以OA为半径作半圆O,交AC于点D,AB于点E,DE与OC相交于F.
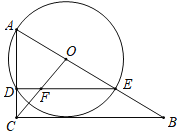
(1)求证:CB与⊙O相切;
(2)若AB=6,求DF的长度.
【答案】(1)见解析;(2)DF=![]() .
.
【解析】
(1)过O作OH⊥BC与H,根据直角三角形的性质得到OH=![]() OB,证得OH=OA,于是得到结论;
OB,证得OH=OA,于是得到结论;
(2)解直角三角形得到BC=![]() AB=3
AB=3![]() ,根据相似三角形的性质即可得到结论.
,根据相似三角形的性质即可得到结论.
(1)证明:过O作OH⊥BC与H,
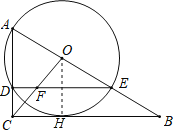
∵∠ACB=90°,
∴OH∥AC,
∵∠A=60°,
∴∠HOB=60°,
∴OH=![]() OB,
OB,
∵3AO=AB,
∴OA=![]() BO,
BO,
∴OH=OA,
∴CB与⊙O相切;
(2)解:∵AB=6,3AO=AB,
∴AE=4,OB=4,
∵△ABC中,∠ACB=90°,∠A=60°,
∴BC=![]() AB=3
AB=3![]() ,
,
∵AE是⊙O的直径,
∴∠ADE=90°,
∴DE∥BC,
∴△ADE∽△ACB,
△OEF∽△OBC,
∴![]() ,
,
∴![]() ,,
,,
∴![]() ,
,
∴DF=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】有这样一个问题:探究函数![]() 的图象和性质.小奥根据学习函数的经验,对函数
的图象和性质.小奥根据学习函数的经验,对函数![]() 的图象和性质进行了探究.下面是小奥的探究过程,请补充完整:
的图象和性质进行了探究.下面是小奥的探究过程,请补充完整:
(1)函数![]() 的自变量
的自变量![]() 的取值范围是_________;
的取值范围是_________;
(2)下表是![]() 与
与![]() 的几组对应值,则
的几组对应值,则![]() 的值为______,
的值为______,![]() 的值为______;
的值为______;
| … |
|
|
|
|
|
|
| 1 | 2 | 3 | 4 | 5 | … |
| … |
|
|
|
|
|
|
|
| 2 |
|
|
| … |
(3)如右图,在平面直角坐标系![]() 中,描出了以上表中各组对应值为坐标的点.根据描出的点,画出该函数的图象;
中,描出了以上表中各组对应值为坐标的点.根据描出的点,画出该函数的图象;
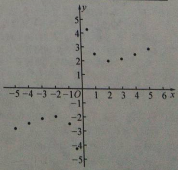
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是![]() .结合函数图象,写出该函数的其他两条性质:①_________,②_________.
.结合函数图象,写出该函数的其他两条性质:①_________,②_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣4,![]() ),B(﹣1,m)是一次函数y=kx+b与反比例函数y=
),B(﹣1,m)是一次函数y=kx+b与反比例函数y=![]() 图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D.
图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D.
(1)求m的值及一次函数解析式;
(2)P是线段AB上的一点,连接PC、PD,若△PCA和△PDB面积相等,求点P坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有![]() 名学生参加决赛,这
名学生参加决赛,这![]() 名学生同时默写
名学生同时默写![]() 首古诗词,若每正确默写出一首古诗词得
首古诗词,若每正确默写出一首古诗词得![]() 分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如下:
分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如下:
组别 | 成绩 | 频数(人数) |
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
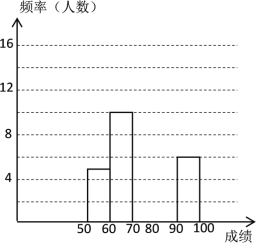
请结合图表完成下列各题: :
(1)①求表中![]() 的值;
的值;
②频数分布直方图补充完整;
(2)若测试成绩不低于![]() 分为优秀,则本次测试的优秀率是多少?
分为优秀,则本次测试的优秀率是多少?
(3)第![]() 组
组![]() 名同学中,有
名同学中,有![]() 名男同学,现将这
名男同学,现将这![]() 名同学平均分成两组进行对抗赛,且
名同学平均分成两组进行对抗赛,且![]() 名男同学每组分两人,求其中小华和小强两名男同学能分在同一组的概率.
名男同学每组分两人,求其中小华和小强两名男同学能分在同一组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰三角形纸片ABC中,AB=AC=10,BC=12,将此等腰三角形纸片沿底边BC上的高AD剪成两个全等的三角形,用这两个三角形拼成一个平行四边形,则所拼出的所有平行四边形中最长的对角线的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某景区的两个景点A、B处于同一水平地面上、一架无人机在空中沿MN方向水平飞行进行航拍作业,MN与AB在同一铅直平面内,当无人机飞行至C处时、测得景点A的俯角为45°,景点B的俯角为30°,此时C到地面的距离CD为100米,则两景点A、B间的距离为__米(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
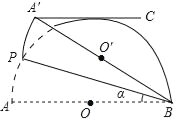
【题目】如图,AB是半圆O的直径,点P(不与点A,B重合)为半圆上一点,将图形沿BP折叠,分别得到点A,O的对应点点A′,O′,过点A′C∥AB,若A′C与半圆O恰好相切,则∠ABP的大小为_____°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com