
ЁОЬтФПЁПдкжБНЧзјБъЯЕжаЃЌЮвУЧВЛЗСНЋКсзјБъЃЌзнзјБъОљЮЊећЪ§ЕФЕуГЦжЎЮЊЁАжаЙњНсЁБЁЃ
ЃЈ1ЃЉЧѓКЏЪ§y=![]() x+2ЕФЭМЯёЩЯЫљгаЁАжаЙњНсЁБЕФзјБъЃЛ
x+2ЕФЭМЯёЩЯЫљгаЁАжаЙњНсЁБЕФзјБъЃЛ
ЃЈ2ЃЉЧѓКЏЪ§y=![]() ЃЈkЁй0ЃЌkЮЊГЃЪ§ЃЉЕФЭМЯёЩЯгаЧвжЛгаСНИіЁАжаЙњНсЁБЃЌЪдЧѓГіГЃЪ§kЕФжЕгыЯргІЁАжаЙњНсЁБЕФзјБъЃЛ
ЃЈkЁй0ЃЌkЮЊГЃЪ§ЃЉЕФЭМЯёЩЯгаЧвжЛгаСНИіЁАжаЙњНсЁБЃЌЪдЧѓГіГЃЪ§kЕФжЕгыЯргІЁАжаЙњНсЁБЕФзјБъЃЛ
ЃЈ3ЃЉШєЖўДЮКЏЪ§y=![]() ЃЈkЮЊГЃЪ§ЃЉЕФЭМЯёгыxжсЯрНЛЕУЕНСНИіВЛЭЌЕФЁАжаЙњНсЁБЃЌЪдЮЪИУКЏЪ§ЕФЭМЯёгыxжсЫљЮЇГЩЕФЦНУцЭМаЮжаЃЈКЌБпНчЃЉЃЌвЛЙВАќКЌгаЖрЩйИіЁАжаЙњНсЁБЃП
ЃЈkЮЊГЃЪ§ЃЉЕФЭМЯёгыxжсЯрНЛЕУЕНСНИіВЛЭЌЕФЁАжаЙњНсЁБЃЌЪдЮЪИУКЏЪ§ЕФЭМЯёгыxжсЫљЮЇГЩЕФЦНУцЭМаЮжаЃЈКЌБпНчЃЉЃЌвЛЙВАќКЌгаЖрЩйИіЁАжаЙњНсЁБЃП
ЁОД№АИЁПЃЈ1ЃЉЃЈ0,2ЃЉЃЛЃЈ2ЃЉЕБk=1ЪБЃЌЖдгІЁАжаЙњНсЁБЮЊЃЈ1,1ЃЉЃЈЃ1ЃЌЃ1ЃЉЃЛЕБk=Ѓ1ЪБЃЌЖдгІЁАжаЙњНсЁБЮЊЃЈ1ЃЌЃ1ЃЉЃЌЃЈЃ1,1ЃЉЃЛЃЈ3ЃЉ6Иі.
ЁОНтЮіЁП
ЪдЬтЃЈ1ЃЉвђЮЊxЪЧећЪ§ЃЌxЁй0ЪБЃЌ![]() xЪЧвЛИіЮоРэЪ§ЃЌЫљвдxЁй0ЪБЃЌ
xЪЧвЛИіЮоРэЪ§ЃЌЫљвдxЁй0ЪБЃЌ![]() x+2ВЛЪЧећЪ§ЃЌЫљвдx=0ЃЌy=2ЃЌОнДЫЧѓГіКЏЪ§y=
x+2ВЛЪЧећЪ§ЃЌЫљвдx=0ЃЌy=2ЃЌОнДЫЧѓГіКЏЪ§y=![]() x+2ЕФЭМЯѓЩЯЫљгаЁАжаЙњНсЁБЕФзјБъМДПЩЃЎ
x+2ЕФЭМЯѓЩЯЫљгаЁАжаЙњНсЁБЕФзјБъМДПЩЃЎ
ЃЈ2ЃЉЪзЯШХаЖЯГіЕБk=1ЪБЃЌКЏЪ§y=![]() ЃЈkЁй0ЃЌkЮЊГЃЪ§ЃЉЕФЭМЯѓЩЯгаЧвжЛгаСНИіЁАжаЙњНсЁБЃКЃЈ1ЃЌ1ЃЉЁЂЃЈЉ1ЁЂЉ1ЃЉЃЛШЛКѓХаЖЯГіЕБkЁй1ЪБЃЌКЏЪ§y=
ЃЈkЁй0ЃЌkЮЊГЃЪ§ЃЉЕФЭМЯѓЩЯгаЧвжЛгаСНИіЁАжаЙњНсЁБЃКЃЈ1ЃЌ1ЃЉЁЂЃЈЉ1ЁЂЉ1ЃЉЃЛШЛКѓХаЖЯГіЕБkЁй1ЪБЃЌКЏЪ§y=![]() ЃЈkЁй0ЃЌkЮЊГЃЪ§ЃЉЕФЭМЯѓЩЯзюЩйга4ИіЁАжаЙњНсЁБЃЌОнДЫЧѓГіГЃЪ§kЕФжЕгыЯргІЁАжаЙњНсЁБЕФзјБъМДПЩЃЎ
ЃЈkЁй0ЃЌkЮЊГЃЪ§ЃЉЕФЭМЯѓЩЯзюЩйга4ИіЁАжаЙњНсЁБЃЌОнДЫЧѓГіГЃЪ§kЕФжЕгыЯргІЁАжаЙњНсЁБЕФзјБъМДПЩЃЎ
ЃЈ3ЃЉЪзЯШСюЃЈk2Љ3k+2ЃЉx2+ЃЈ2k2Љ4k+1ЃЉx+k2Љk=0ЃЌдђ[ЃЈkЉ1ЃЉx+k][ЃЈkЉ2ЃЉx+ЃЈkЉ1ЃЉ]=0ЃЌЧѓГіx1ЁЂx2ЕФжЕЪЧЖрЩйЃЛШЛКѓИљОнx1ЁЂx2ЕФжЕЪЧећЪ§ЃЌЧѓГіkЕФжЕЪЧЖрЩйЃЛзюКѓИљОнКсзјБъЃЌзнзјБъОљЮЊећЪ§ЕФЕуГЦжЎЮЊЁАжаЙњНсЁБЃЌХаЖЯГіИУКЏЪ§ЕФЭМЯѓгыxжсЫљЮЇГЩЕФЦНУцЭМаЮжаЃЈКЌБпНчЃЉЃЌвЛЙВАќКЌгаЖрЩйИіЁАжаЙњНсЁБМДПЩЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЁпxЪЧећЪ§ЃЌxЁй0ЪБЃЌ![]() xЪЧвЛИіЮоРэЪ§ЃЌ
xЪЧвЛИіЮоРэЪ§ЃЌ
ЁрxЁй0ЪБЃЌ![]() x+2ВЛЪЧећЪ§ЃЌ
x+2ВЛЪЧећЪ§ЃЌ
Ёрx=0ЃЌy=2ЃЌ
МДКЏЪ§y=![]() x+2ЕФЭМЯѓЩЯЁАжаЙњНсЁБЕФзјБъЪЧЃЈ0ЃЌ2ЃЉЃЎ
x+2ЕФЭМЯѓЩЯЁАжаЙњНсЁБЕФзјБъЪЧЃЈ0ЃЌ2ЃЉЃЎ
ЃЈ2ЃЉЂйЕБk=1ЪБЃЌКЏЪ§y=![]() ЃЈkЁй0ЃЌkЮЊГЃЪ§ЃЉЕФЭМЯѓЩЯгаЧвжЛгаСНИіЁАжаЙњНсЁБЃК
ЃЈkЁй0ЃЌkЮЊГЃЪ§ЃЉЕФЭМЯѓЩЯгаЧвжЛгаСНИіЁАжаЙњНсЁБЃК
ЃЈ1ЃЌ1ЃЉЁЂЃЈЉ1ЁЂЉ1ЃЉЃЛ
ЂкЕБk=Љ1ЪБЃЌКЏЪ§y=![]() ЃЈkЁй0ЃЌkЮЊГЃЪ§ЃЉЕФЭМЯѓЩЯгаЧвжЛгаСНИіЁАжаЙњНсЁБЃК
ЃЈkЁй0ЃЌkЮЊГЃЪ§ЃЉЕФЭМЯѓЩЯгаЧвжЛгаСНИіЁАжаЙњНсЁБЃК
ЃЈ1ЃЌЉ1ЃЉЁЂЃЈЉ1ЃЌ1ЃЉЃЎ
ЂлЕБkЁйЁР1ЪБЃЌКЏЪ§y=![]() ЃЈkЁй0ЃЌkЮЊГЃЪ§ЃЉЕФЭМЯѓЩЯзюЩйга4ИіЁАжаЙњНсЁБЃК
ЃЈkЁй0ЃЌkЮЊГЃЪ§ЃЉЕФЭМЯѓЩЯзюЩйга4ИіЁАжаЙњНсЁБЃК
ЃЈ1ЃЌkЃЉЁЂЃЈЉ1ЃЌЉkЃЉЁЂЃЈkЃЌ1ЃЉЁЂЃЈЉkЃЌЉ1ЃЉЃЌетгыКЏЪ§y=![]() ЃЈkЁй0ЃЌkЮЊГЃЪ§ЃЉЕФЭМЯѓЩЯгаЧвжЛгаСНИіЁАжаЙњНсЁБУЌЖмЃЌ
ЃЈkЁй0ЃЌkЮЊГЃЪ§ЃЉЕФЭМЯѓЩЯгаЧвжЛгаСНИіЁАжаЙњНсЁБУЌЖмЃЌ
злЩЯПЩЕУЃЌk=1ЪБЃЌКЏЪ§y=![]() ЃЈkЁй0ЃЌkЮЊГЃЪ§ЃЉЕФЭМЯѓЩЯгаЧвжЛгаСНИіЁАжаЙњНсЁБЃКЃЈ1ЃЌ1ЃЉЁЂЃЈЉ1ЁЂЉ1ЃЉЃЛ
ЃЈkЁй0ЃЌkЮЊГЃЪ§ЃЉЕФЭМЯѓЩЯгаЧвжЛгаСНИіЁАжаЙњНсЁБЃКЃЈ1ЃЌ1ЃЉЁЂЃЈЉ1ЁЂЉ1ЃЉЃЛ
k=Љ1ЪБЃЌКЏЪ§y=![]() ЃЈkЁй0ЃЌkЮЊГЃЪ§ЃЉЕФЭМЯѓЩЯгаЧвжЛгаСНИіЁАжаЙњНсЁБЃКЃЈ1ЃЌЉ1ЃЉЁЂЃЈЉ1ЁЂ1ЃЉЃЎ
ЃЈkЁй0ЃЌkЮЊГЃЪ§ЃЉЕФЭМЯѓЩЯгаЧвжЛгаСНИіЁАжаЙњНсЁБЃКЃЈ1ЃЌЉ1ЃЉЁЂЃЈЉ1ЁЂ1ЃЉЃЎ
ЃЈ3ЃЉСюЃЈk2Љ3k+2ЃЉx2+ЃЈ2k2Љ4k+1ЃЉx+k2Љk=0ЃЌ
дђ[ЃЈkЉ1ЃЉx+k][ЃЈkЉ2ЃЉx+ЃЈkЉ1ЃЉ]=0ЃЌ
Ёр
Ёр![]() ЃЌ
ЃЌ
ећРэЃЌПЩЕУ
x1x2+2x2+1=0ЃЌ
Ёрx2ЃЈx1+2ЃЉ=Љ1ЃЌ
Ёпx1ЁЂx2ЖМЪЧећЪ§ЃЌ
Ёр![]() Лђ
Лђ![]()
Ёр![]() Лђ
Лђ![]()
ЂйЕБ![]() ЪБЃЌ
ЪБЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёрk=![]() ЃЛ
ЃЛ
ЂкЕБ![]() ЪБЃЌ
ЪБЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёрk=kЉ1ЃЌЮоНтЃЛ
злЩЯЃЌПЩЕУ
k=![]() ЃЌx1=Љ3ЃЌx2=1ЃЌ
ЃЌx1=Љ3ЃЌx2=1ЃЌ
y=ЃЈk2Љ3k+2ЃЉx2+ЃЈ2k2Љ4k+1ЃЉx+k2Љk
=[(![]() )2Љ3ЁС
)2Љ3ЁС![]() +2]x2+[2ЁСЃЈ
+2]x2+[2ЁСЃЈ![]() ЃЉ2Љ4ЁС
ЃЉ2Љ4ЁС![]() +1]x+ЃЈ
+1]x+ЃЈ![]() ЃЉ2Љ
ЃЉ2Љ![]()
=Љ![]() x2Љ
x2Љ![]() x+
x+![]()
ЂйЕБx=Љ2ЪБЃЌ
y=Љ![]() x2Љ
x2Љ![]() x+
x+![]() =Љ
=Љ![]() ЁСЃЈЉ2ЃЉ2Љ
ЁСЃЈЉ2ЃЉ2Љ![]() ЁСЃЈЉ2ЃЉ+
ЁСЃЈЉ2ЃЉ+![]()
=![]()
ЂкЕБx=Љ1ЪБЃЌ
y=Љ![]() x2Љ
x2Љ![]() x+
x+![]()
=Љ![]() ЁСЃЈЉ1ЃЉ2Љ
ЁСЃЈЉ1ЃЉ2Љ![]() ЁСЃЈЉ1ЃЉ+
ЁСЃЈЉ1ЃЉ+![]()
=1
ЂлЕБx=0ЪБЃЌy=![]() ЃЌ
ЃЌ
СэЭтЃЌИУКЏЪ§ЕФЭМЯѓгыxжсЫљЮЇГЩЕФЦНУцЭМаЮжаxжсЩЯЕФЁАжаЙњНсЁБга3ИіЃК
ЃЈЉ2ЃЌ0ЃЉЁЂЃЈЉ1ЁЂ0ЃЉЁЂЃЈ0ЃЌ0ЃЉЃЎ
злЩЯЃЌПЩЕУ
ШєЖўДЮКЏЪ§y=ЃЈk2Љ3k+2ЃЉx2+ЃЈ2k2Љ4k+1ЃЉx+k2ЉkЃЈkЮЊГЃЪ§ЃЉЕФЭМЯѓгыxжсЯрНЛЕУЕНСНИіВЛЭЌЕФЁАжаЙњНсЁБЃЌ
ИУКЏЪ§ЕФЭМЯѓгыxжсЫљЮЇГЩЕФЦНУцЭМаЮжаЃЈКЌБпНчЃЉЃЌвЛЙВАќКЌга6ИіЁАжаЙњНсЁБЃКЃЈЉ3ЃЌ0ЃЉЁЂЃЈЉ2ЃЌ0ЃЉЁЂЃЈЉ1ЃЌ0ЃЉЃЈЉ1ЃЌ1ЃЉЁЂЃЈ0ЃЌ0ЃЉЁЂЃЈ1ЃЌ0ЃЉЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
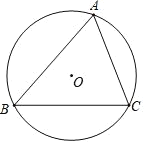
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌABЃНBCЃЌвдABЮЊжБОЖЕФЁбOНЛBCгкЕуDЃЌНЛACгкЕуFЃЌЙ§ЕуCзїCEЁЮABЃЌгыЙ§ЕуAЕФЧаЯпЯрНЛгкЕуEЃЌСЌНгADЃЎ
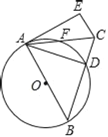
ЃЈ1ЃЉЧѓжЄЃКADЃНAEЃЎ
ЃЈ2ЃЉШєABЃН10ЃЌsinЁЯDACЃН![]() ЧѓADЕФГЄЃЎ
ЧѓADЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌХзЮяЯпyЃНax2Љ![]() x+cНЛxжсгкAЃЌBСНЕуЃЌНЛyжсгкЕуCЃЎжБЯпyЃНЉ
x+cНЛxжсгкAЃЌBСНЕуЃЌНЛyжсгкЕуCЃЎжБЯпyЃНЉ![]() x+3ОЙ§ЕуBЃЌCЃЎ
x+3ОЙ§ЕуBЃЌCЃЎ
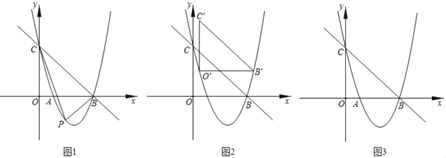
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєЕуPЮЊжБЯпBCЯТЗНЕФХзЮяЯпЩЯвЛЖЏЕуЃЈВЛгыЕуBЃЌCжиКЯЃЉЃЌдђЁїPBCЕФУцЛ§ФмЙЛЕШгкЁїBOCЕФУцЛ§Т№ЃПШєФмЃЌЧѓГіЯргІЕФЕуPЕФзјБъЃЛШєВЛФмЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЯжАбЁїBOCЦНвЦжСШчЭМЫљЪОЕФЮЛжУЃЌДЫЪБШ§НЧаЮЫЎЦНЗНЯђвЛБпЕФСНИіЖЫЕуЕуOЁфгыЕуBЁфЖМдкХзЮяЯпЩЯЃЌГЦЕуOЁфКЭЕуBЁфЮЊЁїBOCдкХзЮяЯпЩЯЕФвЛЁАПЈЕуЖдЁБЃЛШчЙћАбЁїBOCа§зЊвЛЖЈНЧЖШЃЌЪЙЕУЦфгрБпЮЛгкЫЎЦНЗНЯђШЛКѓЦНвЦЃЌФмЙЛЕУЕНетИіШ§НЧаЮдкХзЮяЯпЩЯаТЕФЁАПЈЕуЖдЁБЃЎЧыжБНгаДГіЁїBOCдквбжЊХзЮяЯпЩЯЫљгаЁАПЈЕуЖдЁБЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхЃКвЛзщСкБпЯрЕШЧвЖдНЧЛЅВЙЕФЫФБпаЮНазіЁАСкЕШЖдВЙЫФБпаЮЁБ
ШчЭМ1ЃЌЫФБпаЮABCDжаЃЌABЃНBCЃЌЁЯB+ЁЯDЃН180ЁуЃЈЛђЁЯA+ЁЯCЃН180ЁуЃЉЃЌдђЫФБпаЮABCDНазіЁАСкЕШЖдВЙЫФБпаЮЁБЃЎ
ИХФюРэНт
ЃЈ1ЃЉдквдЯТЫФжжЭМаЮжаЃКЂйЦНааЫФБпаЮЃЌЂкСтаЮЃЌЂлОиаЮЃЌЂме§ЗНаЮЃЛвЛЖЈЪЧЁАСкЕШЖдВЙЫФБпаЮЁБЕФЪЧЁЁ ЁЁЃЛЃЈЬюаДађКХЃЉ
ЃЈ2ЃЉШчЭМ2ЃЌЕуAЁЂBЁЂCЪЧЭјИёжаИёЕуЃЌЧыевГіСНИіИёЕуP1ЃЌP2ЃЌСЌНгP1AЁЂP1CЃЌP2AЁЂP2CЛГіЫФБпаЮP1ABCЃЌP2ABCЃЌЪЙЫФБпаЮP1ABCЃЌP2ABCОљЮЊЁАСкЕШЖдВЙЫФБпаЮЁБЃЎ
аджЪжЄУї
ЃЈ3ЃЉШчЭМ1ЃЌЫФБпаЮABCDжаЃЌABЃНBCЃЌЁЯA+ЁЯCЃН180ЁуЃЌСЌНгBDЃЌЧѓжЄЃКBDЦНЗжЁЯADCЃЎ
жЊЪЖдЫгУ
ЃЈ4ЃЉШчЭМ3ЃЌдкЁАСкЕШЖдВЙЫФБпаЮЁБABCDжаЃЌТњзуABЃНADЃЌAB+BCЃН6ЃЌЁЯADCЃН60ЁуЪБЃЌШє2ЁмBCЃМ3ЃЌЧѓЫФБпаЮABCDЕФУцЛ§ЕФзюДѓжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНax2+bx+4НЛyжсгкЕуAЃЌВЂОЙ§BЃЈ4ЃЌ4ЃЉКЭCЃЈ6ЃЌ0ЃЉСНЕуЃЌЕуDЕФзјБъЮЊЃЈ4ЃЌ0ЃЉЃЌСЌНгADЃЌBCЃЌЕуFДгЕуOГіЗЂЃЌвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШбиЯпЖЮOCЗНЯђдЫЖЏЃЌЕНДяЕуCКѓЭЃжЙдЫЖЏЃКЕуMЭЌЪБДгЕуDГіЗЂвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШбиxжсе§ЗНЯђдЫЖЏЃЌЕБЕуFЭЃжЙЪБЕуMвВЭЃжЙдЫЖЏЃЎЩшЕуFЕФдЫЖЏЪБМфЮЊtУыЃЌЙ§ЕуFзїABЕФДЙЯпEFНЛжБЯпABгкЕуEЃЌНЛADгкЕуHЃЎ

ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉвдЯпЖЮEHЮЊаББпЯђгвзїЕШбќжБНЧЁїEHGЃЌЕБЕуGТфдкЕквЛЯѓЯоФкЕФХзЮяЯпЩЯЪБЃЌЧѓГіtЕФжЕЃЛ
ЃЈ3ЃЉЩшЁїEFMгыЫФБпаЮADCBжиКЯЪБЕФУцЛ§ЮЊSЃЌЧыжБНгаДГіSгыtЕФКЏЪ§ЙиЯЕЪНгыЯргІЕФздБфСПtЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌМзЁЂввСНДЌЭЌЪБгЩИлПкAГіЗЂПЊЭљКЃЕКBЃЌМзДЌбиЖЋББЗНЯђЯђКЃЕКBКНааЃЌЦфЫйЖШЮЊ15КЃРя/аЁЪБЃЛввДЌЫйЖШЮЊ20КЃРя/аЁЪБЃЌЯШбие§ЖЋЗНЯђКНаа1аЁЪБКѓЃЌЕНДяCИлПкНгТУПЭЃЌЭЃСєАыаЁЪБКѓдйзЊЯђББЦЋЖЋ30ЁуЗНЯђПЊЭљBЕКЃЌЦфЫйЖШШдЮЊ20КЃРя/аЁЪБЃЎ
ЃЈ1ЃЉЧѓИлПкAЕНКЃЕКBЕФОрРыЃЛ
ЃЈ2ЃЉBЕКНЈгавЛзљЕЦЫўЃЌдкРыЕЦЫўЗНдВ5КЃРяФкЖМПЩвдПДМћЕЦЫўЃЌЮЪМзЁЂввСНДЌФФвЛЫвЯШПДЕНЕЦЫўЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНЉx2+bx+cЙ§ЕШбќRtЁїOABЕФAЃЌBСНЕуЃЌЕуBдкЕуAЕФгвВрЃЌжБНЧЖЅЕуAЃЈ0ЃЌ3ЃЉЃЎ
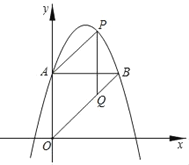
ЃЈ1ЃЉЧѓbЃЌcЕФжЕЃЎ
ЃЈ2ЃЉPЪЧABЩЯЗНХзЮяЯпЩЯЕФвЛЕуЃЌзїPQЁЭABНЛOBгкЕуQЃЌСЌНгAPЃЌЪЧЗёДцдкЕуPЃЌЪЙЫФБпаЮAPQOЪЧЦНааЫФБпаЮЃПШєДцдкЃЌЧыЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЪ§бЇПЮЩЯЃЌРЯЪІЬсГіРћгУГпЙцзїЭМЭъГЩЯТУцЮЪЬтЃКвбжЊЃКЁїABCЪЧЁбOЕФФкНгШ§НЧаЮЃЎЧѓзїЃКЁїABCжаЁЯBACЕФЦНЗжЯпЃЎ
аЁУїЕФзїЗЈШчЯТЃК
ЃЈ1ЃЉзїBCБпЕФДЙжБЦНЗжЯпDEЃЌНЛBCгкЕуDЃЌНЛЛЁBCгкЕуEЃЛ
ЃЈ2ЃЉСЌНгAEЃЌНЛBCБпгкЕуFЃЛдђЯпЖЮAFЮЊЫљЧѓЁїABCжаЁЯBACЕФЦНЗжЯпЃЎИљОнаЁУїЩшМЦЕФГпЙцзїЭМЙ§ГЬЃЌ
ЂйдкЭМжаВЙШЋЭМаЮЃЈГпЙцзїЭМЃЌБЃСєзїЭМКлМЃЃЉЃЛ
ЂкЭъГЩЯТУцЕФжЄУїЃЎ
жЄУїЃКЁпOBЃНOCЃЌDEЪЧЯпЖЮBCЕФДЙжБЦНЗжЯп
ЁрдВаФOдкжБЯпDEЩЯЃЈЁЁ ЁЁЃЉЃЎ
ЁпDEЁЭBCЃЌ
Ёр![]() ЃЈЁЁ ЁЁЃЉЃЎ
ЃЈЁЁ ЁЁЃЉЃЎ
ЁрЁЯBAEЃНЁЯCAEЃЈЁЁ ЁЁЃЉЃЌ
ЁрЯпЖЮAFЮЊЫљЧѓЁїABCжаЁЯBACЕФЦНЗжЯпЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
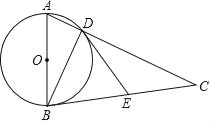
ЁОЬтФПЁПШчЭМЃЌдкШёНЧЁїABCжаЃЌвдABЮЊжБОЖЕФЁбOНЛACгкЕуDЃЌЙ§ЕуDзїЁбOЕФЧаЯпDEНЛБпBCгкЕуEЃЌСЌНсBDЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁЯABDЃНЁЯCDEЃЎ
ЃЈ2ЃЉШєACЃН28ЃЌtanAЃН2ЃЌADЃКDCЃН1ЃК3ЃЌЧѓDEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com