
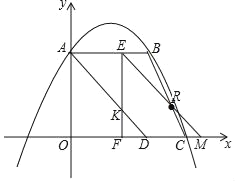
【题目】如图,抛物线y=ax2+bx+4交y轴于点A,并经过B(4,4)和C(6,0)两点,点D的坐标为(4,0),连接AD,BC,点F从点O出发,以每秒1个单位长度的速度沿线段OC方向运动,到达点C后停止运动:点M同时从点D出发以每秒1个单位长度的速度沿x轴正方向运动,当点F停止时点M也停止运动.设点F的运动时间为t秒,过点F作AB的垂线EF交直线AB于点E,交AD于点H.

(1)求抛物线的解析式;
(2)以线段EH为斜边向右作等腰直角△EHG,当点G落在第一象限内的抛物线上时,求出t的值;
(3)设△EFM与四边形ADCB重合时的面积为S,请直接写出S与t的函数关系式与相应的自变量t的取值范围.
【答案】(1)y=﹣![]() x2+
x2+![]() x+4;(2)t=
x+4;(2)t=![]() ;(3)S=
;(3)S=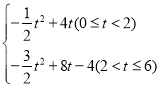 .
.
【解析】
(1)由题意得:函数的对称轴为:x=2,则函数与x轴的另外一个交点坐标为(2,0),则函数的表达式为:y=a(x+2)(x6)=a(x24x12),即可求解;
(2)求出点G(![]() ,
,![]() ),将点G的坐标代入表达式,即可求解;
),将点G的坐标代入表达式,即可求解;
(3)分0<t≤2、2<t≤6两种情况分别求解即可.
(1)由题意得:函数的对称轴为:x=2,则函数与x轴的另外一个交点坐标为(﹣2,0),
则函数的表达式为:y=a(x+2)(x﹣6)=a(x2﹣4x﹣12),
则﹣12a=4,解得:a=﹣![]() ,
,
故抛物线的表达式为:y=﹣![]() x2+
x2+![]() x+4;
x+4;
(2)将点A、D的坐标代入一次函数表达式并解得:
直线AD的表达式为:y=﹣x+4,
则点E、F的坐标分别为:(t,4)、(t,0),
则点H(t,4﹣t),则点G(![]() ,4﹣
,4﹣![]() t),
t),
将点G的坐标代入表达式得:4﹣![]() t=﹣
t=﹣![]() ·(
·(![]() )2+
)2+![]() ·
·![]() +4,
+4,
解得:t=![]() ;
;
(3)点M(t+4,0),点E(t,4)、点F(t,0),
①当0<t≤2时,设EF交AD于点

S=S△EFM﹣S△FND=8﹣![]() ×(4﹣t)2=﹣
×(4﹣t)2=﹣![]() t2+4t,
t2+4t,
②2<t≤6时,
设直线EM交BC于点R,EF交AD于点K(t,4﹣t),
同理可得:直线ME的表达式为:y=﹣x+t+4,
直线BC的表达式为:y=﹣2x+12,
联立上述两式并解得:x=8﹣t,
故点R(8﹣t,2t﹣4),
S=S△EFM﹣S△RCM﹣S△KFD=![]() 4×4﹣
4×4﹣![]() (t+4﹣6)(2t﹣4)﹣
(t+4﹣6)(2t﹣4)﹣![]() ×(4﹣t)2=﹣
×(4﹣t)2=﹣![]() t2+8t﹣4;
t2+8t﹣4;
故S=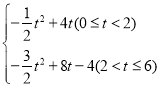 .
.


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
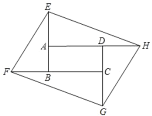
【题目】如图,将矩形ABCD的四边BA,CB,DC,AD分别延长至点EF,G,H,使得AE=BF=CG=DH.已知AB=1,BC=2,∠BEF=30°,则tan∠AEH的值为( )
A.2B.![]() C.
C.![]() ﹣1D.
﹣1D.![]() +1
+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 图象的一部分如图所示,给出以下结论:
图象的一部分如图所示,给出以下结论:![]() ;
;![]() 当
当![]() 时,函数有最大值;
时,函数有最大值;![]() 方程
方程![]() 的解是
的解是![]() ,
,![]() ;
;![]() ,其中结论错误的个数是
,其中结论错误的个数是![]()
![]()
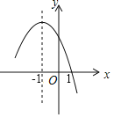
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市正在开展“食品安全城市”创建活动,为了解学生对食品安全知识的了解情况,学校从2019年1月﹣5月等月随机抽取了部分学生进行问卷调查(被调查学生每人只能选一项),将调查站果按照“A非常了解、B了解、C了解较少、D不了解”四类情况分别选行统计,并绘制成图1、图2两幅统计图、根据统计图提供的信息解答下列问题:
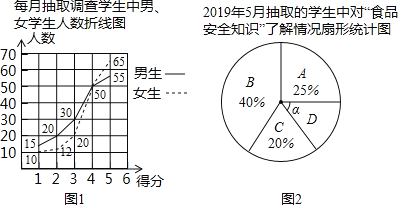
(1) 月抽取的调查人数最少: 月抽取的调查人数中男生、女生人数相等;
(2)求图2中“D不了解”在扇形图中所占的圆心角α的度数:
(3)若该校2019年5月份在校学生3600名,请你估计对食品安全知识“A非常了解和B了解”的学生总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
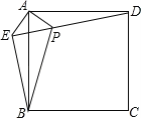
【题目】如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=![]() .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为![]() ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+![]() ;⑤S正方形ABCD=4+
;⑤S正方形ABCD=4+![]() .其中正确结论的序号是 .
.其中正确结论的序号是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,我们不妨将横坐标,纵坐标均为整数的点称之为“中国结”。
(1)求函数y=![]() x+2的图像上所有“中国结”的坐标;
x+2的图像上所有“中国结”的坐标;
(2)求函数y=![]() (k≠0,k为常数)的图像上有且只有两个“中国结”,试求出常数k的值与相应“中国结”的坐标;
(k≠0,k为常数)的图像上有且只有两个“中国结”,试求出常数k的值与相应“中国结”的坐标;
(3)若二次函数y=![]() (k为常数)的图像与x轴相交得到两个不同的“中国结”,试问该函数的图像与x轴所围成的平面图形中(含边界),一共包含有多少个“中国结”?
(k为常数)的图像与x轴相交得到两个不同的“中国结”,试问该函数的图像与x轴所围成的平面图形中(含边界),一共包含有多少个“中国结”?
查看答案和解析>>
科目:初中数学 来源: 题型:
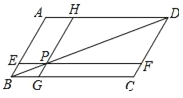
【题目】如图,在ABCD中,过对角线BD上一点P作EF∥BC,GH∥AB,且CG=2BG,S△BPG=1,则SAEPH=( )
A. 3B. 4C. 5D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,抛物线
两点,抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴另一交点为
轴另一交点为![]() ,顶点为
,顶点为![]() .
.
(1)求抛物线的解析式;
(2)在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的值最小,求
的值最小,求![]() 的最小值;
的最小值;
(3)在抛物线的对称轴上是否存在一点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若a=4,b=5,则该矩形的面积为( )
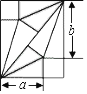
A.50B.40C.30D.20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com