
【题目】如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=![]() .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为![]() ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+![]() ;⑤S正方形ABCD=4+
;⑤S正方形ABCD=4+![]() .其中正确结论的序号是 .
.其中正确结论的序号是 .
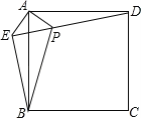
【答案】①③⑤
【解析】
①利用同角的余角相等,易得∠EAB=∠PAD,再结合已知条件利用SAS可证两三角形全等;
②过B作BF⊥AE,交AE的延长线于F,利用③中的∠BEP=90°,利用勾股定理可求BE,结合△AEP是等腰直角三角形,可证△BEF是等腰直角三角形,再利用勾股定理可求EF、BF;
③利用①中的全等,可得∠APD=∠AEB,结合三角形的外角的性质,易得∠BEP=90°,即可证;
④连接BD,求出△ABD的面积,然后减去△BDP的面积即可;
⑤在Rt△ABF中,利用勾股定理可求AB2,即是正方形的面积.
①∵∠EAB+∠BAP=90°,∠PAD+∠BAP=90°,
∴∠EAB=∠PAD,
又∵AE=AP,AB=AD,
∵在△APD和△AEB中,
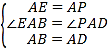 ,
,
∴△APD≌△AEB(SAS);
故此选项成立;
③∵△APD≌△AEB,
∴∠APD=∠AEB,
∵∠AEB=∠AEP+∠BEP,∠APD=∠AEP+∠PAE,
∴∠BEP=∠PAE=90°,
∴EB⊥ED;
故此选项成立;
②过B作BF⊥AE,交AE的延长线于F,
∵AE=AP,∠EAP=90°,
∴∠AEP=∠APE=45°,
又∵③中EB⊥ED,BF⊥AF,
∴∠FEB=∠FBE=45°,
又∵BE=![]() =
=![]() =
=![]() ,
,
∴BF=EF=![]() ,
,
故此选项不正确;
④如图,连接BD,在Rt△AEP中,
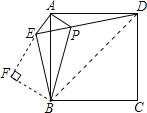
∵AE=AP=1,
∴EP=![]() ,
,
又∵PB=![]() ,
,
∴BE=![]() ,
,
∵△APD≌△AEB,
∴PD=BE=![]() ,
,
∴S△ABP+S△ADP=S△ABD-S△BDP=![]() S正方形ABCD-
S正方形ABCD-![]() ×DP×E=
×DP×E=![]() ×(4+
×(4+![]() )-
)-![]() ×
×![]() ×
×![]() =
=![]() +
+![]() .
.
故此选项不正确.
⑤∵EF=BF=![]() ,AE=1,
,AE=1,
∴在Rt△ABF中,AB2=(AE+EF)2+BF2=4+![]() ,
,
∴S正方形ABCD=AB2=4+![]() ,
,
故此选项正确.
故答案为:①③⑤.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
【题目】某演唱会购买门票的方式有两种
方式一:若单位赞助广告费10万元,则该单位所购门票的价格为每张0.02万元;(注方式一中总费用=广告费用+门票费用)
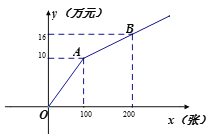
方式二:按如图所示的购买门票方式.
设购买门票x张,总费用为y万元.
(1)求按方式一购买时y与x的函数关系式
(2)若甲、乙两个单位分采用方式一,方式二购买本场演唱会门共400张,且乙单位购买超过100张,两单位共花费27.2万元,求甲、乙两单位各购买门票多少张?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形是平行四边形,以AB为直径的![]() 经过点D, E是
经过点D, E是![]() 上一点,且
上一点,且![]() .
.
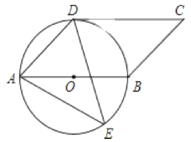
(1)判断CD与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2) 若BC=2 .求阴影部分的面积.(结果保留π 的形式).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国科学技术馆有“圆与非圆”展品,涉及了“等宽曲线”的知识.因为圆的任何一对平行切线的距离总是相等的,所以圆是“等宽曲线”.除了例以外,还有一些几何图形也是“等宽曲线”,如勒洛只角形(图1),它是分别以等边三角形的征个顶点为圆心,以边长为半径,在另两个顶点间画一段圆弧.三段圆弧围成的曲边三角形.图2是等宽的勒洛三角形和圆.
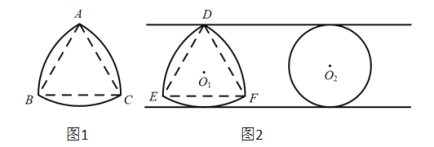
下列说法中错误的是( )
A.勒洛三角形是轴对称图形
B.图1中,点A到![]() 上任意一点的距离都相等
上任意一点的距离都相等
C.图2中,勒洛三角形上任意一点到等边三角形DEF的中心![]() 的距离都相等
的距离都相等
D.图2中,勒洛三角形的周长与圆的周长相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的两边AD、AB的长分别为3、8,边BC落在x轴上,E是DC的中点,连接AE.
(1)若点B坐标为(﹣6,0),求直线AE的表达式;
(2)反比例函数y=![]() (x<0)的图象经过点E,与AB交于点F,若AF﹣AE=2,求反比例函数的表达式;
(x<0)的图象经过点E,与AB交于点F,若AF﹣AE=2,求反比例函数的表达式;
(3)在(2)的条件下,连接矩形ABCD两对边AD与BC的中点M、N,设线段MN与反比例函数图象交于点P,将线段MN沿x轴向右平移n个单位,若MP<NP,直接写出n的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+4交y轴于点A,并经过B(4,4)和C(6,0)两点,点D的坐标为(4,0),连接AD,BC,点F从点O出发,以每秒1个单位长度的速度沿线段OC方向运动,到达点C后停止运动:点M同时从点D出发以每秒1个单位长度的速度沿x轴正方向运动,当点F停止时点M也停止运动.设点F的运动时间为t秒,过点F作AB的垂线EF交直线AB于点E,交AD于点H.

(1)求抛物线的解析式;
(2)以线段EH为斜边向右作等腰直角△EHG,当点G落在第一象限内的抛物线上时,求出t的值;
(3)设△EFM与四边形ADCB重合时的面积为S,请直接写出S与t的函数关系式与相应的自变量t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011山东济南,27,9分)如图,矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线![]() 经过A、C两点,与AB边交于点D.
经过A、C两点,与AB边交于点D.
(1)求抛物线的函数表达式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式,并求出m为何值时,S取得最大值;
②当S最大时,在抛物线![]() 的对称轴l上若存在点F,使△FDQ为直角三角形,请直接写出所有符合条件的F的坐标;若不存在,请说明理由.
的对称轴l上若存在点F,使△FDQ为直角三角形,请直接写出所有符合条件的F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E是BC上的一点,F在线段DE上,且∠AFE=∠ADC.
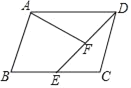
(1)若∠AFE=70°,∠DEC=40°,求∠DAF的大小;
(2)若DE=AD,求证:△AFD≌△DCE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某庄有甲、乙两家草莓采摘园的草莓销售价格相同,春节期间,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为![]() (千克),在甲园所需总费用为
(千克),在甲园所需总费用为![]() (元),在乙园所需总费用为
(元),在乙园所需总费用为![]() (元),
(元),![]() 、
、![]() 与
与![]() 之间的函数关系如图所示.
之间的函数关系如图所示.

(1)甲采摘园的门票是_____元,两个采摘园优惠前的草莓单价是每千克____元;
(2)当![]() 时,求
时,求![]() 与
与![]() 的函数表达式;
的函数表达式;
(3)游客在“春节期间”采摘多少千克草莓时,甲、乙两家采摘园的总费用相同.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com