
【题目】如图,矩形ABCD的两边AD、AB的长分别为3、8,边BC落在x轴上,E是DC的中点,连接AE.
(1)若点B坐标为(﹣6,0),求直线AE的表达式;
(2)反比例函数y=![]() (x<0)的图象经过点E,与AB交于点F,若AF﹣AE=2,求反比例函数的表达式;
(x<0)的图象经过点E,与AB交于点F,若AF﹣AE=2,求反比例函数的表达式;
(3)在(2)的条件下,连接矩形ABCD两对边AD与BC的中点M、N,设线段MN与反比例函数图象交于点P,将线段MN沿x轴向右平移n个单位,若MP<NP,直接写出n的取值范围.

【答案】(1)y=﹣![]() x;(2)y=﹣
x;(2)y=﹣![]() ;(3)
;(3)![]() <n≤2.
<n≤2.
【解析】
(1)由矩形的性质结合点B的坐标,可得出点A,E的坐标,再利用待定系数法即可求出直线AE的表达式;(2)由DC的长结合反比例函数图象上点的坐标特征,可得出点E的坐标为(![]() ,4),在Rt△ADE中,利用勾股定理可求出AE的长,结合AF﹣AE=2可得出AF的长,由BC=3可得出点F的坐标为(
,4),在Rt△ADE中,利用勾股定理可求出AE的长,结合AF﹣AE=2可得出AF的长,由BC=3可得出点F的坐标为(![]() ﹣3,1),再利用反比例函数图象上点的坐标特征,可得出关于m的一元一次方程,解之即可得出m的值,进而可得出反比例函数的表达式;(3)由(2)可得出点M,N的坐标,结合平移的性质可得出平移后点M,N的坐标,设设点P的坐标为(﹣
﹣3,1),再利用反比例函数图象上点的坐标特征,可得出关于m的一元一次方程,解之即可得出m的值,进而可得出反比例函数的表达式;(3)由(2)可得出点M,N的坐标,结合平移的性质可得出平移后点M,N的坐标,设设点P的坐标为(﹣![]() +n,y),由点P在MN上且MP<NP,可得出y的取值范围,利用反比例函数图象上点的坐标特征,可得出关于n的一元一次不等式组,解之即可得出n的取值范围.
+n,y),由点P在MN上且MP<NP,可得出y的取值范围,利用反比例函数图象上点的坐标特征,可得出关于n的一元一次不等式组,解之即可得出n的取值范围.
(1)由题意,可知:点A的坐标为(﹣6,8),点E的坐标为(﹣3,4).
设直线AE的表达式为y=kx+b(k≠0),
将A(﹣6,8),E(﹣3,4)代入y=kx+b,得: ![]() ,
,
解得: ,
,
∴当点B的坐标为(﹣6,0)时,直线AE的表达式为y=﹣![]() x.
x.
(2)∵反比例函数y=![]() 的图象经过点E,E是DC的中点,DC=8,
的图象经过点E,E是DC的中点,DC=8,
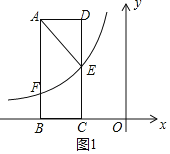
∴点E的坐标为(![]() ,4).
,4).
在Rt△ADE中,AD=3,DE=4,∠ADE=90°,
∴AE=![]() =5.
=5.
∵AF﹣AE=2,
∴AF=7,
∴BF=AB﹣AF=1,
∴点F的坐标为(![]() ﹣3,1).
﹣3,1).
∵点F在反比例函数y=![]() 的图象上,
的图象上,
∴![]() ﹣3=m,
﹣3=m,
解得:m=﹣4,
∴反比例函数的表达式为y=﹣![]() .
.
(3)由(2)可知:点B的坐标为(﹣4,0),点C的坐标为(﹣1,0),
∴点M的坐标为(﹣![]() ,8),点N的坐标为(﹣
,8),点N的坐标为(﹣![]() ,0),
,0),
∴平移后的点M的坐标为(﹣![]() +n,8),平移后点N的坐标为(﹣
+n,8),平移后点N的坐标为(﹣![]() +n,0).
+n,0).

设点P的坐标为(﹣![]() +n,y),∵点P在MN上,且MP<NP,
+n,y),∵点P在MN上,且MP<NP,
∴4<y≤8.
∵点P在反比例函数y=﹣![]() 的图象上,
的图象上,
∴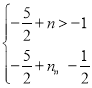 ,
,
解得:![]() <n≤2.
<n≤2.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
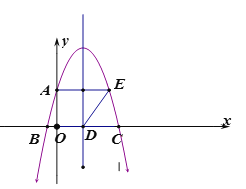
【题目】已知:如图抛物线y=ax2+bx+![]() 与y轴交于点A,与x轴交于点B、点C.连接AB,以AB为边向右作平行四边形ABDE,点E落在抛物线上,点D落在x轴上,若抛物线的对称轴恰好经过点D,且∠ABD=60°,则这条抛物线的解析式为( )
与y轴交于点A,与x轴交于点B、点C.连接AB,以AB为边向右作平行四边形ABDE,点E落在抛物线上,点D落在x轴上,若抛物线的对称轴恰好经过点D,且∠ABD=60°,则这条抛物线的解析式为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
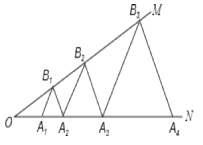
【题目】如图,已知:∠MON=30°,点A![]() 、A
、A![]() 、A
、A![]() …在射线ON上,点B
…在射线ON上,点B![]() 、B
、B![]() 、B
、B![]() …在射线OM上,△A
…在射线OM上,△A![]() B
B![]() A
A![]() 、△A
、△A![]() B
B![]() A
A![]() 、△A
、△A![]() B
B![]() A
A![]() …均为等边三角形,若OA
…均为等边三角形,若OA![]() =1,则△A
=1,则△A![]() B
B![]() A
A![]() 的边长为____
的边长为____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一棵大树在一次强台风中折断倒下,未折断树杆![]() 与地面仍保持垂直的关系,而折断部分
与地面仍保持垂直的关系,而折断部分![]() 与未折断树杆
与未折断树杆![]() 形成
形成![]() 的夹角.树杆
的夹角.树杆![]() 旁有一座与地面垂直的铁塔
旁有一座与地面垂直的铁塔![]() ,测得
,测得![]() 米,塔高
米,塔高![]() 米.在某一时刻的太阳照射下,未折断树杆
米.在某一时刻的太阳照射下,未折断树杆![]() 落在地面的影子
落在地面的影子![]() 长为
长为![]() 米,且点
米,且点![]() 、
、![]() 、
、![]() 、
、![]() 在同一条直线上,点
在同一条直线上,点![]() 、
、![]() 、
、![]() 也在同一条直线上.求这棵大树没有折断前的高度.(结果精确到
也在同一条直线上.求这棵大树没有折断前的高度.(结果精确到![]() ,参考数据:
,参考数据: ![]() ,
, ![]() ,
, ![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市开展早市促销活动,为早到的顾客准备一份简易早餐,餐品有四样:A.韭菜包,B.豆沙包,C.鸡蛋,D.油条.超市约定:“随机发放,早餐一人一份,一份两样,一样一个.”
(1)按约定,某顾客该天“早餐得到两个鸡蛋”是 事件(填“随机”“必然”或“不可能”):
(2)请用列表或画树状图的方法,求出某顾客该天“早餐刚好得到一个韭菜包和一根油条”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
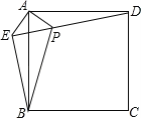
【题目】如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=![]() .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为![]() ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+![]() ;⑤S正方形ABCD=4+
;⑤S正方形ABCD=4+![]() .其中正确结论的序号是 .
.其中正确结论的序号是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列图形:

它们是按一定规律排列的,依照此规律,第5个图形中的五角星的个数为___,第n个图形中的五角星(n为正整数)个数为____(用含n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)尺规作图:如图,![]() 、
、![]() 是平面上两个定点,在平面上找一点
是平面上两个定点,在平面上找一点![]() ,使
,使![]() 构成等腰直角三角形,且
构成等腰直角三角形,且![]() 为直角顶点.(画出一个点
为直角顶点.(画出一个点![]() 即可)
即可)

(2)在(1)的条件下,若![]() ,
,![]() ,则点
,则点![]() 的坐标是________.
的坐标是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】发现问题:如图1,直线a∥b,点B、C在直线b上,点D为AC的中点,过点D的直线与a,b分别相交于M、N两点,与BA的延长线交于点P,若△ABC的面积为1,则四边形AMNB的面积为 ;
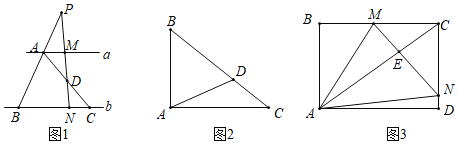
探究问题:如图2,Rt△ABC中,∠DAC=![]() ∠BAC,DA=2,求△ABC面积的最小值;
∠BAC,DA=2,求△ABC面积的最小值;
拓展应用:如图3,矩形花园ABCD的长AD为400米,宽CD为300米,供水点E在小路AC上,且AE=2CE,现想沿BC上一点M和CD上一点N修一条小路MN,使得MN经过E,并在四边形AMCN围城的区域内种植花卉,剩余区域铺设草坪根据项目的要求种植花卉的区域要尽量小.请根据相关数据求出四边形AMCN面积的最小值,及面积取最小时点M、N的位置.(小路的宽忽略不计)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com