
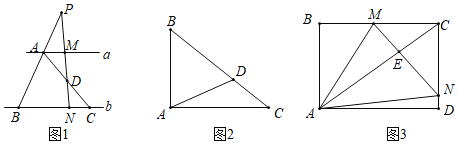
【题目】发现问题:如图1,直线a∥b,点B、C在直线b上,点D为AC的中点,过点D的直线与a,b分别相交于M、N两点,与BA的延长线交于点P,若△ABC的面积为1,则四边形AMNB的面积为 ;
探究问题:如图2,Rt△ABC中,∠DAC=![]() ∠BAC,DA=2,求△ABC面积的最小值;
∠BAC,DA=2,求△ABC面积的最小值;
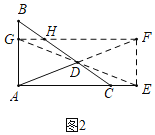
拓展应用:如图3,矩形花园ABCD的长AD为400米,宽CD为300米,供水点E在小路AC上,且AE=2CE,现想沿BC上一点M和CD上一点N修一条小路MN,使得MN经过E,并在四边形AMCN围城的区域内种植花卉,剩余区域铺设草坪根据项目的要求种植花卉的区域要尽量小.请根据相关数据求出四边形AMCN面积的最小值,及面积取最小时点M、N的位置.(小路的宽忽略不计)
【答案】发现问题: S四边形AMNB =1;探究问题:当BC与GE重合时,△ABC的面积最小,最小值为2![]() ;拓展应用:四边形AMCN的面积的最小值=80000平方米,此时CM=CF=GH=
;拓展应用:四边形AMCN的面积的最小值=80000平方米,此时CM=CF=GH=![]() 米,CN=CH=200米
米,CN=CH=200米
【解析】
发现问题:证明△ADM≌△CDN(ASA),即可解决问题;
探究问题:如图2中,延长AD到F,使得DF=DA,作FG⊥AB于G,FE⊥AC交AC的延长线于E,利用矩形是中心对称图形,过对称中心的直线平分矩形的面积解决问题即可;
拓展应用:如图3中,取AE的中点G,作GH⊥CD于H,GF⊥BC于F,连接FH.首先证明S四边形AMCN=3S△CMN,当△CMN的面积最小时,四边形AMCN的面积最小,利用探究问题中的方法解决问题即可.
发现问题:如图1中,
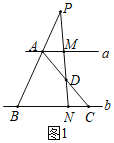
∵a∥b,
∴∠MAD=∠NCD,
∵AD=DC,∠ADM=∠CDN,
∴△ADM≌△CDN(ASA),
∴S△ADM=S△CDN,
∴S四边形AMNB=S△ABC=1,
故答案为1.
探究问题:如图2中,延长AD到F,使得DF=DA,作FG⊥AB于G,FE⊥AC交AC的延长线于E,
∵∠FEA=∠FGA=∠GAE=90°,
∴四边形AEFG是矩形,
∵∠DAC=![]() ∠BAC=30°,AD=DF=2,
∠BAC=30°,AD=DF=2,
∴AF=4,EF=![]() AF=2,AE=
AF=2,AE=![]() EF=2
EF=2![]() ,
,
∴S矩形AEFG=4![]() ,
,
∵矩形AEFG是中心对称图形,D是对称中心,
∴过点D的任意直线平分矩形AEFG的面积,
∴S四边形ACGH=![]() S矩形ABCD=2
S矩形ABCD=2![]() ,
,
∵S△ABC≥S四边形ACHG,
∴S△ABC≥2![]() ,
,
∴当BC与GE重合时,△ABC的面积最小,最小值为2![]() .
.
拓展应用:如图3中,取AE的中点G,作GH⊥CD于H,GF⊥BC于F,连接FH.
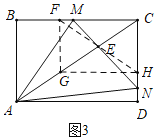
易知四边形GHCF是矩形,
∵AE=2EC,AG=EG,
∴EC=EG,
∴点E在FH上,
∵AC=3EC,
∴S△ACM=3S△ECM,S△ACN=3S△ECN,
∴S四边形AMCN=3S△CMN,
∴当△CMN的面积最小时,四边形AMCN的面积最小,
∵矩形CFGH是中心对称图形,
由探究问题可知:当MN与FH重合时,△MCN的面积最小,
AC=![]() =500(米),
=500(米),
∴CG=![]() ×500=
×500=![]() (米),
(米),
∵GH∥AD,
∴![]() ,
,
∴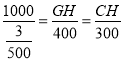 ,
,
∴GH=![]() (米),CH=200(米),
(米),CH=200(米),
∴△MCN的面积的最小值=![]() (平方米),
(平方米),
∴四边形AMCN的面积的最小值=80000(平方米),此时CM=CF=GH=![]() (米),CN=CH=200(米)
(米),CN=CH=200(米)


 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的两边AD、AB的长分别为3、8,边BC落在x轴上,E是DC的中点,连接AE.
(1)若点B坐标为(﹣6,0),求直线AE的表达式;
(2)反比例函数y=![]() (x<0)的图象经过点E,与AB交于点F,若AF﹣AE=2,求反比例函数的表达式;
(x<0)的图象经过点E,与AB交于点F,若AF﹣AE=2,求反比例函数的表达式;
(3)在(2)的条件下,连接矩形ABCD两对边AD与BC的中点M、N,设线段MN与反比例函数图象交于点P,将线段MN沿x轴向右平移n个单位,若MP<NP,直接写出n的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,∠A=30°,BD是⊙O的切线,C为切点,AB与⊙O相交于点E,OC=CD,BC=2,OD与⊙O相交于点F,则弧EF的长为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯公司推出了A,B两种上宽带网的收费方式(详情见下表)
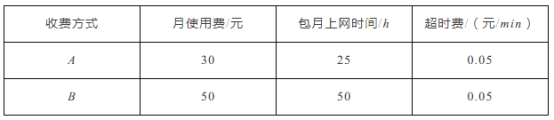
设月上网时间为x h(x为非负整数),请根据表中提供的信息回答下列问题
(1)设方案A的收费金额为y1元,方案B的收费金额为y2元,分别写出y1,y2关于x的函数关系式;
(2)当35<x<50时,选取哪种方式能节省上网费,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一笔直的海岸线l上有A,B两个观测站,A在B的正东方向2千米处.有一艘小船在观测点A北偏西60°的方向上航行,一段时间后,到达点C处,此时,从观测点B测得小船在北偏西15°方向上.求点C与点B之间的距离.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某庄有甲、乙两家草莓采摘园的草莓销售价格相同,春节期间,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为![]() (千克),在甲园所需总费用为
(千克),在甲园所需总费用为![]() (元),在乙园所需总费用为
(元),在乙园所需总费用为![]() (元),
(元),![]() 、
、![]() 与
与![]() 之间的函数关系如图所示.
之间的函数关系如图所示.

(1)甲采摘园的门票是_____元,两个采摘园优惠前的草莓单价是每千克____元;
(2)当![]() 时,求
时,求![]() 与
与![]() 的函数表达式;
的函数表达式;
(3)游客在“春节期间”采摘多少千克草莓时,甲、乙两家采摘园的总费用相同.
查看答案和解析>>
科目:初中数学 来源: 题型:
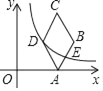
【题目】如图,菱形ABCD的顶点A在x轴的正半轴上,∠C=60°,顶点B,D的纵坐标相同,已知点B的横坐标为7![]() ,若过点D的双曲线y=
,若过点D的双曲线y=![]() (k>0)恰好过边AB的中点E,则k=_____.
(k>0)恰好过边AB的中点E,则k=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
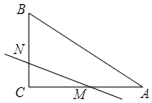
【题目】如图,在Rt△ABC中,∠ACB=90°,BC=6,AC=8,点M是AC边的中点,点N是BC边上的任意一点,若点C关于直线MN的对称点C′恰好落在△ABC的中位线上,则CN的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,对角线AC、BD相交于点O,延长CB至点E,使CE=CA,连接AE,在AB上取一点N,使BN=BE,连接CN并延长,分别交BD、AE于点M、F,连接FO.
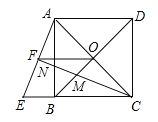
(1) 求证:△ABE ≌△CBN;(2) 求FO的长;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com