练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在一笔直的海岸线l上有A，B两个观测站，A在B的正东方向2千米处．有一艘小船在观测点A北偏西60°的方向上航行，一段时间后，到达点C处，此时，从观测点B测得小船在北偏西15°方向上．求点C与点B之间的距离．（结果保留根号）

    【答案】点C与点B之间的距离为千米．

    【解析】

    作BH⊥AC于H，根据含30°的直角三角形的性质求出BH，根据等腰直角三角形的性质求出BC．

    作BH⊥AC于H，

    由题意得，∠BAC=30°，∠ABC=105°，

    ∴∠C=180°-105°-30°=45°，

    ∵∠AHB=90°，∠BAC=30°，

    ∴BH=AB=1，

    在Rt△BCH中，∠C=45°，

    ∴BC=BH=（千米），

    答：点C与点B之间的距离为千米．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某超市开展早市促销活动，为早到的顾客准备一份简易早餐，餐品有四样：A．韭菜包，B．豆沙包，C．鸡蛋，D．油条．超市约定：“随机发放，早餐一人一份，一份两样，一样一个．”

    （1）按约定，某顾客该天“早餐得到两个鸡蛋”是　 　事件（填“随机”“必然”或“不可能”）：

    （2）请用列表或画树状图的方法，求出某顾客该天“早餐刚好得到一个韭菜包和一根油条”的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，，分别表示使用一种白炽灯和一种节能灯的费用（费用灯的售价电费，单位：元）与照明时间（小时）的函数图象，假设两种灯的使用寿命都是小时，照明效果一样.

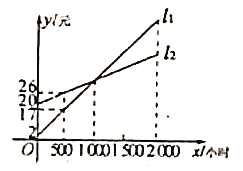
    （1）根据图象分别求出，的函数表达式；

    （2）小亮认为节能灯一定比白炽灯省钱，你是如何想的？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是抛物线y=ax2+bx+c（a≠0）的图象的一部分，抛物线的顶点坐标是A（1，4），与x轴的一个交点是B（3，0），下列结论：①abc＞0；②2a+b=0；③方程ax2+bx+c=4有两个相等的实数根；④抛物线与x轴的另一个交点是（﹣2.0）；⑤x（ax+b）≤a+b，其中正确结论的个数是（　　）

    A. 4个 B. 3个 C. 2个 D. 1个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线的开口向上顶点为P

    （1）若P点坐标为（4，一1），求抛物线的解析式；

    （2）若此抛物线经过（4，一1），当－1≤x≤2时，求y的取值范围（用含a的代数式表示）

    （3）若a＝1，且当0≤x≤1时，抛物线上的点到x轴距离的最大值为6，求b的值

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】发现问题：如图1，直线a∥b，点B、C在直线b上，点D为AC的中点，过点D的直线与a，b分别相交于M、N两点，与BA的延长线交于点P，若△ABC的面积为1，则四边形AMNB的面积为 ；

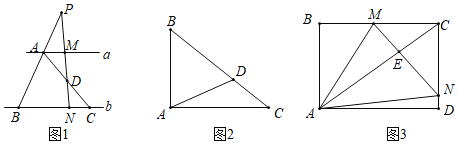
    探究问题：如图2，Rt△ABC中，∠DAC=∠BAC，DA=2，求△ABC面积的最小值；

    拓展应用：如图3，矩形花园ABCD的长AD为400米，宽CD为300米，供水点E在小路AC上，且AE=2CE，现想沿BC上一点M和CD上一点N修一条小路MN，使得MN经过E，并在四边形AMCN围城的区域内种植花卉，剩余区域铺设草坪根据项目的要求种植花卉的区域要尽量小．请根据相关数据求出四边形AMCN面积的最小值，及面积取最小时点M、N的位置．（小路的宽忽略不计）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，AC＝5，AB＝7，BC＝4，点D在边AB上，且AD＝3，动点P从点A出发，以每秒1个单位长度的速度向终点B运动，以PD为边向上作正方形PDMN，设点P运动的时间为t，正方形PDMN与△ABC重叠部分的面积为S．

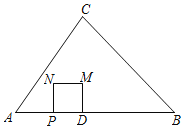
    （1）用含有t的代数式表示线段PD的长

    （2）当点N落在△ABC的边上时，求t的值

    （3）求S与t的函数关系式

    （4）当点P在线段AD上运动时，作点N关于CD的对称点N′，当N′与△ABC的某一个顶点所连的直线平分△ABC的面积时，求t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

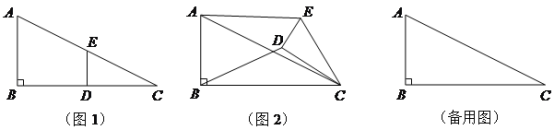
    【题目】（10分）如图1，在Rt△ABC中，∠B=90°，BC=2AB=8，点D，E分别是边BC，AC的中点，连接DE. 将△EDC绕点C按顺时针方向旋转，记旋转角为α.

    （1）问题发现

    ① 当时，；② 当时，

    （2）拓展探究

    试判断：当0°≤α＜360°时，的大小有无变化？请仅就图2的情况给出证明.

    （3）问题解决

    当△EDC旋转至A、D、E三点共线时，直接写出线段BD的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

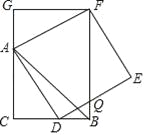
    【题目】如图，CB=CA，∠ACB=90°，点D在边BC上（与B、C不重合），四边形ADEF为正方形，过点F作FG⊥CA，交CA的延长线于点G，连接FB，交DE于点Q，给出以下结论：①AC=FG；②S△FAB：S四边形CBFG=1：2；③∠ABC=∠ABF；④AD2=FQAC，其中正确的结论的个数是_____．

    查看答案和解析>>

    同步练习册答案