
����Ŀ������ABC�У�AC��5��AB��7��BC��4![]() ����D�ڱ�AB�ϣ���AD��3������P�ӵ�A��������ÿ��1����λ���ȵ��ٶ����յ�B�˶�����PDΪ��������������PDMN�����P�˶���ʱ��Ϊt��������PDMN����ABC�ص����ֵ����ΪS��
����D�ڱ�AB�ϣ���AD��3������P�ӵ�A��������ÿ��1����λ���ȵ��ٶ����յ�B�˶�����PDΪ��������������PDMN�����P�˶���ʱ��Ϊt��������PDMN����ABC�ص����ֵ����ΪS��
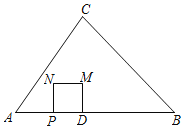
��1���ú���t�Ĵ���ʽ��ʾ�߶�PD�ij�
��2������N������ABC�ı���ʱ����t��ֵ
��3����S��t�ĺ�����ϵʽ
��4������P���߶�AD���˶�ʱ������N����CD�ĶԳƵ�N������N������ABC��ijһ������������ֱ��ƽ����ABC�����ʱ����t��ֵ��
���𰸡���1����0��t��3ʱ��PD��3��t����3��t��7ʱ��PD��t��3����2������������t��ֵΪ![]() s��5s����3��
s��5s����3��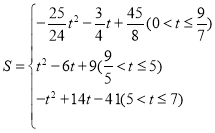 ����4������������t��ֵΪ1s��
����4������������t��ֵΪ1s��![]() s��
s��![]() s��
s��
��������
��1���������������0��t��3ʱ��PD��3��t����3��t��7ʱ��PD��t��3��
��2�����ݣ�1�����������������ƽ�з��߶γɱ��������������t��ֵ��
��3��������PDMN����ABC�ص����ֵ���״����Ϊ����Ρ������Ρ�����Σ�
�ɷ����ηֱ���
����ͼ4�У���0��t��![]() ʱ���ص������������EFPDM��
ʱ���ص������������EFPDM��
����ͼ5��6�У���![]() ��t��5ʱ���ص�������������PDMN��
��t��5ʱ���ص�������������PDMN��
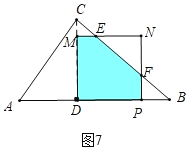
����ͼ7�У���5��t��7ʱ���ص������������EFPDM��
����ƽ�з��߶γɱ����������ֱ���S��t�ĺ�����ϵʽ��
��4�����������������֪��N����CD�ĶԳƵ�N������AC��BC��AB���ߵ������ϣ�
���������,����ͼ�Σ�����ƽ���߷��߶γɱ��������������̼��ɽ�����⣮
��1����ͼ1�У���CD���AB��D��
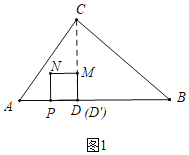
��![]() ����
����![]()
�ɹ��ɶ����ã�![]() ��
��![]() ��
��
![]()
��ã�![]() ����
����![]()
��0��t��3ʱ��PD��3��t��
��3��t��7ʱ��PD��t��3��
��2������ͼ2�У�����N��AC��ʱ��
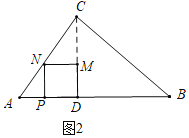
��MN��AD��
![]()
![]()
���![]() .
.
����ͼ3�У�����N��BC��ʱ��
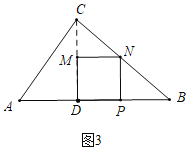
��MN��BD��
![]()
![]()
���t��5
��������������������t��ֵΪ![]() s��5s��
s��5s��
��3��������PDMN����ABC�ص����ֵ��������Ϊ����Ρ������Ρ�����Σ����Է�����������ۣ�
����ͼ4�У���0��t��![]() ʱ���ص������������EFPDM��
ʱ���ص������������EFPDM��
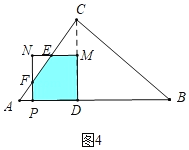
s��S������MDPN��S��NEF����3��t��2��![]()
![]() ��3��t��
��3��t��![]() t��2��
t��2��![]() ��
��
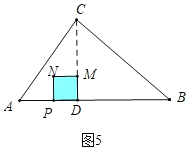
����ͼ5��6�У���![]() ��t��5ʱ���ص�������������PDMN��s��t2��6t+9
��t��5ʱ���ص�������������PDMN��s��t2��6t+9
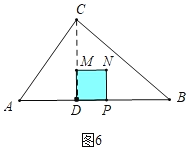
����ͼ7�У���5��t��7ʱ���ص������������EFPDM��s��S������MNPD��S��EFN����t��3��2��![]() [��t��3������7��t��]2����t2+14t��41��
[��t��3������7��t��]2����t2+14t��41��
����������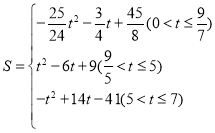 ��
��
��4��N����CD�ĶԳƵ�N������ABC��ijһ������������ֱ��ƽ����ABC�����,
��N��������ABC�������ϣ����Է�����������ۣ�
��ͼ8�У�����N����������AE��ʱ����EK��BC��K��N��J��AB��J��
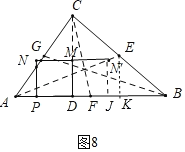
��JN���EK��
![]() ,
,
����![]() ��
��
���t��1��
��ͼ9�У�����N����������BG��ʱ����GK��BC��K��N��J��AB��J��
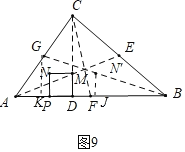
��N��J��GK��
![]() ,
,
![]()
���![]()
��ͼ10�У�����N����������CF��ʱ��
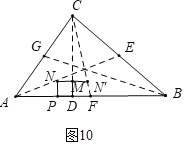
��MN���DF��
![]() ,
,
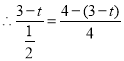 ��
��
���![]()
��������������������t��ֵΪ1s��![]() s��
s��![]() s��
s��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ӳ���Ͷ��һ�����͵��Ӳ�Ʒ��ÿ������ɱ�Ϊ18Ԫ�����������з��֣�ÿ��������![]() ������������۵���
������������۵���![]() ��Ԫ��֮��Ĺ�ϵ���Խ��Ƶؿ���һ�κ���
��Ԫ��֮��Ĺ�ϵ���Խ��Ƶؿ���һ�κ���![]() ������=�ۼ۩�����ɱ���
������=�ۼ۩�����ɱ���
��1��д��ÿ�µ�����![]() ����Ԫ�������۵���
����Ԫ�������۵���![]() ��Ԫ��֮��ĺ�����ϵʽ��
��Ԫ��֮��ĺ�����ϵʽ��
��2��������ز��Ź涨�����ֵ��Ӳ�Ʒ�����۵��۲��ܸ���40Ԫ���������ÿ�µ�����ɱ�������540��Ԫ����ô�����۵���Ϊ����Ԫʱ������ÿ�»�õ���������������Ϊ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
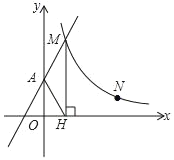
����Ŀ����ͼ��ֱ��y��2x+2��y�ύ��A�㣬�뷴��������y��![]() ��x��0����ͼ���ڵ�M����M��MH��x���ڵ�H����tan��AHO��2��
��x��0����ͼ���ڵ�M����M��MH��x���ڵ�H����tan��AHO��2��
��1����H������꼰k��ֵ��
��2����P��y���ϣ�ʹ��AMP����AMΪ���ĵ��������Σ���ֱ��д����������������P�����ꣻ
��3����N��a��1���Ƿ���������y��![]() ��x��0��ͼ���ϵĵ㣬��Q��m��0����x���ϵĶ��㣬����MNQ�����Ϊ3ʱ���������������������m��ֵ��
��x��0��ͼ���ϵĵ㣬��Q��m��0����x���ϵĶ��㣬����MNQ�����Ϊ3ʱ���������������������m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ��ֱ�ĺ�����l����A��B�����۲�վ��A��B����������2ǧ�״�����һ��С���ڹ۲��A��ƫ��60���ķ����Ϻ��У�һ��ʱ������C������ʱ���ӹ۲��B���С���ڱ�ƫ��15�������ϣ����C���B֮��ľ��룮������������ţ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ҫ��һ��Բ����ˮ�أ�����ˮ�ص����İ�װһ�������ˮͷ���߶�Ϊ![]() m�������ˮ���������߹켣�˶�����ͼ������������ˮƽ����4m���ﵽ��ߣ��߶�Ϊ6m��֮������ˮ�ر�Ե����ô�����ˮ�ص�ֱ��ABΪ____m��
m�������ˮ���������߹켣�˶�����ͼ������������ˮƽ����4m���ﵽ��ߣ��߶�Ϊ6m��֮������ˮ�ر�Ե����ô�����ˮ�ص�ֱ��ABΪ____m��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
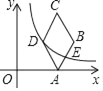
����Ŀ����ͼ������ABCD�Ķ���A��x����������ϣ���C��60�㣬����B��D����������ͬ����֪��B�ĺ�����Ϊ7![]() ��������D��˫����y��
��������D��˫����y��![]() ��k��0��ǡ�ù���AB���е�E����k��_____��
��k��0��ǡ�ù���AB���е�E����k��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����߶�AB�Ƶ�O˳ʱ����ת90���õ��߶�A��B������ôA����2��5���Ķ�Ӧ��A����������
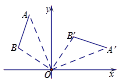
A. ��2��5�� B. ��5��2�� C. ��4�� ![]() �� D. ��
�� D. ��![]() ��4��
��4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
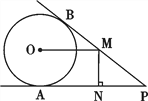
����Ŀ����ͼ��PA��PB�ֱ����O�����ڵ�A��B����M��PB�ϣ���OM��AP��MN��AP������ΪN.
��1����֤��OM = AN��
��2������O�İ뾶R = 3��PA = 9����OM�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����Rt��ABC�͵���Rt��AED�У���ACB=��AED=90�㣬��AD=AC
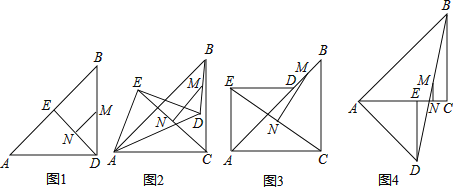
��1�����֣���ͼ1������E��AB���ҵ�C�͵�D�غ�ʱ������M��N�ֱ���DB��EC���е㣬��MN��EC��λ�ù�ϵ���� ����MN��EC��������ϵ���� ��
��2��̽�������ѣ�1��С���еġ�AED�Ƶ�A��תһ���Ƕȣ���ͼ2��ʾ������BD��EC��������DB��EC���е�M��N����MN��EC��λ�ù�ϵ��������ϵ��Ȼ�ܳ�������������������ʱ����ת45��õ���ͼ�Σ�ͼ3��Ϊ������֤��λ�ù�ϵ��������˳ʱ����ת45��õ���ͼ�Σ�ͼ4��Ϊ������֤��������ϵ������������������˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com