
����Ŀ��ij���п�չ���д������Ϊ�絽�Ĺ˿���һ�ݼ�����ͣ���Ʒ��������A���²˰���B����ɳ����C��������D������������Լ������������ţ����һ��һ�ݣ�һ��������һ��һ������
��1����Լ����ij�˿��조��͵õ��������������� ���¼�������������Ȼ�������ܡ�����
��2�������б�����״ͼ�ķ��������ij�˿��조��պõõ�һ���²˰���һ���������ĸ��ʣ�
���𰸡���1�������ܣ���2��![]() ��
��
��������
��1������ȷ���¼�������¼��Ķ�������жϣ���2���������⻭����״ͼ�ó����еȿ��ܵĽ��������պõõ�һ���²˰���һ�������Ľ������Ȼ����ݸ��ʹ�ʽ���㼴�ɣ�
��1��ij�˿��ڸ��조��͵õ������������Dz������¼���
�ʴ�Ϊ:�����ܣ�
��2������״ͼ���£�
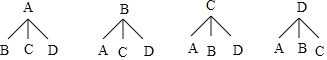
����12�ֵȿ��ܵĽ������������պõõ�һ���²˰���һ��������2�֣�
������պõõ�һ���²˰���һ�������ĸ��ʣ�![]() ��
��![]() ��
��


 �Ͻ�ƽ��У����ϵ�д�
�Ͻ�ƽ��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ࡰ��ѧ��ȤС�顱�Ժ���y��x2��2|x|��ͼ������ʽ�����̽����̽���������£�
��1����ȫ�±�������������ϵ�л���������ͼ��
x | �� | ��3 | �� | ��2 | ��1 | 0 | 1 | 2 |
| 3 | �� |
y | �� | 3 |
| 0 | ��1 | 0 | �� |
��2���۲�ͼ��д���ú���������ͬ���͵����ʣ�
��3����һ��̽������ͼ���֣�
������ͼ����x������ �����㣬���Զ�Ӧ����x2��2|x|��0���� ��ʵ������
������x2��2|x|��2���� ��ʵ������
������x�ķ���x2��2|x|��a��4��ʵ������a��ȡֵ��Χ���� ��
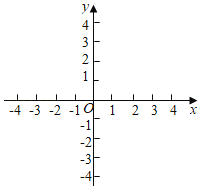
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���� ���ⷢ��
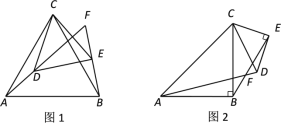
�� ��ͼ1����ABC�͡�CDE��Ϊ�ȱ������Σ�ֱ��AD��ֱ��BE���ڵ�F��
��գ���![]() �Ķ�����________�����߶�AD��BE֮���������ϵΪ________��
�Ķ�����________�����߶�AD��BE֮���������ϵΪ________��
�� ���̽��
��ͼ2����ABC�͡�CDE��Ϊ����ֱ�������Σ�![]() ��
��![]() ��
��![]() ��ֱ��AD��ֱ��BE���ڵ�F�����ж�
��ֱ��AD��ֱ��BE���ڵ�F�����ж�![]() �Ķ������߶�AD��BE֮���������ϵ����˵�����ɣ�
�Ķ������߶�AD��BE֮���������ϵ����˵�����ɣ�
�� �������
��ͼ3���ڡ�ABC�У�![]() ��
��![]() ��
��![]() ����D��AB���ϣ�
����D��AB���ϣ�![]() �ڵ�E��
�ڵ�E��![]() ������ADE���ŵ�A��ƽ������ת����ֱ��д��ֱ��DE������Bʱ����C��ֱ��DE�ľ��룮
������ADE���ŵ�A��ƽ������ת����ֱ��д��ֱ��DE������Bʱ����C��ֱ��DE�ľ��룮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����У�ֻ�������Խ��Խ�ܵ����Ĺ�ע������һ���ڼ䣬С����������������˳���������ѧ���ͼҳ�����ѧ�����ֻ�����Ŀ�����ͳ�����������������µ�ͳ��ͼ��
��1������ε���ļҳ�����������ȫͼ����
��2����ͼ���б�ʾ�ҳ���������Բ�ĽǵĶ�����
��3�����������8��������������������ν��̬�ȵ�ѧ����Լ�ж����ˣ�
��4������ν��ܵ���ļҳ���ѧ����������һ����ǡ����������ν��̬�ȵĸ����Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�![]() ��ֱ��������A����
��ֱ��������A����![]() �����߲�������ȡһ��C������OC����
�����߲�������ȡһ��C������OC����![]() �ڵ�D��BD���ӳ��߽�AC��E������AD.
�ڵ�D��BD���ӳ��߽�AC��E������AD.
��1����֤��![]() ��
��
��2����AB=2��![]() ����AE�ij�.
����AE�ij�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD������AD��AB�ij��ֱ�Ϊ3��8����BC����x���ϣ�E��DC���е㣬����AE��
��1������B����Ϊ����6��0������ֱ��AE�ı���ʽ��
��2������������y��![]() ��x��0����ͼ����E����AB���ڵ�F����AF��AE��2�����������ı���ʽ��
��x��0����ͼ����E����AB���ڵ�F����AF��AE��2�����������ı���ʽ��
��3���ڣ�2���������£����Ӿ���ABCD���Ա�AD��BC���е�M��N�����߶�MN�뷴��������ͼ���ڵ�P�����߶�MN��x������ƽ��n����λ����MP��NP��ֱ��д��n��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ӳ���Ͷ��һ�����͵��Ӳ�Ʒ��ÿ������ɱ�Ϊ18Ԫ�����������з��֣�ÿ��������![]() ������������۵���
������������۵���![]() ��Ԫ��֮��Ĺ�ϵ���Խ��Ƶؿ���һ�κ���
��Ԫ��֮��Ĺ�ϵ���Խ��Ƶؿ���һ�κ���![]() ������=�ۼ۩�����ɱ���
������=�ۼ۩�����ɱ���
��1��д��ÿ�µ�����![]() ����Ԫ�������۵���
����Ԫ�������۵���![]() ��Ԫ��֮��ĺ�����ϵʽ��
��Ԫ��֮��ĺ�����ϵʽ��
��2��������ز��Ź涨�����ֵ��Ӳ�Ʒ�����۵��۲��ܸ���40Ԫ���������ÿ�µ�����ɱ�������540��Ԫ����ô�����۵���Ϊ����Ԫʱ������ÿ�»�õ���������������Ϊ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס���������Լ��ĩ�ǻ���ɽ���ס������˾����ĸ߶�y���ף����ɽʱ��x���֣�֮��ĺ���ͼ����ͼ��ʾ������ͼ�����ṩ����Ϣ����������⣺
(1)��ɽ�������ٶ���ÿ������ ���ף�����A��ʱ�����ĸ߶�bΪ�� ���ף�
(2)�������ٺ��ҵĵ�ɽ�����ٶ��Ǽ�ɽ�����ٶȵ�3����������ҵ�ɽȫ���У������ĸ߶�y���ף����ɽʱ��x���֣�֮��ĺ�����ϵʽ��
(3)��ɽ�ʱ��ʱ���ס������˾����ĸ߶Ȳ�Ϊ70�ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ��ֱ�ĺ�����l����A��B�����۲�վ��A��B����������2ǧ�״�����һ��С���ڹ۲��A��ƫ��60���ķ����Ϻ��У�һ��ʱ������C������ʱ���ӹ۲��B���С���ڱ�ƫ��15�������ϣ����C���B֮��ľ��룮������������ţ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com