
����Ŀ����У�ֻ�������Խ��Խ�ܵ����Ĺ�ע������һ���ڼ䣬С����������������˳���������ѧ���ͼҳ�����ѧ�����ֻ�����Ŀ�����ͳ�����������������µ�ͳ��ͼ��
��1������ε���ļҳ�����������ȫͼ����
��2����ͼ���б�ʾ�ҳ���������Բ�ĽǵĶ�����
��3�����������8��������������������ν��̬�ȵ�ѧ����Լ�ж����ˣ�
��4������ν��ܵ���ļҳ���ѧ����������һ����ǡ����������ν��̬�ȵĸ����Ƕ��٣�

���𰸡���1����ε���ļҳ�������400�ˣ���ȫͼ��������
��2��Բ�ĽǵĶ�����![]()
��3���֡�����ν��̬�ȵ�ѧ����Լ��1.2������
��4��ǡ���ǡ�����ν��̬�ȵĸ�����![]()
��������������(1)��������ͼ�Լ�����ͳ��ͼ�ó�����������;(2)���üҳ����ɡ���ռ���������ó���Բ�ĽǼ���;(3)���ó֡�����ν��̬�ȵ�ѧ����ռ����,�����ó���;(4)���á�����ν��̬�ȵ�����,������������.
���������
��1����������ɵó�: ![]() %=400���ˣ��� �ҳ���������:400-40-80=280(��);
%=400���ˣ��� �ҳ���������:400-40-80=280(��);
��2���ҳ���������Բ�ĽǵĶ���Ϊ�� ![]() ��
��
��3������8����������,�֡�����ν��̬�ȵ�ѧ����Լ��: ![]() ��4������ν��ܵ���ļҳ���ѧ����������һ��,ǡ���ǡ�����ν��̬�ȵĸ�����:
��4������ν��ܵ���ļҳ���ѧ����������һ��,ǡ���ǡ�����ν��̬�ȵĸ�����:
![]()


 ��Ȥ������ҵ���ϿƼ�������ϵ�д�
��Ȥ������ҵ���ϿƼ�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ֱ��������ABC����CΪֱ�ǣ�����ͼ1���ã�ʹ������ԭ�����C�غϣ���֪A��a,3��,B(b,-3),��a+b=8,��������ACB�������
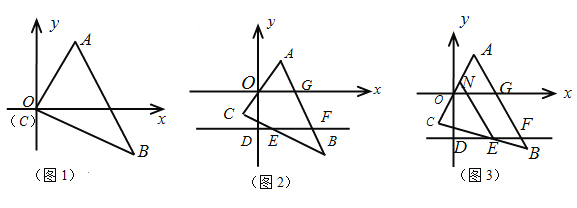
��2����ֱ��������ACB����CΪֱ�ǣ�����ͼ2��ʽ���ã�ʹ�õ�O�ڱ�AC�ϣ�D��y����һ�㣬��D��DF//x�ᣬ��AB��F�㣬AB��x���ڵ�G, BC��DF�ڵ�E, ����AOG=50�㣬���BEF�Ķ�����
��ֱ��������ACB����CΪֱ�ǣ�������ͼ3��ʽ���ã�ʹ�á�C��x����DF֮�䣬NΪAC����һ�㣬�ҡ�NEC+��CEF=180�㣬д����NEF���AOG֮���������ϵ����֤����Ľ��ۡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=x2��4x+3��
��1�����䷽������ͼ��Ķ���C�����ꣻ
��2������ͼ����x��Ľ���A��B�����꣬����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC��D�ǡ�ABC�����ģ�����AD��CD������ADC�Ƶ�A˳ʱ����ת����AEB������ED��
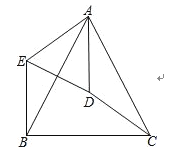
��1����֤����AED�ס�ABC��
��2������BD���ж��ı���AEBD����״��֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���B=��C=30������D��BC����һ�㣬��ADΪֱ������Oǡ��BC�����У���O��A B��E����AC��F����O���ֱ��MN�ֱ��߶�BE��CF��M��N����AM��MB=3��5����FC��AF��ֵΪ�� ��
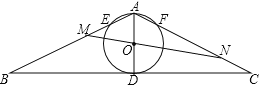
A.3��1 B.5��3 C.2��1 D.5��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ� ��
A. ƽ����������ȵĽ��ǶԶ���
B. ����ֱ����ĵ��ֱ���ϵĵ���߶ν����㵽ֱ�ߵľ���
C. ƽ�������֮�͵���180���������ǻ�Ϊ�ڲ���
D. ƽ���ھ���ֱ����һ��ֻ��һ��ֱ������ֱ֪�ߴ�ֱ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����Сӱ��һ���˿�����������Ϸ��ȥ����С������С�����������ȡһ���ƣ����Żأ���Сӱ��ʣ������������ȡһ�ţ�˭�����������˭�ͻ�ʤ���涨�����С�����˳��Ϊ��2��3��4��5��6��7��8��9��10��J��Q��K��A��������Ĵ�С�뻨ɫ�أ���Ȼ�����˰��������ƶ��Żأ����¿�ʼ��Ϸ��
��1����С���Ѿ�����������Ϊ4��Ȼ��Сӱ���ƣ���ôС����ʤ�ĸ����Ƕ��٣�Сӱ��ʤ�ĸ������Ƕ��٣�
��2����С���Ѿ�����������Ϊ2���������Σ������С���Ѿ�����������ΪA�أ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƻ��������ÿǧ��xԪ��Ҫ�õ�10%���������ƻ���ۼ�Ӧ��ÿǧ��_____Ԫ���ú�x�Ĵ���ʽ��ʾ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com