
【题目】如图,在△ABC中,AB=BC,以AB为直径的⊙O交BC于点D,交AC于点F,过点C作CE∥AB,与过点A的切线相交于点E,连接AD.
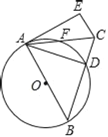
(1)求证:AD=AE.
(2)若AB=10,sin∠DAC=![]() 求AD的长.
求AD的长.
【答案】(1)AD=AE,见解析;(2)AD=8,见解析.
【解析】
(1)由切线的性质和圆周角定理得出∠BAE=90°,∠ADB=∠ADC=90°,由平行线的性质得出∠E=∠ADB,证出∠BCA=∠ACE,证明△ADC≌△AEC,即可得出结论;
(2)连接BF,由圆周角定理得出∠CBF=∠DAC,∠AFB=90°,得出∠CFB=90°,由三角函数求出![]() ,由等腰三角形的性质得出AC=2CF=4
,由等腰三角形的性质得出AC=2CF=4![]() ,在Rt△ACD中,由三角函数求出
,在Rt△ACD中,由三角函数求出![]() ,再由勾股定理即可得出结果.
,再由勾股定理即可得出结果.
解:(1)证明:∵AE与⊙O相切,AB是⊙O的直径
∴∠BAE=90°,∠ADB=90°,
∴∠ADC=90°,
∵CE∥AB,
∴∠BAE+∠E=180°,
∴∠E=90°,
∴∠E=∠ADB,
∵在△ABC中,AB=BC,
∴∠BAC=∠BCA,
∵∠BAC+∠EAC=90°,∠ACE+∠EAC=90°,
∴∠BAC=∠ACE,
∴∠BCA=∠ACE,
在△ADC和△AEC中, ,
,
∴△ADC≌△AEC(AAS),
∴AD=AE;
(2)连接BF,如图所示:

∵∠CBF=∠DAC,∠AFB=90°,
∴∠CFB=90°,sin∠CBF=![]() =sin∠DAC=
=sin∠DAC=![]() ,
,
∵AB=BC=10,
∴CF=2![]() ,
,
∵BF⊥AC,
∴AC=2CF=4![]() ,
,
在Rt△ACD中,sin∠DAC=![]() =
=![]() ,
,
∴CD=![]() ×4
×4![]() =4,
=4,
∴AD=![]() =
=![]() =8.
=8.


科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AB=6,BC=8.点P在矩形ABCD的内部,点E在边BC上,满足△PBE∽△DBC,若△APD是等腰三角形,则PE的长为数___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )

A. B.
B.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自2016年共享单车上市以来,给人们的出行提供了了便利,受到了广大市民的青睐,某公司为了了解员工上下班回家的路线(设路程为x公里)情况,随机抽取了若干名员工进行了问卷调查,现将这些员工的谓查结果分为四个等级,A:0≤x≤3、B:3<x≤6、C:6<x≤9、D:x>9,并将调查结果绘制成如下两个不完整的统计图。
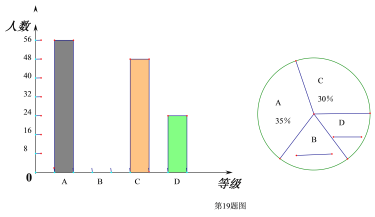
(1)补全上面的条形统计图和扇形统计图中的B D ;
(2)所抽取员工下班路程的中位数落在等级 (填字母)
(3)若该公司有900名员工,为了方便员工上下班,在高峰期时规定路程在6公里以上可优先选择共享单车下斑,请你估算该公司有多少人可以优先选择共享单车。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD的四边BA,CB,DC,AD分别延长至点EF,G,H,使得AE=BF=CG=DH.已知AB=1,BC=2,∠BEF=30°,则tan∠AEH的值为( )
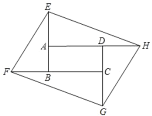
A.2B.![]() C.
C.![]() ﹣1D.
﹣1D.![]() +1
+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2015随州)甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为s(单位:千米),甲行驶的时间为t(单位:小时),s与t之间的函数关系如图所示,有下列结论:
①出发1小时时,甲、乙在途中相遇;
②出发1.5小时时,乙比甲多行驶了60千米;
③出发3小时时,甲、乙同时到达终点;
④甲的速度是乙速度的一半.
其中,正确结论的个数是( )

A. 4B. 3C. 2D. 1
【答案】B
【解析】
试题此题主要考查了一次函数的应用,读函数的图象的关键是理解横、纵坐标表示的意义,根据题意并结合横纵坐标的意义得出辆摩托车的速度,然后再分别分析,即可得出答案.
解:由图象可得:出发1小时,甲、乙在途中相遇,故①正确;
甲骑摩托车的速度为:120÷3=40(千米/小时),设乙开汽车的速度为a千米/小时,
则![]() ,
,
解得:a=80,
∴乙开汽车的速度为80千米/小时,
∴甲的速度是乙速度的一半,故④正确;
∴出发1.5小时,乙比甲多行驶了:1.5×(80﹣40)=60(千米),故②正确;
乙到达终点所用的时间为1.5小时,甲得到终点所用的时间为3小时,故③错误;
∴正确的有①②④,共3个,
故选:B.
考点:一次函数的应用.
【题型】单选题
【结束】
9
【题目】计算:![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图:分别以△ABC的各边为边,在BC边的同侧作等边三角形ABE、等边三角形CBD和等边三角形ACF,连结DE,DF.

(1)试说明四边形DEAF为平行四边形.
(2)当△ABC满足什么条件时,四边形DEAF为矩形?并说明理由;
(3)当△ABC满足什么条件时,四边形DEAF为菱形.直接写出答案 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市预测某饮料有发展前途,用1600元购进一批饮料,面市后果然供不应求,又用6000元购进这批饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若二次购进饮料按同一价格销售,两批全部售完后,获利不少于1200元,那么销售单价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,我们不妨将横坐标,纵坐标均为整数的点称之为“中国结”。
(1)求函数y=![]() x+2的图像上所有“中国结”的坐标;
x+2的图像上所有“中国结”的坐标;
(2)求函数y=![]() (k≠0,k为常数)的图像上有且只有两个“中国结”,试求出常数k的值与相应“中国结”的坐标;
(k≠0,k为常数)的图像上有且只有两个“中国结”,试求出常数k的值与相应“中国结”的坐标;
(3)若二次函数y=![]() (k为常数)的图像与x轴相交得到两个不同的“中国结”,试问该函数的图像与x轴所围成的平面图形中(含边界),一共包含有多少个“中国结”?
(k为常数)的图像与x轴相交得到两个不同的“中国结”,试问该函数的图像与x轴所围成的平面图形中(含边界),一共包含有多少个“中国结”?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com