
【题目】自2016年共享单车上市以来,给人们的出行提供了了便利,受到了广大市民的青睐,某公司为了了解员工上下班回家的路线(设路程为x公里)情况,随机抽取了若干名员工进行了问卷调查,现将这些员工的谓查结果分为四个等级,A:0≤x≤3、B:3<x≤6、C:6<x≤9、D:x>9,并将调查结果绘制成如下两个不完整的统计图。
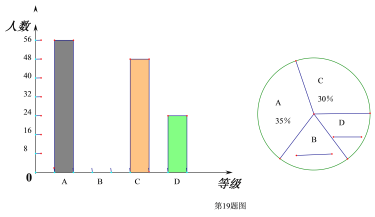
(1)补全上面的条形统计图和扇形统计图中的B D ;
(2)所抽取员工下班路程的中位数落在等级 (填字母)
(3)若该公司有900名员工,为了方便员工上下班,在高峰期时规定路程在6公里以上可优先选择共享单车下斑,请你估算该公司有多少人可以优先选择共享单车。
【答案】(1)B:20%,D:15%,补全统计图见解析;(2)B;(3)405人.
【解析】
(1)根据A等级的人数和所占百分比,求出总人数,然后用总人数减去A,C,D等级的人数可得B等级人数;用B等级人数和D等级人数分别除以总人数,求出所占百分比,即可补全条形统计图和扇形统计图;
(2)根据中位数的定义求解即可;
(3)用样本估计总体的思想解答即可.
解:(1)调查总人数为:56÷35%=160(人),
B等级人数为:160-56-48-24=32(人),
B等级所占百分比为:![]() ,D等级所占百分比为:
,D等级所占百分比为:![]() ,
,
补全统计图如下:
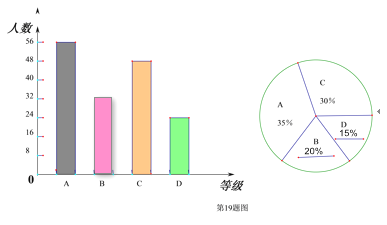
(2)因为调查总人数为160人,所以中位数是第80名和81名的平均数,第80名和81名均在B等级,所以所抽取员工下班路程的中位数落在等级B;
(3)![]() (人),
(人),
即该公司大约有405人可以优先选择共享单车.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,∠C=30°,以边上AC上一点O为圆心,OA为半径作⊙O,⊙O恰好经过边BC的中点D,并与边AC相交于另一点F.

(1)求证:BD是⊙O的切线.
(2)若AB=![]() ,E是半圆
,E是半圆![]() 上一动点,连接AE,AD,DE.
上一动点,连接AE,AD,DE.
填空:
①当![]() 的长度是____________时,四边形ABDE是菱形;
的长度是____________时,四边形ABDE是菱形;
②当![]() 的长度是____________时,△ADE是直角三角形.
的长度是____________时,△ADE是直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中考将近,同学们需要花更多的时间来进行自我反思和总结,消化白天的学习内容,提高学习效率.因此,每个班都在积极地进行自我调整.我校![]() 班和
班和![]() 班的同学也积极响应号召,调查了本班的自习情况以供老师参考.
班的同学也积极响应号召,调查了本班的自习情况以供老师参考.
![]() 班同学在班级抽样调查中,调查了十名同学的学习情况,将这十名同学在一周内每天用于自主复习的总时间四舍五入后,分别记录如下:(单位:分)
班同学在班级抽样调查中,调查了十名同学的学习情况,将这十名同学在一周内每天用于自主复习的总时间四舍五入后,分别记录如下:(单位:分)![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 班的同学采取的普查方式,让每位同学自己写出平均每天的自主复习时间,将数据收集整理后得到以下数据.
班的同学采取的普查方式,让每位同学自己写出平均每天的自主复习时间,将数据收集整理后得到以下数据.
平均数 | 中位数 | 众数 | 极差 | 方差 |
|
|
|
|
|
![]() 班的同学还将自主复习时间分为四大类:第一类为时间小于
班的同学还将自主复习时间分为四大类:第一类为时间小于![]() 分钟以下,第二类为时间大于或等于
分钟以下,第二类为时间大于或等于![]() 分钟且小于
分钟且小于![]() 分钟,第三类为时间大于或等于
分钟,第三类为时间大于或等于![]() 分钟且小于
分钟且小于![]() 分钟,第四类为时间大于或等于
分钟,第四类为时间大于或等于![]() 分钟,并得到如下的扇形图.
分钟,并得到如下的扇形图.

(1)在扇形图中,第一类所对的圆心角度数 .
(2)写出![]() 班被调查同学的以下特征数.
班被调查同学的以下特征数.
平均数 | 中位数 | 众数 | 极差 | 方差 |
|
|
|
(3)从上面的数据,我们可以得到 班的自主复习情况要好一些,其理由为(至少两条):
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南京市某花卉种植基地欲购进甲、乙两种兰花进行培育,每株甲种兰花的成本比每株乙种兰花的成本多100元,且用1200元购进的甲种兰花与用900元购进的乙种兰花数量相同.
(1)求甲、乙两种兰花每株成本分别为多少元?
(2)该种植基地决定在成本不超过30000元的前提下培育甲、乙两种兰花,若培育乙种兰花的株数比甲种兰花的3倍还多10株,求最多购进甲种兰花多少株?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,⊙C的半径为r,给出如下定义:若点P的横、纵坐标均为整数,且到圆心C的距离d≤r,则称P为⊙C 的关联整点.
(1)当⊙O的半径r=2时,在点D(2,-2),E(-1,0),F(0,2)中,为⊙O的关联整点的是 ;
(2)若直线![]() 上存在⊙O的关联整点,且不超过7个,求r的取值范围;
上存在⊙O的关联整点,且不超过7个,求r的取值范围;
(3)⊙C的圆心在x轴上,半径为2,若直线![]() 上存在⊙C的关联整点,求圆心C的横坐标t的取值范围.
上存在⊙C的关联整点,求圆心C的横坐标t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线C1:y=x+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3.0),与y轴交于C(0,-3)
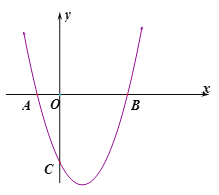
(1)求抛物线C1的表达式;
(2)分别写出抛物线C1关于B点,关于A点的对称抛物线C2, C3的函数表达式
(3)设C1的顶点为D,C2与x轴的另一个交点为A1顶点为D1,C3与x轴的另一个交点为B1,顶点为D2,在以A、B、D、A1、B1、D1、D2这七个点中的四个点为顶点的四边形中,求面积最大的四边形的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,以AB为直径的⊙O交BC于点D,交AC于点F,过点C作CE∥AB,与过点A的切线相交于点E,连接AD.
(1)求证:AD=AE.
(2)若AB=10,sin∠DAC=![]() 求AD的长.
求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现实社会中,塑料袋仍然是白色污染的一部分,为了解塑料袋的使用情况,某校八年级环保小组随机抽取“幸福小区”40户居民家庭,记录了这些家庭某个月丢弃塑料袋的数量(单位:个)如下:
29 39 35 39 39 27 33 35 31 31
32 32 34 31 33 39 38 40 38 42
31 31 38 31 39 27 33 35 40 38
29 39 35 33 39 39 38 42 37 32
请根据上述数据,解答以下问题:
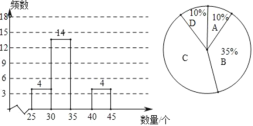
(1)若数据为x,按“组距为5”列出了如下的频数分布表,请将表中空缺的部分补充完整,并补全频数分布直方图;
分组 | 频数 |
A:25≤x<30 | 4 |
B:30≤x<35 | 14 |
C:35≤x<40 | |
D:40≤x<45 | 4 |
合计 | 40 |
(2)根据(1)中的直方图可以看出,这40户居民家庭这个月丢弃塑料袋的个数在 组的家庭最多;(填分组序号)
(3)根据频数分布表,画出了如图所示的扇形统计图,请求出C组对应的扇形圆心角的度数;
(4)若该小区共有1000户居民家庭,请你估计每月丢弃的塑料袋数量不小于30个的家庭户数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:一组邻边相等且对角互补的四边形叫做“邻等对补四边形”
如图1,四边形ABCD中,AB=BC,∠B+∠D=180°(或∠A+∠C=180°),则四边形ABCD叫做“邻等对补四边形”.
概念理解
(1)在以下四种图形中:①平行四边形,②菱形,③矩形,④正方形;一定是“邻等对补四边形”的是 ;(填写序号)
(2)如图2,点A、B、C是网格中格点,请找出两个格点P1,P2,连接P1A、P1C,P2A、P2C画出四边形P1ABC,P2ABC,使四边形P1ABC,P2ABC均为“邻等对补四边形”.
性质证明
(3)如图1,四边形ABCD中,AB=BC,∠A+∠C=180°,连接BD,求证:BD平分∠ADC.
知识运用
(4)如图3,在“邻等对补四边形”ABCD中,满足AB=AD,AB+BC=6,∠ADC=60°时,若2≤BC<3,求四边形ABCD的面积的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com