
����Ŀ���Ͼ���ij������ֲ�����������ס���������������������ÿ����������ijɱ���ÿ�����������ijɱ���100Ԫ������1200Ԫ�����ļ�����������900Ԫ��������������������ͬ��
��1����ס�����������ÿ��ɱ��ֱ�Ϊ����Ԫ��
��2������ֲ���ؾ����ڳɱ�������30000Ԫ��ǰ���������ס����������������������������������ȼ���������3������10�꣬�������������������ꣿ
���𰸡���1��ÿ����������ijɱ�Ϊ400Ԫ��ÿ�����������ijɱ�Ϊ300Ԫ����2��������������20�꣮
��������
��1�������ÿ�����������ijɱ�ΪxԪ������ÿ����������ijɱ���ÿ�����������ijɱ���100Ԫ������֪ÿ����������ijɱ�Ϊ��x+100��Ԫ�������е�����ϵ����1200Ԫ�����ļ�����������=��900Ԫ���������������������ݴ��г����̣�
��2���蹺����������a�꣬�������������������ȼ���������3������10�꣬�ɱ�������30000Ԫ���г�����ʽ����
��1����ÿ�����������ijɱ�ΪxԪ����ÿ����������ijɱ�Ϊ��x+100��Ԫ
�������![]() ��
��
��ã�x��300��
������x��300�Ƿ�ʽ���̵Ľ⣬
��x+100��300+100��400��
��ÿ����������ijɱ�Ϊ400Ԫ��ÿ�����������ijɱ�Ϊ300Ԫ��
��2���蹺����������a��
�������400a+300��3a+10����30000��
��ã�a��![]() ��
��
��a��������
��a�����ֵΪ20��
��������������20�꣮


 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д� �㾦�½̲�ȫ�ܽ��ϵ�д�
�㾦�½̲�ȫ�ܽ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������x�ķ���(a+1)x2+(2a��3)x+a��2��0����������ȵ�ʵ�����ҹ���x�ķ���![]() �Ľ�Ϊ��������������������������a�ĺ���_____��
�Ľ�Ϊ��������������������������a�ĺ���_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
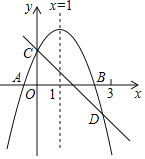
����Ŀ����ͼ��ʾ����֪���κ���y��ax2+bx+c��ͼ����x�ύ��A��B���㣬��y�ύ�ڵ�C���Գ���Ϊֱ��x��1��ֱ��y����x+c��������y��ax2+bx+c����C��D���㣬�����н��ۣ�
��abc��0
��a��b+c��0��
��2a+b+c��0��
��x(ax+b)��a+b��
������ȷ����_____
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�![]() Ϊ����ԭ�㣬�����κ���
Ϊ����ԭ�㣬�����κ���![]() ͼ���ϵĵ�
ͼ���ϵĵ�![]() ����
����![]() ��Ĵ��߽�
��Ĵ��߽�![]() ���ڵ�
���ڵ�![]() .
.
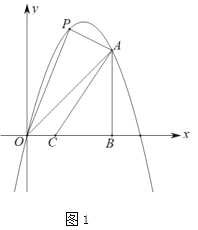
��1����ͼ1��![]() Ϊ�߶�
Ϊ�߶�![]() �Ϸ��������ϵ�һ�㣬��
�Ϸ��������ϵ�һ�㣬��![]() ����ȡ��
����ȡ��![]() ����
����![]() ��
��![]() Ϊ
Ϊ![]() ���ϵ��������㣬��
���ϵ��������㣬��![]() �ڵ�
�ڵ�![]() ���Ϸ���
���Ϸ���![]() ����
����![]() �����ı���
�����ı���![]() ��������ʱ����
��������ʱ����![]() ����Сֵ.
����Сֵ.
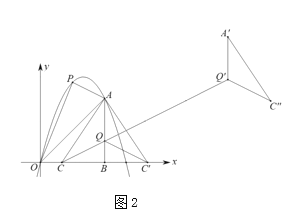
��2����ͼ2����![]() ���߶�
���߶�![]() �ϣ�����
�ϣ�����![]() ����
����![]() ��ֱ��
��ֱ��![]() ���ۣ�
���ۣ�![]() ��Ķ�Ӧ��Ϊ
��Ķ�Ӧ��Ϊ![]() ����
����![]() ������
������![]() ƽ��
ƽ��![]() ����λ��
����λ��![]() ������������ȡһ��
������������ȡһ��![]() ��ʹ����
��ʹ����![]() Ϊ������������ǵ��������Σ���
Ϊ������������ǵ��������Σ���![]() �������.
�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AB=3��BC=4������P��A���������A��B��C�ķ�����AB��BC���ƶ�����PA=x����D��ֱ��PA�ľ���Ϊy����y����x�ĺ���ͼ������ǣ� ��

A. B.
B.
C. D.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
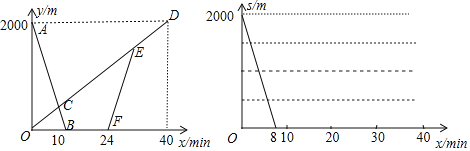
����Ŀ���ס�������֮����һ����ֱ�Ĺ�·l������ʦ�Ӽس����ع�·l����ǰ���ҵأ�ͬʱС�����ҵس����ع�·l�����г�ǰ���أ�С�������ͣ��һ��ʱ�䣬ԭ·ԭ�ٷ��أ�������ʦ������һ���е��ҵأ�������ʦ��صľ���Ϊy1��m����С����صľ���Ϊy2��m��������ʦ��С��֮��ľ���Ϊs��m��������ʦ���ߵ�ʱ��Ϊx��min����y1��y2��x֮��ĺ���ͼ����ͼ1��ʾ��s��x֮��ĺ���ͼ���֣���ͼ2��ʾ��
��1����С�����ҵص��ع�����y2��m����x��min��֮��ĺ�����ϵʽ��
��2��ֱ��д����E�����������ʵ�����壻
��3����ͼ2�У���ȫ����������s��m����x��min��֮��ĺ���ͼ��ע�ؼ�������꣬����ͼ��Ӵ֣���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2016�깲��������������,�����ǵij����ṩ���˱���,�ܵ��˹�������������ij��˾Ϊ���˽�Ա�����°�ؼҵ�·�ߣ���·��Ϊx�������������ȡ��������Ա���������ʾ�����,�ֽ���ЩԱ����ν������Ϊ�ĸ��ȼ���A��0��x��3��B��3��x��6��C��6��x��9��D��x��9,�������������Ƴ�����������������ͳ��ͼ��
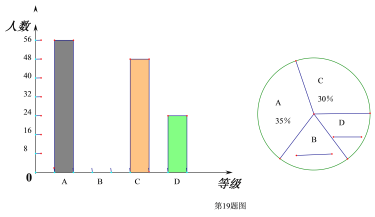
��1����ȫ���������ͳ��ͼ������ͳ��ͼ�е�B D ��
��2������ȡԱ���°�·�̵���λ�����ڵȼ� ������ĸ)
��3�����ù�˾��900��Ա��,Ϊ�˷���Ա�����°�,�ڸ߷���ʱ�涨·����6�������Ͽ�����ѡ���������°�,�������ù�˾�ж����˿�������ѡ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2015���ݣ�����Ħ�г���A��ȥB�أ��ҿ�������B��ȥA�أ�ͬʱ������������ʻ�����Ե����յ��ֹͣ����ס������˼����Ϊs����λ��ǧ�ף�������ʻ��ʱ��Ϊt����λ��Сʱ����s��t֮��ĺ�����ϵ��ͼ��ʾ�������н��ۣ�
�ٳ���1Сʱʱ���ס�����;��������
�ڳ���1.5Сʱʱ���ұȼ���ʻ��60ǧ�ף�
�۳���3Сʱʱ���ס���ͬʱ�����յ㣻
�ܼ��ٶ������ٶȵ�һ�룮
���У���ȷ���۵ĸ����ǣ�������

A. 4B. 3C. 2D. 1
���𰸡�B
��������
���������Ҫ������һ�κ�����Ӧ�ã���������ͼ��Ĺؼ�������ᡢ�������ʾ�����壬�������Ⲣ��Ϻ������������ó���Ħ�г����ٶȣ�Ȼ���ٷֱ���������ɵó��𰸣�
�⣺��ͼ��ɵã�����1Сʱ���ס�����;��������������ȷ��
����Ħ�г����ٶ�Ϊ��120��3=40��ǧ��/Сʱ�������ҿ��������ٶ�Ϊaǧ��/Сʱ��
��![]() ��
��
��ã�a=80��
���ҿ��������ٶ�Ϊ80ǧ��/Сʱ��
�����ٶ������ٶȵ�һ�룬������ȷ��
������1��5Сʱ���ұȼ���ʻ�ˣ�1��5����80��40��=60��ǧ�ף���������ȷ��
�ҵ����յ����õ�ʱ��Ϊ1��5Сʱ���õ��յ����õ�ʱ��Ϊ3Сʱ����������
����ȷ�����٢ڢ�����3����
��ѡ��B��
���㣺һ�κ�����Ӧ�ã�
�����͡���ѡ��
��������
9
����Ŀ�����㣺![]() ______��
______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��������ABCD��AE�۵��õ���AFE���ҵ�Bǡ����DC�ϵĵ�F�غϣ�
��1����֤����ADF�ס�FCE��
��2����tan��CEF��2����tan��AEB��ֵ��
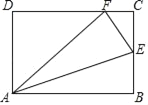
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com