
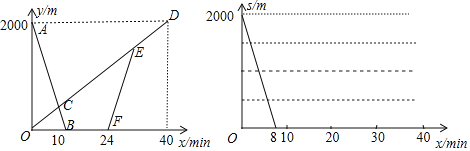
【题目】甲、乙两地之间有一条笔直的公路l,张老师从甲地出发沿公路l步行前往乙地,同时小亮从乙地出发沿公路l骑自行车前往甲地.小亮到达甲地停留一段时间,原路原速返回,追上张老师后两人一起步行到乙地.设张老师与甲地的距离为y1(m),小亮与甲地的距离为y2(m),张老师与小亮之间的距离为s(m),张老师行走的时间为x(min).y1、y2与x之间的函数图象如图1所示,s与x之间的函数图象(部分)如图2所示.
(1)求小亮从乙地到甲地过程中y2(m)与x(min)之间的函数关系式;
(2)直接写出点E的坐标和它的实际意义;
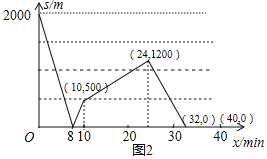
(3)在图2中,补全整个过程中s(m)与x(min)之间的函数图象(标注关键点的坐标,所画图象加粗).
【答案】(1)y2=﹣200x+2000(0≤x≤10);(2)点E(32,1600),张老师出发32min后,被从甲地原路原速返回的小亮追上,此时他们距甲地1600 m;(3)图象见解析.
【解析】
(1)设小亮从乙地到甲地过程中y2(米)与x(分钟)之间的函数关系式为y2=kx+b,由待定系数法根据图象就可以求出解析式;
(2)先根据函数图象求出甲乙的速度,然后与追击问题就可以求出小亮追上小明的时间,就可以求出小亮从甲地返回到与张老师相遇的过程中s(米)与x(分钟)之间的函数关系式 ;
(3)先根据相遇问题建立方程就可以求出a值,10分钟甲、乙走的路程就是相距的距离,14分钟张老师走的路程和小亮追到张老师时的时间就可以补充完图象
(1)设小亮从乙地到甲地过程中y2(m)与x(min)之间的函数关系式为y2=kx+b,
将A(0,2000)、B(10,0)代入到y2=kx+b中,![]() ,解得:
,解得:![]() ,
,
∴y2=﹣200x+2000(0≤x≤10);
(2))由题意,得
张老师的速度为:2000÷40=50米/分,
小亮的速度为:2000÷10=200米/分,
∴小亮从甲地追上张老师的时间为(24×50)÷(20050)=8分钟,
∴24分钟时两人的距离为:S=24×50=1200,32分钟时S=0,距离甲地为50×32=1600米
张老师出发32min后,被从甲地原路原速返回的小亮追上,此时他们距甲地1600 m;
(3))由题意,得
a=2000÷(200+50)=8分钟,
当x=24时,S=1200,
设经过x分钟追上小明,则200x50x=1200,解得x=8,此时的总时间就是24+8=32分钟。
故描出相应的点就可以补全图象,如图


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
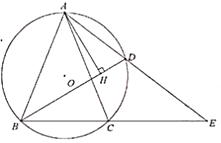
【题目】如图,△ABC内接于⊙O,![]() ,点
,点![]() 为
为![]() 上的动点,且
上的动点,且![]() .
.
(1)求![]() 的长度;
的长度;
(2)在点D运动的过程中,弦AD的延长线交BC的延长线于点E,问ADAE的值是否变化?若不变,请求出ADAE的值;若变化,请说明理由.
(3)在点D的运动过程中,过A点作AH⊥BD,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
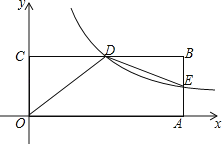
【题目】如图,在平面直角坐标系xOy中,矩形OABC的顶点A在x轴上,顶点C在y轴上,D是BC的中点,过点D的反比例函数图象交AB于E点,连接DE.若OD=5,tan∠COD=![]() .
.
(1)求过点D的反比例函数的解析式;
(2)求△DBE的面积;
(3)x轴上是否存在点P使△OPD为直角三角形?若存在,请直接写出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
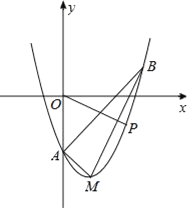
【题目】如图,在平面直角坐标系xOy中,顶点为M的抛物线是由抛物线y=x2﹣3向右平移一个单位后得到的,它与y轴负半轴交于点A,点B在该抛物线上,且横坐标为3.
(1)求点M、A、B坐标;
(2)连结AB、AM、BM,求∠ABM的正切值;
(3)点P是顶点为M的抛物线上一点,且位于对称轴的右侧,设PO与x正半轴的夹角为α,当α=∠ABM时,求P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南京市某花卉种植基地欲购进甲、乙两种兰花进行培育,每株甲种兰花的成本比每株乙种兰花的成本多100元,且用1200元购进的甲种兰花与用900元购进的乙种兰花数量相同.
(1)求甲、乙两种兰花每株成本分别为多少元?
(2)该种植基地决定在成本不超过30000元的前提下培育甲、乙两种兰花,若培育乙种兰花的株数比甲种兰花的3倍还多10株,求最多购进甲种兰花多少株?
查看答案和解析>>
科目:初中数学 来源: 题型:
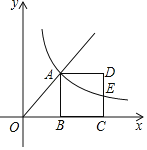
【题目】如图,点A是射线y═![]() (x≥0)上一点,过点A作AB⊥x轴于点B,以AB为边在其右侧作正方形ABCD,过点A的双曲线y=
(x≥0)上一点,过点A作AB⊥x轴于点B,以AB为边在其右侧作正方形ABCD,过点A的双曲线y=![]() 交CD边于点E,则
交CD边于点E,则![]() 的值为_____.
的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线C1:y=x+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3.0),与y轴交于C(0,-3)
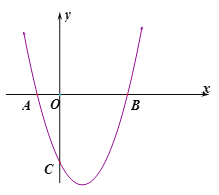
(1)求抛物线C1的表达式;
(2)分别写出抛物线C1关于B点,关于A点的对称抛物线C2, C3的函数表达式
(3)设C1的顶点为D,C2与x轴的另一个交点为A1顶点为D1,C3与x轴的另一个交点为B1,顶点为D2,在以A、B、D、A1、B1、D1、D2这七个点中的四个点为顶点的四边形中,求面积最大的四边形的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
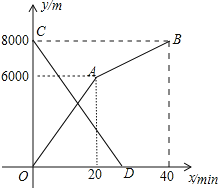
【题目】小明和小亮分别从甲地和乙地同时出发,沿同一条路相向而行,小明开始跑步,中途改为步行,到达乙地恰好用![]() 小亮骑自行车以
小亮骑自行车以![]() 的速度直接到甲地,两人离甲地的路程
的速度直接到甲地,两人离甲地的路程![]() 与各自离开出发地的时间
与各自离开出发地的时间![]() 之间的函数图象如图所示,
之间的函数图象如图所示,
![]() 甲、乙两地之间的路程为______m,小明步行的速度为______
甲、乙两地之间的路程为______m,小明步行的速度为______![]() ;
;
![]() 求小亮离甲地的路程y关于x的函数表达式,并写出自变量x的取值范围;
求小亮离甲地的路程y关于x的函数表达式,并写出自变量x的取值范围;
![]() 求两人相遇的时间.
求两人相遇的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
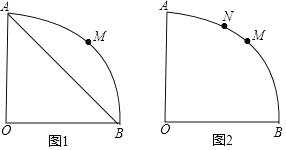
【题目】图1、图2均为圆心角为90°的扇形、请按要求用无刻度的直尺完成下列作图.
(1)在图1中、点M是![]() 的中点、请作出线段AB的垂直平分线;
的中点、请作出线段AB的垂直平分线;
(2)在图2中、点M是![]() 的中点,点N又是
的中点,点N又是![]() 的三等分点,请作出线段0B的垂直平分线.
的三等分点,请作出线段0B的垂直平分线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com