
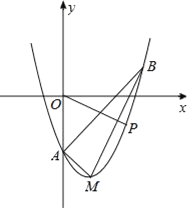
【题目】如图,在平面直角坐标系xOy中,顶点为M的抛物线是由抛物线y=x2﹣3向右平移一个单位后得到的,它与y轴负半轴交于点A,点B在该抛物线上,且横坐标为3.
(1)求点M、A、B坐标;
(2)连结AB、AM、BM,求∠ABM的正切值;
(3)点P是顶点为M的抛物线上一点,且位于对称轴的右侧,设PO与x正半轴的夹角为α,当α=∠ABM时,求P点坐标.
【答案】见解析
【解析】
试题(1)根据平移规律写出抛物线解析式,再求出M、A、B坐标即可.
(2)首先证明△ABE∽△AMF,推出![]() 的值,∠BAM=90°,根据tan∠ABM=
的值,∠BAM=90°,根据tan∠ABM=![]() 即可解决问题.
即可解决问题.
(3)分点P在x轴上方或下方两种情形解决问题.
试题解析:(1)∵抛物线y=x2-3向右平移一个单位后得到的函数解析式为y=(x-1)2-3,
∴顶点M(1,-3),
令x=0,则y=(0-1)2-3=-2,
∴点A(0,-2),
x=3时,y=(3-1)2-3=4-3=1,
∴点B(3,1),
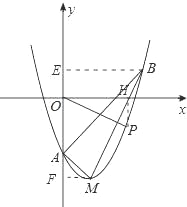
(2)过点B作BE⊥AO于E,过点M作MF⊥AO于M,
∵EB=EA=3,
∴∠EAB=∠EBA=45°,
同理可求∠FAM=∠FMA=45°,
∴△ABE∽△AMF,
∴![]() ,
,
又∵∠BAM=180°-45°×2=90°,
∴tan∠ABM=![]() ,
,
(3)过点P作PH⊥x轴于H,
∵y=(x-1)2-3=x2-2x-2,
∴设点P(x,x2-2x-2),
①点P在x轴的上方时,![]() ,
,
整理得,3x2-7x-6=0,
解得x1=-![]() (舍去),x2=3,
(舍去),x2=3,
∴点P的坐标为(3,1);
②点P在x轴下方时,![]() ,
,
整理得,3x2-5x-6=0,
解得x1=![]() (舍去),x2=
(舍去),x2=![]() ,x=
,x=![]() 时,y=x2-2x-2=
时,y=x2-2x-2=![]() ,
,
∴点P的坐标为(![]() ,
,![]() ),
),
综上所述,点P的坐标为(3,1)或(![]() ,
,![]() ).
).


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
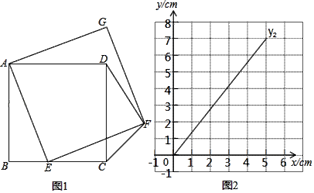
【题目】如图1,正方形ABCD中,AB=5,点E为BC边上一动点,连接AE,以AE为边,在线段AE右侧作正方形![]() ,连接CF、DF.设
,连接CF、DF.设![]() .(当点E与点B重合时,x的值为0),
.(当点E与点B重合时,x的值为0),![]() .小明根据学习函数的经验,对函数
.小明根据学习函数的经验,对函数![]() 随自变量x的变化而变化的规律进行了探究.下面是小明的探究过程,请补充完整:
随自变量x的变化而变化的规律进行了探究.下面是小明的探究过程,请补充完整:
(1)通过取点、画图、测量、观察、计算,得到了x与y1、y2的几组对应值;
x | 0 | 1 | 2 | 3 | 4 | 5 |
| 5.00 | 4.12 | 3.61 | 4.12 | 5.00 | |
| 0 | 1.41 | 2.83 | 4.24 | 5.65 | 7.07 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点![]() ,并画出函数y1,y2的图象;
,并画出函数y1,y2的图象;
(3)结合函数图象2,解决问题:当△CDF为等腰三角形时,BE的长度约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
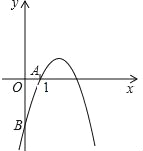
【题目】如图,抛物线y=﹣x2+5x+n经过点A(1,0),与y轴交于点B.
(1)求抛物线的解析式;
(2)P是y轴正半轴上一点,且△PAB是以AB为腰的等腰三角形,试求P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了践行“金山银山,不如绿水青山”的环保理念,重外环保小组的孩子们参与社区公益活动——收集废旧电池,活动开展一个月后,经过统计发现,全组成员平均每人收集了![]() 颗废旧电池,其中,收集数量低于
颗废旧电池,其中,收集数量低于![]() 颗的同学平均每人收集了
颗的同学平均每人收集了![]() 颗,收集数量不低于
颗,收集数量不低于![]() 颗的同学平均每人收集了
颗的同学平均每人收集了![]() 颗,数学王老师发现,若每人再多收集
颗,数学王老师发现,若每人再多收集![]() 颗,则收集数量低于
颗,则收集数量低于![]() 颗的同学平均每人收集了
颗的同学平均每人收集了![]() 颗,收集数量不低于
颗,收集数量不低于![]() 颗的同学平均每人收集了
颗的同学平均每人收集了![]() 颗,并且,该环保小组的人数介于
颗,并且,该环保小组的人数介于![]() 至
至![]() 人.则该环保小组有__________人.
人.则该环保小组有__________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 为坐标原点,过二次函数
为坐标原点,过二次函数![]() 图象上的点
图象上的点![]() ,作
,作![]() 轴的垂线交
轴的垂线交![]() 轴于点
轴于点![]() .
.
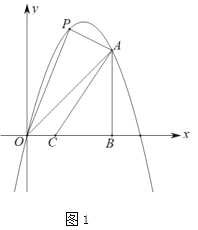
(1)如图1,![]() 为线段
为线段![]() 上方抛物线上的一点,在
上方抛物线上的一点,在![]() 轴上取点
轴上取点![]() ,点
,点![]() 、
、![]() 为
为![]() 轴上的两个动点,点
轴上的两个动点,点![]() 在点
在点![]() 的上方且
的上方且![]() 连接
连接![]() ,当四边形
,当四边形![]() 的面积最大时,求
的面积最大时,求![]() 的最小值.
的最小值.
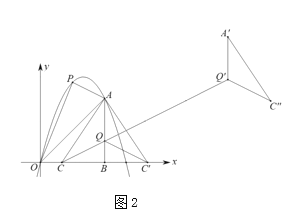
(2)如图2,点![]() 在线段
在线段![]() 上,连接
上,连接![]() ,将
,将![]() 沿直线
沿直线![]() 翻折,
翻折,![]() 点的对应点为
点的对应点为![]() ,将
,将![]() 沿射线
沿射线![]() 平移
平移![]() 个单位得
个单位得![]() ,在抛物线上取一点
,在抛物线上取一点![]() ,使得以
,使得以![]() 为顶点的三角形是等腰三角形,求
为顶点的三角形是等腰三角形,求![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
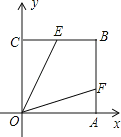
【题目】如图,在正方形OABC中,点B的坐标是(4,4),点E、F分别在边BC、BA上,OE=2![]() .若∠EOF=45°,则F点的纵坐标是( )
.若∠EOF=45°,则F点的纵坐标是( )
A.1B.![]() C.
C.![]() D.
D.![]() ﹣1
﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
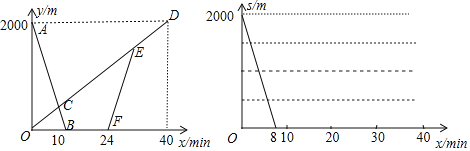
【题目】甲、乙两地之间有一条笔直的公路l,张老师从甲地出发沿公路l步行前往乙地,同时小亮从乙地出发沿公路l骑自行车前往甲地.小亮到达甲地停留一段时间,原路原速返回,追上张老师后两人一起步行到乙地.设张老师与甲地的距离为y1(m),小亮与甲地的距离为y2(m),张老师与小亮之间的距离为s(m),张老师行走的时间为x(min).y1、y2与x之间的函数图象如图1所示,s与x之间的函数图象(部分)如图2所示.
(1)求小亮从乙地到甲地过程中y2(m)与x(min)之间的函数关系式;
(2)直接写出点E的坐标和它的实际意义;
(3)在图2中,补全整个过程中s(m)与x(min)之间的函数图象(标注关键点的坐标,所画图象加粗).
查看答案和解析>>
科目:初中数学 来源: 题型:
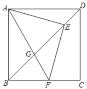
【题目】如图,在正方形ABCD中,AB=3,点E是对角线BD上的一点,连结AE,过点E作EF垂直AE交BC于点F,连结AF,交对角线BD于G.若三角形AED与四边形DEFC的面积之比为3:8,则cos∠GEF=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科技改变着人们的生活,“高铁出行”已成为人们的日常重要交通方式,如今,河南高铁也在发生着日新月异的变化,2018年我省为连接A、B两座城市之间的高铁运行,某工程勘测队在点E处测得城市A在北偏西16°方向上,城市B在北偏东60°方向上,该勘测队沿正东方向行进了7.5km到达点F处,此时测得城市A在北偏西30°方向上,城市B在北偏东30°方向上
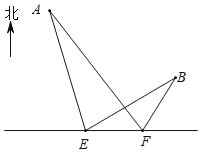
(1)请结合所学的知识判断AB、AE的数量关系,并说明理由;
(2)求城市A和城市B之间的距离为多少公里?(结果精确到1km)(参考数据:![]() ≈1.73,cos74°≈0.28,tan74°≈3.49,sin76°≈0.97,cos76°≈0.24,sin16°≈0.28,cos16°≈0.96)
≈1.73,cos74°≈0.28,tan74°≈3.49,sin76°≈0.97,cos76°≈0.24,sin16°≈0.28,cos16°≈0.96)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com