
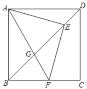
【题目】如图,在正方形ABCD中,AB=3,点E是对角线BD上的一点,连结AE,过点E作EF垂直AE交BC于点F,连结AF,交对角线BD于G.若三角形AED与四边形DEFC的面积之比为3:8,则cos∠GEF=_____.
【答案】![]()
【解析】
连接CE,作EH⊥CD于H,EM⊥BC于M,则四边形EMCH是矩形,得出EM=CH,CM=EH,由正方形的性质得出BC=CD=3,∠ABC=90°,AB=CB,∠ABE=∠CBE=∠BDC=45°,证明△ABE≌△CBE得出EA=EF,∠BAE=∠BCE,同理:△ADE≌△CDE,得出△ADE的面积=△CDE的面积,由已知得出△CDE:△CEF的面积=3:5,证明A、B、F、E四点共圆,由圆周角定理得出∠GEF=∠BAF,∠EFC=∠BAE=∠BCE,得出EF=EC,由等腰三角形的性质得出FM=CM=EH=DH,设FM=CM=EH=DH=x,则FC=2x,EM=HC=3-x,由△CDE:△CEF的面积=3:5得出方程,解得:x=![]() ,得出FC=1,BF=BC-FC=2,由勾股定理求出AF=
,得出FC=1,BF=BC-FC=2,由勾股定理求出AF=![]() ,即可得出结果.
,即可得出结果.
解:连接CE,作EH⊥CD于H,EM⊥BC于M,如图所示:
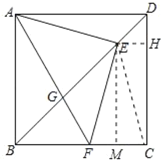
则四边形EMCH是矩形,
∴EM=CH,CM=EH,
∵四边形ABCD是正方形,
∴BC=CD=3,∠ABC=90°,AB=CB,∠ABE=∠CBE=∠BDC=45°,
在△ABE和△CBE中,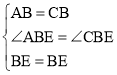 ,
,
∴△ABE≌△CBE(SAS),
∴EA=EF,∠BAE=∠BCE,
同理:△ADE≌△CDE,
∴△ADE的面积=△CDE的面积,
∵△AED与四边形DEFC的面积之比为3:8,
∴△CDE:△CEF的面积=3:5,
∵EF⊥AE,
∴∠AEF=90°,
∴∠ABC+∠AEF=180°,
∴A、B、F、E四点共圆,
∴∠GEF=∠BAF,∠EFC=∠BAE=∠BCE,
∴EF=EC,
∵EM⊥BC,
∴FM=CM=EH=DH,
设FM=CM=EH=DH=x,则FC=2x,EM=HC=3﹣x,
∵△CDE:△CEF的面积=3:5,
∴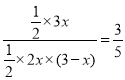 ,
,
解得:x=![]() ,
,
∴FC=1,BF=BC﹣FC=2,
∴AF=![]() ,
,
∴cos∠GEF=cos∠BAF=![]() =
=![]() =
=![]() ;
;
故答案为:![]() .
.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣5,0),对称轴为直线x=﹣2,给出四个结论:①abc>0;②4a﹣b=0;③若点B(﹣3,y1).C(0,y2)为函数图象上的两点,则y1<y2;④a+b+c=0;其中,正确结论的个数是( )
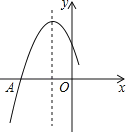
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,顶点为M的抛物线是由抛物线y=x2﹣3向右平移一个单位后得到的,它与y轴负半轴交于点A,点B在该抛物线上,且横坐标为3.
(1)求点M、A、B坐标;
(2)连结AB、AM、BM,求∠ABM的正切值;
(3)点P是顶点为M的抛物线上一点,且位于对称轴的右侧,设PO与x正半轴的夹角为α,当α=∠ABM时,求P点坐标.
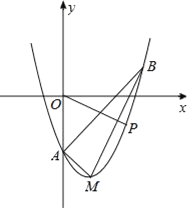
查看答案和解析>>
科目:初中数学 来源: 题型:
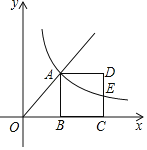
【题目】如图,点A是射线y═![]() (x≥0)上一点,过点A作AB⊥x轴于点B,以AB为边在其右侧作正方形ABCD,过点A的双曲线y=
(x≥0)上一点,过点A作AB⊥x轴于点B,以AB为边在其右侧作正方形ABCD,过点A的双曲线y=![]() 交CD边于点E,则
交CD边于点E,则![]() 的值为_____.
的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线C1:y=x+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3.0),与y轴交于C(0,-3)
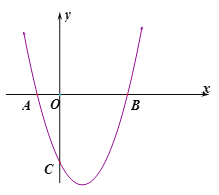
(1)求抛物线C1的表达式;
(2)分别写出抛物线C1关于B点,关于A点的对称抛物线C2, C3的函数表达式
(3)设C1的顶点为D,C2与x轴的另一个交点为A1顶点为D1,C3与x轴的另一个交点为B1,顶点为D2,在以A、B、D、A1、B1、D1、D2这七个点中的四个点为顶点的四边形中,求面积最大的四边形的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABC中,已知AB=BC=10,AC=4![]() ,AD为边BC上的高线,P为边AD上一点,连结BP,E为线段BP上一点,过D、P、E三点的圆交边BC于F,连结EF.
,AD为边BC上的高线,P为边AD上一点,连结BP,E为线段BP上一点,过D、P、E三点的圆交边BC于F,连结EF.
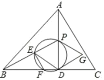
(1)求AD的长;
(2)求证:△BEF∽△BDP;
(3)连结DE,若DP=3,当△DEP为等腰三角形时,求BF的长;
(4)把△DEP沿着直线DP翻折得到△DGP,若G落在边AC上,且DG∥BP,记△APG、△PDG、△GDC的面积分别为S1、S2、S3,则S1:S2:S3的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮分别从甲地和乙地同时出发,沿同一条路相向而行,小明开始跑步,中途改为步行,到达乙地恰好用![]() 小亮骑自行车以
小亮骑自行车以![]() 的速度直接到甲地,两人离甲地的路程
的速度直接到甲地,两人离甲地的路程![]() 与各自离开出发地的时间
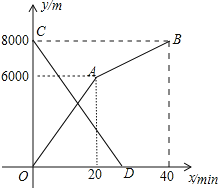
与各自离开出发地的时间![]() 之间的函数图象如图所示,
之间的函数图象如图所示,
![]() 甲、乙两地之间的路程为______m,小明步行的速度为______
甲、乙两地之间的路程为______m,小明步行的速度为______![]() ;
;
![]() 求小亮离甲地的路程y关于x的函数表达式,并写出自变量x的取值范围;
求小亮离甲地的路程y关于x的函数表达式,并写出自变量x的取值范围;
![]() 求两人相遇的时间.
求两人相遇的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
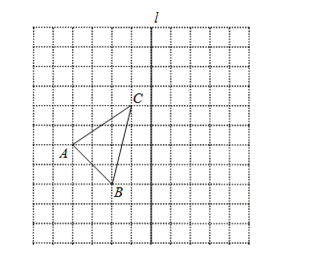
【题目】如图,在![]() 的正方形网格中,每个小正方形的边长都为1,网格中有一个格点
的正方形网格中,每个小正方形的边长都为1,网格中有一个格点![]() (即三角形的顶点都在格点上).
(即三角形的顶点都在格点上).
(1)在图中作出![]() 关于直线l对称的
关于直线l对称的![]() ;(要求A与
;(要求A与![]() ,B与
,B与![]() ,C与
,C与![]() 相对应)
相对应)
(2)作出![]() 绕点C顺时针方向旋转90°后得到的
绕点C顺时针方向旋转90°后得到的![]() ;
;
(3)在(2)的条件下求出线段CB在旋转中所扫过的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
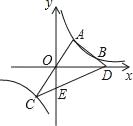
【题目】如图,点A、B在双曲线y=![]() 的第一象限分支上,AO的延长线交第三象限的双曲线于C,AB的延长线与x轴交于点D,连接CD与y轴交于点E,若AB=BD,S△ODE=
的第一象限分支上,AO的延长线交第三象限的双曲线于C,AB的延长线与x轴交于点D,连接CD与y轴交于点E,若AB=BD,S△ODE=![]() ,则k=_____.
,则k=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com