
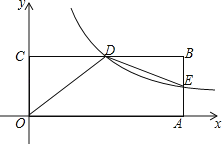
【题目】如图,在平面直角坐标系xOy中,矩形OABC的顶点A在x轴上,顶点C在y轴上,D是BC的中点,过点D的反比例函数图象交AB于E点,连接DE.若OD=5,tan∠COD=![]() .
.
(1)求过点D的反比例函数的解析式;
(2)求△DBE的面积;
(3)x轴上是否存在点P使△OPD为直角三角形?若存在,请直接写出P点的坐标;若不存在,请说明理由.
【答案】(1)![]() (2)3(3)P点的坐标是(4,0)或(
(2)3(3)P点的坐标是(4,0)或(![]() ,0).
,0).
【解析】
(1)由四边形OABC是矩形,得到BC=OA,AB=OC,根据tan∠COD=![]() ,设OC=3x,CD=4x,求出OD=5x=5,OC=3,CD=4,得到D(4,3),代入反比例函数的解析式即可.
,设OC=3x,CD=4x,求出OD=5x=5,OC=3,CD=4,得到D(4,3),代入反比例函数的解析式即可.
(2)根据D点的坐标求出点B,E的坐标即可求出结论;
(3)分类讨论:当∠OPD=90°时,过D作PD⊥x轴于P,点P即为所求,当∠ODP=90°时,根据射影定理即可求得结果.
(1)∵四边形OABC是矩形,
∴BC=OA,AB=OC,
∵tan∠COD=![]() ,
,
∴设OC=3x,CD=4x,
∴OD=5x=5,
∴x=1,
∴OC=3,CD=4,
∴D(4,3),
设过点D的反比例函数的解析式为:y=![]() ,
,
∴k=12,
∴反比例函数的解析式为:y=![]() ;
;
(2)∵点D是BC的中点,
∴B(8,3),
∴BC=8,AB=3,
∵E点在过点D的反比例函数图象上,
∴E(8,![]() ),
),
∴S△DBE=![]() BDBE=
BDBE=![]() =3;
=3;
(3)存在,
∵△OPD为直角三角形,
∴当∠OPD=90°时,PD⊥x轴于P,
∴OP=4,
∴P(4,0),
当∠ODP=90°时,
如图,过D作DH⊥x轴于H,
∴OD2=OHOP,
∴OP=![]() .
.
∴P(![]() ,O),
,O),
∴存在点P使△OPD为直角三角形,
∴P(4,O),(![]() ,O).
,O).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于A、B两点,直线y=
x2+bx+c与x轴交于A、B两点,直线y=![]() x+
x+![]() 经过点A,与抛物线的另一个交点为点C(3,m),线段PQ在线段AB上移动,PQ=1,分别过点P、Q作x轴的垂线,交抛物线于E、F,交直线于D、G.
经过点A,与抛物线的另一个交点为点C(3,m),线段PQ在线段AB上移动,PQ=1,分别过点P、Q作x轴的垂线,交抛物线于E、F,交直线于D、G.
(1)求抛物线的解析式;
(2)设四边形DEFG的面积为S,求S的最大值;
(3)在线段PQ的移动过程中,以D,E,F,G为顶点的四边形是平行四边形时,求点P的坐标.
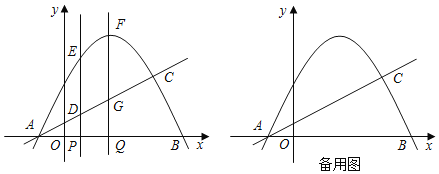
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.在平面直角坐标系中.抛物线y=![]() x2+bx+c与x轴交于A两点,与y轴交于点C,点A的坐标为(﹣1,0),点C的坐标为(0,﹣2).已知点E(m,0)是线段AB上的动点(点E不与点A,B重合).过点E作PE⊥x轴交抛物线于点P.交BC于点F.
x2+bx+c与x轴交于A两点,与y轴交于点C,点A的坐标为(﹣1,0),点C的坐标为(0,﹣2).已知点E(m,0)是线段AB上的动点(点E不与点A,B重合).过点E作PE⊥x轴交抛物线于点P.交BC于点F.
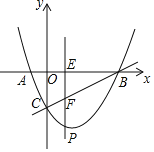
(1)求该抛物线的表达式;
(2)当线段EF,PF的长度比为1:2时,请求出m的值;
(3)是否存在这样的m,使得△BEP与△ABC相似?若存在,求出此时m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
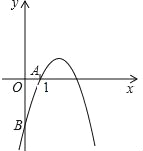
【题目】如图,抛物线y=﹣x2+5x+n经过点A(1,0),与y轴交于点B.
(1)求抛物线的解析式;
(2)P是y轴正半轴上一点,且△PAB是以AB为腰的等腰三角形,试求P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
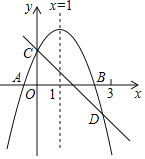
【题目】如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,则下列结论:
①abc>0
②a﹣b+c<0;
③2a+b+c>0;
④x(ax+b)≤a+b;
其中正确的有_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了践行“金山银山,不如绿水青山”的环保理念,重外环保小组的孩子们参与社区公益活动——收集废旧电池,活动开展一个月后,经过统计发现,全组成员平均每人收集了![]() 颗废旧电池,其中,收集数量低于
颗废旧电池,其中,收集数量低于![]() 颗的同学平均每人收集了
颗的同学平均每人收集了![]() 颗,收集数量不低于
颗,收集数量不低于![]() 颗的同学平均每人收集了
颗的同学平均每人收集了![]() 颗,数学王老师发现,若每人再多收集
颗,数学王老师发现,若每人再多收集![]() 颗,则收集数量低于
颗,则收集数量低于![]() 颗的同学平均每人收集了
颗的同学平均每人收集了![]() 颗,收集数量不低于
颗,收集数量不低于![]() 颗的同学平均每人收集了
颗的同学平均每人收集了![]() 颗,并且,该环保小组的人数介于
颗,并且,该环保小组的人数介于![]() 至
至![]() 人.则该环保小组有__________人.
人.则该环保小组有__________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
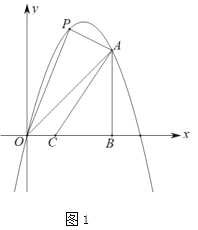
【题目】在平面直角坐标系中,![]() 为坐标原点,过二次函数
为坐标原点,过二次函数![]() 图象上的点
图象上的点![]() ,作
,作![]() 轴的垂线交
轴的垂线交![]() 轴于点
轴于点![]() .
.
(1)如图1,![]() 为线段
为线段![]() 上方抛物线上的一点,在
上方抛物线上的一点,在![]() 轴上取点
轴上取点![]() ,点
,点![]() 、
、![]() 为
为![]() 轴上的两个动点,点
轴上的两个动点,点![]() 在点
在点![]() 的上方且
的上方且![]() 连接
连接![]() ,当四边形
,当四边形![]() 的面积最大时,求
的面积最大时,求![]() 的最小值.
的最小值.
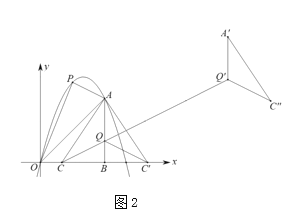
(2)如图2,点![]() 在线段
在线段![]() 上,连接
上,连接![]() ,将
,将![]() 沿直线
沿直线![]() 翻折,
翻折,![]() 点的对应点为
点的对应点为![]() ,将
,将![]() 沿射线
沿射线![]() 平移
平移![]() 个单位得
个单位得![]() ,在抛物线上取一点
,在抛物线上取一点![]() ,使得以
,使得以![]() 为顶点的三角形是等腰三角形,求
为顶点的三角形是等腰三角形,求![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地之间有一条笔直的公路l,张老师从甲地出发沿公路l步行前往乙地,同时小亮从乙地出发沿公路l骑自行车前往甲地.小亮到达甲地停留一段时间,原路原速返回,追上张老师后两人一起步行到乙地.设张老师与甲地的距离为y1(m),小亮与甲地的距离为y2(m),张老师与小亮之间的距离为s(m),张老师行走的时间为x(min).y1、y2与x之间的函数图象如图1所示,s与x之间的函数图象(部分)如图2所示.
(1)求小亮从乙地到甲地过程中y2(m)与x(min)之间的函数关系式;
(2)直接写出点E的坐标和它的实际意义;
(3)在图2中,补全整个过程中s(m)与x(min)之间的函数图象(标注关键点的坐标,所画图象加粗).
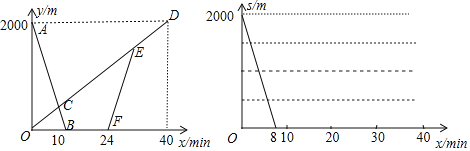
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=﹣x2+3x+m的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴相交于C点.
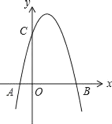
(1)求m的值及C点坐标;
(2)在抛物线的对称轴上是否存在一点M,使得它到B、C两点的距离和最小,若存在,求出此时M点坐标,若不存在,请说明理由;
(3)P为抛物线上一点,它关于直线BC的对称点为Q,当四边形PBQC为菱形时,请直接写出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com