
【题目】如图.在平面直角坐标系中.抛物线y=![]() x2+bx+c与x轴交于A两点,与y轴交于点C,点A的坐标为(﹣1,0),点C的坐标为(0,﹣2).已知点E(m,0)是线段AB上的动点(点E不与点A,B重合).过点E作PE⊥x轴交抛物线于点P.交BC于点F.
x2+bx+c与x轴交于A两点,与y轴交于点C,点A的坐标为(﹣1,0),点C的坐标为(0,﹣2).已知点E(m,0)是线段AB上的动点(点E不与点A,B重合).过点E作PE⊥x轴交抛物线于点P.交BC于点F.
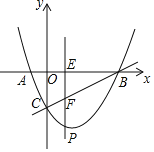
(1)求该抛物线的表达式;
(2)当线段EF,PF的长度比为1:2时,请求出m的值;
(3)是否存在这样的m,使得△BEP与△ABC相似?若存在,求出此时m的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)m=2或4;(3)存在,m的值为0或3.
;(2)m=2或4;(3)存在,m的值为0或3.
【解析】
(1)把点A、点C的坐标代入抛物线表达式,即可求解;
(2)设点E的坐标为(m,0),则点F的坐标为(m,![]() m﹣2),PE=2EF,即:
m﹣2),PE=2EF,即:![]() m﹣2
m﹣2![]() m2
m2![]() m+2=2(2
m+2=2(2![]() m),即可求解;
m),即可求解;
(3)当△BEP与△ABC相似,分∠EPB=∠CAB或∠EPB=∠ABC两种情况,求解即可.
抛物线过点C,则其表达式为:y![]() x2+bx﹣2,
x2+bx﹣2,
将点A坐标代入上式得:0![]() b﹣2,
b﹣2,
解得:b![]() ,
,
故:抛物线的表达式为:y![]() x2
x2![]() x﹣2;
x﹣2;
设直线BC过点C(0,﹣2),设其表达式为:y=kx﹣2,
将点B坐标代入上式得:0=4k﹣2,
解得:k![]() ,则直线BC的表达式为:y
,则直线BC的表达式为:y![]() x﹣2,
x﹣2,
同理直线AC的表达式为:y=﹣2x﹣2,
设点E的坐标为(m,0),则点F的坐标为(m,![]() m﹣2),
m﹣2),
当线段EF,PF的长度比为1:2时,即:PE=2EF,则:![]() m﹣2
m﹣2![]() m2
m2![]() m+2=2(2
m+2=2(2![]() m),解得:m=2或4;
m),解得:m=2或4;
直线BC的表达式为:y![]() x﹣2,直线AC的表达式为:y=﹣2x﹣2,则:BC⊥AC,当△BEP与△ABC相似,则∠EPB=∠CAB,或∠EPB=∠ABC,
x﹣2,直线AC的表达式为:y=﹣2x﹣2,则:BC⊥AC,当△BEP与△ABC相似,则∠EPB=∠CAB,或∠EPB=∠ABC,
即:tan∠EPB=tan∠CAB,或tan∠EPB=tan∠ABC,
当tan∠EPB=tan∠CAB时,即: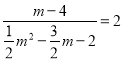 ,
,
解得:m=0或4(舍去m=4),
同理,当tan∠EPB=tan∠ABC,m=3或4(舍去m=4).
故存在,m的值为0或3.


科目:初中数学 来源: 题型:
【题目】下面是“用三角板画圆的切线”的画图过程.
如图1,已知圆上一点A,画过A点的圆的切线.
![]()

画法:(1)如图2,将三角板的直角顶点放在圆上任一点C(与点A不重合)处,使其一直角边经过点A,另一条直角边与圆交于B点,连接AB;
(2)如图3,将三角板的直角顶点与点A重合,使一条直角边经过点B,画出另一条直角边所在的直线AD.
所以直线AD就是过点A的圆的切线.
请回答:该画图的依据是_______________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年1月3日,嫦娥四号探测器自主着落在月球背面,实现人类探测器首次月背软着陆.当时,中国已提前发射的“鹊桥”中继星正在地球、月球延长线上的L2点(第二拉格朗日点)附近,沿L2点的动态平衡轨道飞行,为嫦娥四号着陆器和月球车提供地球、月球中继通信支持,保障嫦娥四号任务的完成与实施.如图,已知月球到地球的平均距离约为38万公里,L2点到月球的平均距离约为6.5万公里.某刻,测得线段CL2与AL2垂直,∠CBL2=56°,则下列计算鹊桥中继星到地球的距离AC方法正确的是( )
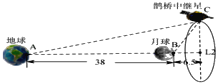
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
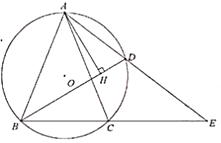
【题目】如图,△ABC内接于⊙O,![]() ,点
,点![]() 为
为![]() 上的动点,且
上的动点,且![]() .
.
(1)求![]() 的长度;
的长度;
(2)在点D运动的过程中,弦AD的延长线交BC的延长线于点E,问ADAE的值是否变化?若不变,请求出ADAE的值;若变化,请说明理由.
(3)在点D的运动过程中,过A点作AH⊥BD,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,∠C=30°,以边上AC上一点O为圆心,OA为半径作⊙O,⊙O恰好经过边BC的中点D,并与边AC相交于另一点F.

(1)求证:BD是⊙O的切线.
(2)若AB=![]() ,E是半圆
,E是半圆![]() 上一动点,连接AE,AD,DE.
上一动点,连接AE,AD,DE.
填空:
①当![]() 的长度是____________时,四边形ABDE是菱形;
的长度是____________时,四边形ABDE是菱形;
②当![]() 的长度是____________时,△ADE是直角三角形.
的长度是____________时,△ADE是直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣5,0),对称轴为直线x=﹣2,给出四个结论:①abc>0;②4a﹣b=0;③若点B(﹣3,y1).C(0,y2)为函数图象上的两点,则y1<y2;④a+b+c=0;其中,正确结论的个数是( )
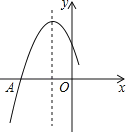
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC为等腰直角三角形,∠ACB=90°,AC=BC,点D和E分别是AC、AB上的点,CE⊥BD,垂足为F
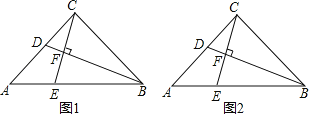
(1)![]()
①求证:D为AC的中点;②计算![]() 的值.
的值.
(2)若![]() ,如图2,则
,如图2,则![]() = (直接写出结果,用k的代数式表示)
= (直接写出结果,用k的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
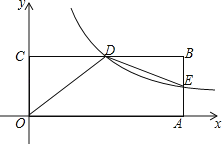
【题目】如图,在平面直角坐标系xOy中,矩形OABC的顶点A在x轴上,顶点C在y轴上,D是BC的中点,过点D的反比例函数图象交AB于E点,连接DE.若OD=5,tan∠COD=![]() .
.
(1)求过点D的反比例函数的解析式;
(2)求△DBE的面积;
(3)x轴上是否存在点P使△OPD为直角三角形?若存在,请直接写出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线C1:y=x+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3.0),与y轴交于C(0,-3)
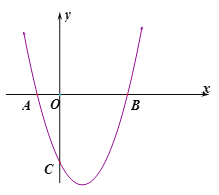
(1)求抛物线C1的表达式;
(2)分别写出抛物线C1关于B点,关于A点的对称抛物线C2, C3的函数表达式
(3)设C1的顶点为D,C2与x轴的另一个交点为A1顶点为D1,C3与x轴的另一个交点为B1,顶点为D2,在以A、B、D、A1、B1、D1、D2这七个点中的四个点为顶点的四边形中,求面积最大的四边形的面积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com