
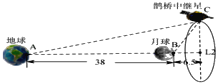
°ĺŐ‚ńŅ°Ņ2019ńÍ1‘¬3»’£¨śŌ∂ūňńļŇŐĹ≤‚∆ų◊‘÷ų◊Ҭš‘ŕ‘¬«ÚĪ≥√ś£¨ ĶŌ÷»ňņŗŐĹ≤‚∆ų ◊īő‘¬Ī≥»Ū◊Ň¬Ĺ£ģĶĪ Ī£¨÷–Ļķ“—ŐŠ«į∑Ę…šĶń°į»Ķ«Ň°Ī÷–ľŐ–«’ż‘ŕĶō«Ú°Ę‘¬«Ú—”≥§ŌŖ…ŌĶńL2Ķ„(Ķŕ∂Ģņ≠łŮņ »’Ķ„)łĹĹŁ£¨—ōL2Ķ„Ķń∂ĮŐ¨∆Ĺļ‚ĻžĶņ∑…––£¨ő™śŌ∂ūňńļŇ◊ҬĹ∆ųļÕ‘¬«Ú≥ĶŐŠĻ©Ķō«Ú°Ę‘¬«Ú÷–ľŐÕ®–Ň÷ß≥÷£¨Ī£’ŌśŌ∂ūňńļŇ»őőŮĶńÕÍ≥…”Ž Ķ ©£ģ»ÁÕľ£¨“—÷™‘¬«ÚĶĹĶō«ÚĶń∆ĹĺýĺŗņŽ‘ľő™38ÕÚĻęņÔ£¨L2Ķ„ĶĹ‘¬«ÚĶń∆ĹĺýĺŗņŽ‘ľő™6.5ÕÚĻęņÔ£ģń≥ŅŐ£¨≤‚Ķ√ŌŖ∂őCL2”ŽAL2īĻ÷Ī£¨°ŌCBL2£Ĺ56°„£¨‘ÚŌ¬Ń–ľ∆ň„»Ķ«Ň÷–ľŐ–«ĶĹĶō«ÚĶńĺŗņŽAC∑Ĺ∑®’ż»∑Ķń «( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
 ŐžŐžŌÚ…Ō“ĽĪĺļ√ĺŪŌĶŃ–īūįł
ŐžŐžŌÚ…Ō“ĽĪĺļ√ĺŪŌĶŃ–īūįł –°—ß…ķ10∑÷÷””¶”√Ő‚ŌĶŃ–īūįł
–°—ß…ķ10∑÷÷””¶”√Ő‚ŌĶŃ–īūįł
| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņő™Ńň√ņĽĮ≥« –Ľ∑ĺ≥£¨ń≥Ĺ÷Ķņ÷ō–řŃň¬∑√ś£¨◊ľĪłĹęņŌĺ…Ķń¬∑Ķ∆ĽĽ≥…LEDŐę—Űń‹¬∑Ķ∆£¨ľ∆ĽģĻļ¬Úļ£¬›ĪŘļÕA◊÷ĪŘŃĹ÷÷–ÕļŇĶńŐę—Űń‹¬∑Ķ∆Ļ≤100÷Ľ£¨ĺ≠Ļż –≥°Ķų≤ť£ļĻļ¬Úļ£¬›ĪŘŐę—Űń‹¬∑Ķ∆1÷Ľ£¨A◊÷ĪŘŐę—Űń‹¬∑Ķ∆2÷ĽĻ≤–Ť2300‘™£ĽĻļ¬Úļ£¬›ĪŘŐę—Űń‹¬∑Ķ∆3÷Ľ£¨A◊÷ĪŘŐę—Űń‹¬∑Ķ∆4÷ĽĻ≤–Ť5400‘™£ģ

£®1£©«ůļ£¬›ĪŘŐę—Űń‹¬∑Ķ∆ļÕA◊÷ĪŘŐę—Űń‹¬∑Ķ∆ĶńĶ•ľŘ£ļ
£®2£©‘ŕ Ķľ Ļļ¬Ú Ī£¨«°∑Í…Őľ“ĽÓ∂Į£¨Ļļ¬Úļ£¬›ĪŘŐę—Űń‹¬∑Ķ∆≥¨Ļż20÷Ľ Ī£¨≥¨ĻżĶń≤Ņ∑÷īÚĺҒؔҼ›£¨A◊÷ĪŘŐę—Űń‹¬∑Ķ∆»ę≤ŅīÚįň’ؔҼ›£Ľ»ŰĻś∂®Ļļ¬ÚĶńļ£¬›ĪŘŐę—Űń‹¬∑Ķ∆Ķń żŃŅ≤Ľ…Ŕ”ŕA◊÷ĪŘŐę—Űń‹¬∑Ķ∆Ķń żŃŅĶń“ĽįŽ£¨«Žń„…Ťľ∆“Ľ÷÷Ļļ¬Ú∑Ĺįł£¨ ĻĶ√◊‹∑—”√◊Ó…Ŕ£¨≤Ę«ů≥Ų◊Ó–°◊‹∑—”√£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
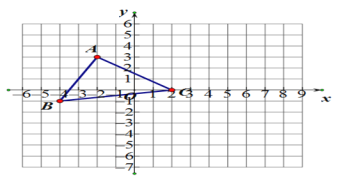
°ĺŐ‚ńŅ°Ņ‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ÷–£¨°ųABCĶń∂•Ķ„◊ÝĪÍ «A£®©Ā2£¨3£©£¨B£®©Ā4£¨©Ā1£©£¨ C£®2£¨0£©£ģĶ„P£®m£¨n£©ő™°ųABCńŕ“ĽĶ„£¨∆Ĺ“∆°ųABCĶ√ĶĹ°ųA1B1C1 £¨ ĻĶ„P£®m£¨n£©“∆ĶĹP£®m+6£¨n+1£©ī¶£ģ
£®1£©Ľ≠≥Ų°ųA1B1C1
£®2£©Ĺę°ųABC»∆◊ÝĪÍĶ„Cńś Ī’Ž–ż◊™90°„Ķ√ĶĹ°ųA2B2C£¨Ľ≠≥Ų°ųA2B2C£Ľ
£®3£©‘ŕ£®2£©ĶńŐűľĢŌ¬«ůBC…®ĻżĶń√śĽż£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨Ň◊őÔŌŖy£Ĺ©Ā![]() x2+bx+c”Žx÷ŠĹĽ”ŕA°ĘBŃĹĶ„£¨÷ĪŌŖy£Ĺ
x2+bx+c”Žx÷ŠĹĽ”ŕA°ĘBŃĹĶ„£¨÷ĪŌŖy£Ĺ![]() x+
x+![]() ĺ≠ĻżĶ„A£¨”ŽŇ◊őÔŌŖĶńŃŪ“ĽłŲĹĽĶ„ő™Ķ„C(3£¨m)£¨ŌŖ∂őPQ‘ŕŌŖ∂őAB…Ō“∆∂Į£¨PQ£Ĺ1£¨∑÷ĪūĻżĶ„P°ĘQ◊ųx÷ŠĶńīĻŌŖ£¨ĹĽŇ◊őÔŌŖ”ŕE°ĘF£¨ĹĽ÷ĪŌŖ”ŕD°ĘG£ģ
ĺ≠ĻżĶ„A£¨”ŽŇ◊őÔŌŖĶńŃŪ“ĽłŲĹĽĶ„ő™Ķ„C(3£¨m)£¨ŌŖ∂őPQ‘ŕŌŖ∂őAB…Ō“∆∂Į£¨PQ£Ĺ1£¨∑÷ĪūĻżĶ„P°ĘQ◊ųx÷ŠĶńīĻŌŖ£¨ĹĽŇ◊őÔŌŖ”ŕE°ĘF£¨ĹĽ÷ĪŌŖ”ŕD°ĘG£ģ
(1)«ůŇ◊őÔŌŖĶńĹ‚őŲ Ĺ£Ľ
(2)…ŤňńĪŖ–őDEFGĶń√śĽżő™S£¨«ůSĶń◊Óīů÷Ķ£Ľ
(3)‘ŕŌŖ∂őPQĶń“∆∂ĮĻż≥Ő÷–£¨“‘D£¨E£¨F£¨Gő™∂•Ķ„ĶńňńĪŖ–ő «∆Ĺ––ňńĪŖ–ő Ī£¨«ůĶ„PĶń◊ÝĪÍ£ģ
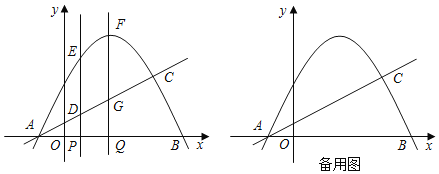
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨Ň◊őÔŌŖ![]() ”Žx÷ŠĹĽ”ŕĶ„A£¨B£¨»ŰĶ„BĶń◊ÝĪÍő™
”Žx÷ŠĹĽ”ŕĶ„A£¨B£¨»ŰĶ„BĶń◊ÝĪÍő™![]() .
.
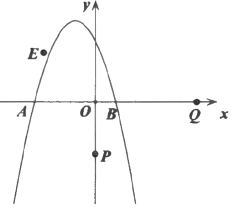
(1)«ůŇ◊őÔŌŖĶńĹ‚őŲ Ĺľį∂•Ķ„◊ÝĪÍ£Ľ
(2)»Ű![]() «
«![]() ÷Š…Ō“ĽĶ„£¨
÷Š…Ō“ĽĶ„£¨![]() £¨ĹęĶ„Q»∆◊ŇĶ„Pńś Ī’Ž∑ĹŌÚ–ż◊™90Ķ√ĶĹĶ„E.
£¨ĹęĶ„Q»∆◊ŇĶ„Pńś Ī’Ž∑ĹŌÚ–ż◊™90Ķ√ĶĹĶ„E.
ĘŔ”√ļ¨tĶń Ĺ◊”ĪŪ ĺĶ„![]() Ķń◊ÝĪÍ£Ľ
Ķń◊ÝĪÍ£Ľ
ĘŕĶĪĶ„E«°ļ√‘ŕł√Ň◊őÔŌŖ…Ō Ī£¨«ůtĶń÷Ķ.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ1£¨’ż∑Ĺ–őABCD÷–£¨AB£Ĺ5£¨Ķ„Eő™BCĪŖ…Ō“Ľ∂ĮĶ„£¨Ń¨Ĺ”AE£¨“‘AEő™ĪŖ£¨‘ŕŌŖ∂őAE”“≤ŗ◊ų’ż∑Ĺ–ő![]() £¨Ń¨Ĺ”CF°ĘDF£ģ…Ť
£¨Ń¨Ĺ”CF°ĘDF£ģ…Ť![]() £ģ(ĶĪĶ„E”ŽĶ„B÷ōļŌ Ī£¨xĶń÷Ķő™0)£¨
£ģ(ĶĪĶ„E”ŽĶ„B÷ōļŌ Ī£¨xĶń÷Ķő™0)£¨![]() £ģ–°√ųłýĺ›—ßŌįļĮ żĶńĺ≠—ť£¨∂‘ļĮ ż
£ģ–°√ųłýĺ›—ßŌįļĮ żĶńĺ≠—ť£¨∂‘ļĮ ż![]() ňś◊‘ĪšŃŅxĶńĪšĽĮ∂ÝĪšĽĮĶńĻś¬…ĹÝ––ŃňŐĹĺŅ£ģŌ¬√ś «–°√ųĶńŐĹĺŅĻż≥Ő£¨«Ž≤Ļ≥šÕÍ’Ż£ļ
ňś◊‘ĪšŃŅxĶńĪšĽĮ∂ÝĪšĽĮĶńĻś¬…ĹÝ––ŃňŐĹĺŅ£ģŌ¬√ś «–°√ųĶńŐĹĺŅĻż≥Ő£¨«Ž≤Ļ≥šÕÍ’Ż£ļ
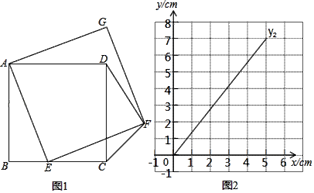
(1)Õ®Ļż»°Ķ„°ĘĽ≠Õľ°Ę≤‚ŃŅ°ĘĻŘ≤ž°Ęľ∆ň„£¨Ķ√ĶĹŃňx”Žy1°Ęy2Ķńľł◊ť∂‘”¶÷Ķ£Ľ
x | 0 | 1 | 2 | 3 | 4 | 5 |
| 5.00 | 4.12 | 3.61 | 4.12 | 5.00 | |
| 0 | 1.41 | 2.83 | 4.24 | 5.65 | 7.07 |
(2)‘ŕÕ¨“Ľ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶxOy÷–£¨√Ť≥Ų≤Ļ»ęļůĶńĪŪ÷–łų◊ť ż÷Ķňý∂‘”¶ĶńĶ„![]() £¨≤ĘĽ≠≥ŲļĮ ży1£¨y2ĶńÕľŌů£Ľ
£¨≤ĘĽ≠≥ŲļĮ ży1£¨y2ĶńÕľŌů£Ľ
(3)ĹŠļŌļĮ żÕľŌů2£¨Ĺ‚ĺŲő Ő‚£ļĶĪ°ųCDFő™Ķ»—Ł»żĹ«–ő Ī£¨BEĶń≥§∂»‘ľő™°° °°cm£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ŰĻō”ŕxĶń∑Ĺ≥Ő(a+1)x2+(2a©Ā3)x+a©Ā2£Ĺ0”–ŃĹłŲ≤ĽŌŗĶ»Ķń Ķłý£¨«“Ļō”ŕxĶń∑Ĺ≥Ő![]() ĶńĹ‚ő™’Ż ż£¨‘Ú¬ķ◊„ŐűľĢĶńňý”–’Ż żaĶńļÕ «_____£ģ
ĶńĹ‚ő™’Ż ż£¨‘Ú¬ķ◊„ŐűľĢĶńňý”–’Ż żaĶńļÕ «_____£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£ģ‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ÷–£ģŇ◊őÔŌŖy£Ĺ![]() x2+bx+c”Žx÷ŠĹĽ”ŕAŃĹĶ„£¨”Žy÷ŠĹĽ”ŕĶ„C£¨Ķ„AĶń◊ÝĪÍő™£®©Ā1£¨0£©£¨Ķ„CĶń◊ÝĪÍő™£®0£¨©Ā2£©£ģ“—÷™Ķ„E£®m£¨0£© «ŌŖ∂őAB…ŌĶń∂ĮĶ„£®Ķ„E≤Ľ”ŽĶ„A£¨B÷ōļŌ£©£ģĻżĶ„E◊ųPE°Õx÷ŠĹĽŇ◊őÔŌŖ”ŕĶ„P£ģĹĽBC”ŕĶ„F£ģ
x2+bx+c”Žx÷ŠĹĽ”ŕAŃĹĶ„£¨”Žy÷ŠĹĽ”ŕĶ„C£¨Ķ„AĶń◊ÝĪÍő™£®©Ā1£¨0£©£¨Ķ„CĶń◊ÝĪÍő™£®0£¨©Ā2£©£ģ“—÷™Ķ„E£®m£¨0£© «ŌŖ∂őAB…ŌĶń∂ĮĶ„£®Ķ„E≤Ľ”ŽĶ„A£¨B÷ōļŌ£©£ģĻżĶ„E◊ųPE°Õx÷ŠĹĽŇ◊őÔŌŖ”ŕĶ„P£ģĹĽBC”ŕĶ„F£ģ
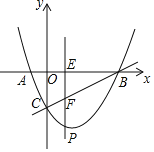
£®1£©«ůł√Ň◊őÔŌŖĶńĪŪīÔ Ĺ£Ľ
£®2£©ĶĪŌŖ∂őEF£¨PFĶń≥§∂»Ī»ő™1£ļ2 Ī£¨«Ž«ů≥ŲmĶń÷Ķ£Ľ
£®3£© «∑Ůīś‘ŕ’‚—ýĶńm£¨ ĻĶ√°ųBEP”Ž°ųABCŌŗň∆£Ņ»Űīś‘ŕ£¨«ů≥Ųīň ĪmĶń÷Ķ£Ľ»Ű≤Ľīś‘ŕ£¨«ŽňĶ√ųņŪ”…£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ÷–£¨![]() ő™◊ÝĪÍ‘≠Ķ„£¨Ļż∂ĢīőļĮ ż
ő™◊ÝĪÍ‘≠Ķ„£¨Ļż∂ĢīőļĮ ż![]() ÕľŌů…ŌĶńĶ„
ÕľŌů…ŌĶńĶ„![]() £¨◊ų
£¨◊ų![]() ÷ŠĶńīĻŌŖĹĽ
÷ŠĶńīĻŌŖĹĽ![]() ÷Š”ŕĶ„
÷Š”ŕĶ„![]() .
.
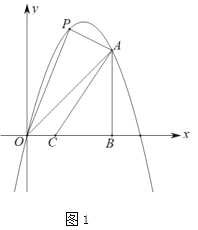
£®1£©»ÁÕľ1£¨![]() ő™ŌŖ∂ő
ő™ŌŖ∂ő![]() …Ō∑ĹŇ◊őÔŌŖ…ŌĶń“ĽĶ„£¨‘ŕ
…Ō∑ĹŇ◊őÔŌŖ…ŌĶń“ĽĶ„£¨‘ŕ![]() ÷Š…Ō»°Ķ„
÷Š…Ō»°Ķ„![]() £¨Ķ„
£¨Ķ„![]() °Ę
°Ę![]() ő™
ő™![]() ÷Š…ŌĶńŃĹłŲ∂ĮĶ„£¨Ķ„
÷Š…ŌĶńŃĹłŲ∂ĮĶ„£¨Ķ„![]() ‘ŕĶ„
‘ŕĶ„![]() Ķń…Ō∑Ĺ«“
Ķń…Ō∑Ĺ«“![]() ѨŔ
ѨŔ![]() £¨ĶĪňńĪŖ–ő
£¨ĶĪňńĪŖ–ő![]() Ķń√śĽż◊Óīů Ī£¨«ů
Ķń√śĽż◊Óīů Ī£¨«ů![]() Ķń◊Ó–°÷Ķ.
Ķń◊Ó–°÷Ķ.
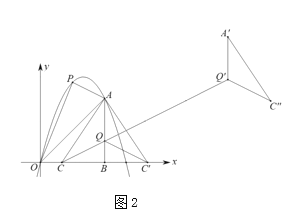
£®2£©»ÁÕľ2£¨Ķ„![]() ‘ŕŌŖ∂ő
‘ŕŌŖ∂ő![]() …Ō£¨Ń¨Ĺ”
…Ō£¨Ń¨Ĺ”![]() £¨Ĺę
£¨Ĺę![]() —ō÷ĪŌŖ
—ō÷ĪŌŖ![]() ∑≠’Ř£¨
∑≠’Ř£¨![]() Ķ„Ķń∂‘”¶Ķ„ő™
Ķ„Ķń∂‘”¶Ķ„ő™![]() £¨Ĺę
£¨Ĺę![]() —ō…šŌŖ
—ō…šŌŖ![]() ∆Ĺ“∆
∆Ĺ“∆![]() łŲĶ•őĽĶ√
łŲĶ•őĽĶ√![]() £¨‘ŕŇ◊őÔŌŖ…Ō»°“ĽĶ„
£¨‘ŕŇ◊őÔŌŖ…Ō»°“ĽĶ„![]() £¨ ĻĶ√“‘
£¨ ĻĶ√“‘![]() ő™∂•Ķ„Ķń»żĹ«–ő «Ķ»—Ł»żĹ«–ő£¨«ů
ő™∂•Ķ„Ķń»żĹ«–ő «Ķ»—Ł»żĹ«–ő£¨«ů![]() Ķ„Ķń◊ÝĪÍ.
Ķ„Ķń◊ÝĪÍ.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ļķľ —ß–£”Ň—° - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com