
【题目】为了美化城市环境,某街道重修了路面,准备将老旧的路灯换成LED太阳能路灯,计划购买海螺臂和A字臂两种型号的太阳能路灯共100只,经过市场调查:购买海螺臂太阳能路灯1只,A字臂太阳能路灯2只共需2300元;购买海螺臂太阳能路灯3只,A字臂太阳能路灯4只共需5400元.

(1)求海螺臂太阳能路灯和A字臂太阳能路灯的单价:
(2)在实际购买时,恰逢商家活动,购买海螺臂太阳能路灯超过20只时,超过的部分打九折优惠,A字臂太阳能路灯全部打八折优惠;若规定购买的海螺臂太阳能路灯的数量不少于A字臂太阳能路灯的数量的一半,请你设计一种购买方案,使得总费用最少,并求出最小总费用.
【答案】(1)海螺臂太阳能路灯的单价为800元/只,![]() 字臂太阳能路灯的单价为750元/只;(2)购买海螺臂太阳能路灯34只,
字臂太阳能路灯的单价为750元/只;(2)购买海螺臂太阳能路灯34只,![]() 字臂太阳能路灯66只可使费用最小,最小费用为65680元
字臂太阳能路灯66只可使费用最小,最小费用为65680元
【解析】
(1)设海螺臂太阳能路灯的单价为![]() 元/只,
元/只,![]() 字臂太阳能路灯的单价为
字臂太阳能路灯的单价为![]() 元/只,找出等量关系,可列二元一次方程,解方程即可
元/只,找出等量关系,可列二元一次方程,解方程即可
(2)设购买海螺臂太阳能路灯![]() 只,
只,![]() 字臂太阳能路灯
字臂太阳能路灯![]() 只,设总费用为
只,设总费用为![]() ,
,
找出等量关系,可列出方程![]()
因为![]() (
(![]() ),所以
),所以![]() ,根据一次函数
,根据一次函数![]() 的性质,可以当
的性质,可以当![]() 取最小整数解,即可求出答案.
取最小整数解,即可求出答案.
解:(1)设海螺臂太阳能路灯的单价为![]() 元/只,
元/只,![]() 字臂太阳能路灯的单价为
字臂太阳能路灯的单价为![]() 元/只,可列方程:
元/只,可列方程:
![]() 解之得:
解之得:![]()
∴海螺臂太阳能路灯的单价为800元/只,![]() 字臂太阳能路灯的单价为750元/只
字臂太阳能路灯的单价为750元/只
(2)设购买海螺臂太阳能路灯![]() 只,
只,![]() 字臂太阳能路灯
字臂太阳能路灯![]() 只,
只,
设总费用为![]() ,则:
,则:
![]()
![]()
![]()
又∵![]() (
(![]() )
)
∴![]()
∵对于一次函数![]() ,
,
![]() ,
,![]() 随
随![]() 的增大而增大,又∵
的增大而增大,又∵![]()
∴当![]() 取最小整数解34时,
取最小整数解34时,![]() 最小
最小![]() (元)
(元)
∴![]() (只),
(只),
∴购买海螺臂太阳能路灯34只,![]() 字臂太阳能路灯66只可使费用最小,最小费用为65680元
字臂太阳能路灯66只可使费用最小,最小费用为65680元


科目:初中数学 来源: 题型:
【题目】如图1,在一张ABCD的纸片中,ABCD的面积为6,DC=3,∠BCD=45°,点P是BD上的一动点(点P与点B,D不重合).现将这张纸片分别沿BD,AP剪成三块,并按图2(注:图2中的①,②是将图1中的①,②翻转背面朝上,再拼接而成的)所示放置
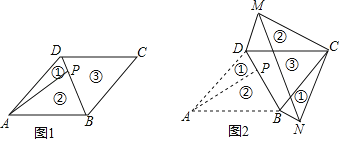
(1)当点P是BD的中点时,求AP的长.
(2)试探究:当点P在BD的什么位置上时,MN的长最小?请求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
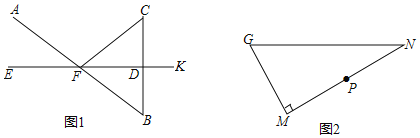
【题目】(1)如图1,已知EK垂直平分BC,垂足为D,AB与EK相交于点F,连接CF.求证:∠AFE=∠CFD.
(2)如图2,在Rt△GMN中,∠M=90°,P为MN的中点.
①用直尺和圆规在GN边上求作点Q,使得∠GQM=∠PQN(保留作图痕迹,不要求写作法);
②在①的条件下,如果∠G=60°,那么Q是GN的中点吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
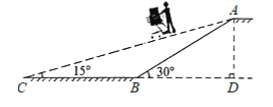
【题目】某市商场为方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯.如图所示,已知原阶梯式自动扶梯![]() 长为
长为![]() ,坡角
,坡角![]() 为30°;改造后的斜坡式自动扶梯的坡角
为30°;改造后的斜坡式自动扶梯的坡角![]() 为15°,改造后的斜坡式自动扶梯水平距离增加了
为15°,改造后的斜坡式自动扶梯水平距离增加了![]() ,请你计算
,请你计算![]() 的长度,(结果精确到
的长度,(结果精确到![]() ,参考数据:
,参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,AB长为半径画弧,交边AD于点;②再分别以B,F为圆心画弧,两弧交于平行四边形ABCD内部的点G处;③连接AG并延长交BC于点E,连接BF,若BF=3,AB=2.5,则AE的长为( )
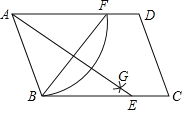
A.2B.4C.8D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了激励学生热爱数学,刻苦钻研,马鞍山市某学校八年级举行了一次数学竞赛,成绩由低到高分为![]() 五个等级.竞赛结束后老师随机抽取了部分学生的成绩情况绘制成如下的条形图和扇形图,请根据提供的信息解答以下问题.
五个等级.竞赛结束后老师随机抽取了部分学生的成绩情况绘制成如下的条形图和扇形图,请根据提供的信息解答以下问题.

![]() 补全条形统计图和统计扇形图.
补全条形统计图和统计扇形图.
![]() 在本次抽样调查中,成绩的众数和中位数分别处于哪个等级?
在本次抽样调查中,成绩的众数和中位数分别处于哪个等级?
![]() 成绩为
成绩为![]() 等级的五个人中有
等级的五个人中有![]() 名男生
名男生![]() 名女生,若从中任选两人,则两人恰好是一男一女的概率为多少?
名女生,若从中任选两人,则两人恰好是一男一女的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月23日是第二十四个“世界读书日“.某校组织读书征文比赛活动,评选出一、二、三等奖若干名,并绘成如图所示的条形统计图和扇形统计图(不完整),请你根据图中信息解答下列问题:
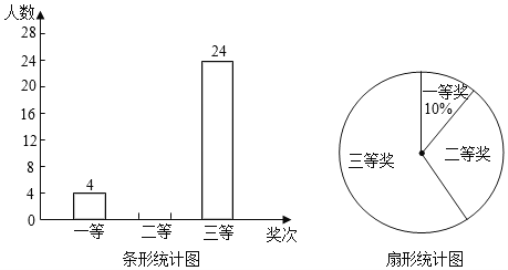
(1)求本次比赛获奖的总人数,并补全条形统计图;
(2)求扇形统计图中“二等奖”所对应扇形的圆心角度数;
(3)学校从甲、乙、丙、丁4位一等奖获得者中随机抽取2人参加“世界读书日”宣传活动,请用列表法或画树状图的方法,求出恰好抽到甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
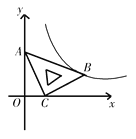
【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),AB=![]() ,点A在y轴上,反比例函数经过点B,求反比例函数解析式______.
,点A在y轴上,反比例函数经过点B,求反比例函数解析式______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把有一条边是另一条边的2倍的梯形叫做“倍边梯形”,在⊙O中,直径AB=2,PQ是弦,若四边形ABPQ是“倍边梯形”,那么PQ的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com