
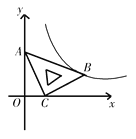
【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),AB=![]() ,点A在y轴上,反比例函数经过点B,求反比例函数解析式______.
,点A在y轴上,反比例函数经过点B,求反比例函数解析式______.
【答案】![]()
【解析】
过点B作BD⊥x轴于点D,在Rt△ABC中利用勾股定理求出AC的长,在Rt△OAC中利用勾股定理求出OA的长,然后证明△OAC≌DCB,可得BD,CD的长,即可得点B的坐标,最后利用待定系数法即可求出反比例函数的解析式.
解:过点B作BD⊥x轴于点D,

在Rt△ABC中,AC=BC,AB=![]() ,
,
由勾股定理可得AC=BC=2,
∵点C的坐标为(1,0),
∴OC=1,
在Rt△OAC中,
OA=![]() =
=![]() =
=![]() .
.
∵∠OCA+∠DCB=90°,∠OCA+∠OAC=90°,
∴∠OAC=∠DCB,
在△OAC和△DCB中,
 ,
,
∴△OAC≌△DCB,
∴CD=OA=![]() ,BD=OC=1,
,BD=OC=1,
∴OD=CD+OC=![]() +1,
+1,
即点B的坐标为(![]() +1,1).
+1,1).
设反比例函数的解析式为y=![]() ,
,
则1=![]() ,
,
解得k=![]() +1,
+1,
所以反比例函数的解析式为y=![]() .
.
故答案为:y=![]() .
.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点A,对点A作如下变换:
第一步:作点A关于x轴的对称点A1;第二步:以O为位似中心,作线段OA1的位似图形OA2,且相似比![]() =q,则称A2是点A的对称位似点.
=q,则称A2是点A的对称位似点.
(1)若A(2,3),q=2,直接写出点A的对称位似点的坐标;
(2)已知直线l:y=kx-2,抛物线C:y=-![]() x2+mx-2(m>0).点N(
x2+mx-2(m>0).点N(![]() ,2k-2)在直线l上.
,2k-2)在直线l上.
①当k=![]() 时,判断E(1,-1)是否是点N的对称位似点,请说明理由;
时,判断E(1,-1)是否是点N的对称位似点,请说明理由;
②若直线l与抛物线C交于点M(x1,y1)(x1≠0),且点M不是抛物线的顶点,则点M的对称位似点是否可能仍在抛物线C上?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了美化城市环境,某街道重修了路面,准备将老旧的路灯换成LED太阳能路灯,计划购买海螺臂和A字臂两种型号的太阳能路灯共100只,经过市场调查:购买海螺臂太阳能路灯1只,A字臂太阳能路灯2只共需2300元;购买海螺臂太阳能路灯3只,A字臂太阳能路灯4只共需5400元.

(1)求海螺臂太阳能路灯和A字臂太阳能路灯的单价:
(2)在实际购买时,恰逢商家活动,购买海螺臂太阳能路灯超过20只时,超过的部分打九折优惠,A字臂太阳能路灯全部打八折优惠;若规定购买的海螺臂太阳能路灯的数量不少于A字臂太阳能路灯的数量的一半,请你设计一种购买方案,使得总费用最少,并求出最小总费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为4,P为BC边上的动点,连接AP,作PQ⊥PA交CD边于点Q.当点P从B运动到C时,线段AQ的中点M所经过的路径长( )
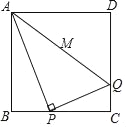
A. 2 B. 1 C. 4 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市A,B两个蔬菜基地得知四川C,D两个灾民安置点分别急需蔬菜240t和260t的消息后,决定调运蔬菜支援灾区,已知A蔬菜基地有蔬菜200t,B蔬菜基地有蔬菜300t,现将这些蔬菜全部调运C,D两个灾区安置点.从A地运往C,D两处的费用分别为每吨20元和25元,从B地运往C,D两处的费用分别为每吨15元和18元.设从B地运往C处的蔬菜为x吨.
(1)请填写下表,并求两个蔬菜基地调运蔬菜的运费相等时x的值;
C | D | 总计/t | |
A | 200 | ||
B | x | 300 | |
总计/t | 240 | 260 | 500 |
(2)设A,B两个蔬菜基地的总运费为w元,求出w与x之间的函数关系式,并求
总运费最小的调运方案;
(3)经过抢修,从B地到C处的路况得到进一步改善,缩短了运输时间,运费每吨减少m元(m>0),其余线路的运费不变,试讨论总运费最小的调动方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】立定跳远是体育中考选考项目之一,体育课上老师记录了某同学的一组立定跳远成绩如表:
成绩(m) | 2.3 | 2.4 | 2.5 | 2.4 | 2.4 |
则下列关于这组数据的说法,正确的是( )
A.众数是2.3B.平均数是2.4
C.中位数是2.5D.方差是0.01
查看答案和解析>>
科目:初中数学 来源: 题型:
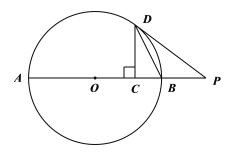
【题目】如图,点D在⊙O上,过点D的切线交直径AB的延长线于点P,DC⊥AB于点C.
(1)求证:DB平分∠PDC;
(2)如果DC = 6,![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
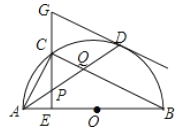
【题目】如图,在![]() 中,
中,![]() 是直径,点
是直径,点![]() 是
是![]() 上一点,点
上一点,点![]() 是
是![]() 的中点,
的中点,![]() 于点
于点![]() ,过点
,过点![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,分别交
,分别交![]() 于点
于点![]() ,连接
,连接![]() ,交于下列结论:
,交于下列结论:
①![]() ;
;
②![]() ;
;
③点![]() 是
是![]() 的外心,
的外心,
④![]()
其中正确结论是_________________(只需填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线y=ax2+bx+3=0(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C
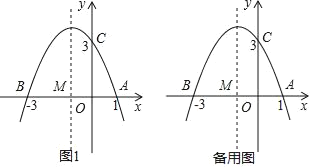
(1)求抛物线的解析式;
(2)设抛物线的对称轴与x轴交于点M,请问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由;
(3)在抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com