
【题目】某市A,B两个蔬菜基地得知四川C,D两个灾民安置点分别急需蔬菜240t和260t的消息后,决定调运蔬菜支援灾区,已知A蔬菜基地有蔬菜200t,B蔬菜基地有蔬菜300t,现将这些蔬菜全部调运C,D两个灾区安置点.从A地运往C,D两处的费用分别为每吨20元和25元,从B地运往C,D两处的费用分别为每吨15元和18元.设从B地运往C处的蔬菜为x吨.
(1)请填写下表,并求两个蔬菜基地调运蔬菜的运费相等时x的值;
C | D | 总计/t | |
A | 200 | ||
B | x | 300 | |
总计/t | 240 | 260 | 500 |
(2)设A,B两个蔬菜基地的总运费为w元,求出w与x之间的函数关系式,并求
总运费最小的调运方案;
(3)经过抢修,从B地到C处的路况得到进一步改善,缩短了运输时间,运费每吨减少m元(m>0),其余线路的运费不变,试讨论总运费最小的调动方案.
【答案】(1)见解析;(2)w=2x+9200,方案见解析;(3)0<m<2时,(2)中调运方案总运费最小;m=2时,在40x240的前提下调运方案的总运费不变;2<m<15时,x=240总运费最小.
【解析】
(1)根据题意可得解.
(2)w与x之间的函数关系式为:w=20(240x)+25(x40)+15x+18(300x);列不等式组解出40≤x≤240,可由w随x的增大而增大,得出总运费最小的调运方案.
(3)根据题意得出w与x之间的函数关系式,然后根据m的取值范围不同分别分析得出总运费最小的调运方案.
解:(1)填表:
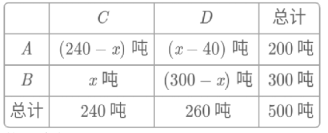
依题意得:20(240x)+25(x40)=15x+18(300x).
解得:x=200.
(2)w与x之间的函数关系为:w=20(240x)+25(x40)+15x+18(300x)=2x+9200.
依题意得: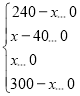
∴40x240
在w=2x+9200中,∵2>0,
∴w随x的增大而增大,
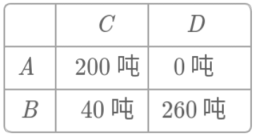
故当x=40时,总运费最小,
此时调运方案为如表.
(3)由题意知w=20(240x)+25(x40)+(15-m)x+18(300x)=(2m)x+9200
∴0<m<2时,(2)中调运方案总运费最小;
m=2时,在40x240的前提下调运
方案的总运费不变;
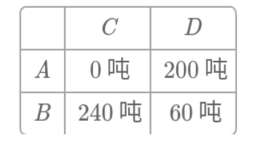
2<m<15时,x=240总运费最小,
其调运方案如表二.


科目:初中数学 来源: 题型:
【题目】随着科技的进步,信息技术越来越发达,人民获得社会新闻信息的途径日益增多,为了解常德市民“获取新闻的最主要途径”,某报社记者在全市城区范围内随机抽取了n名市民,对其获取新闻的最主要途径进行问卷调查.问卷中的途径有:A.电脑上网;B.手机上网;C.电视;D.报纸;E.其他.每位市民在问卷调查时都按要求只选择了其中一种最主要的途径.记者收回了全部问卷后,将收集到的数据整理并绘制成如图不完整的统计图.

根据以上信息解答下列问题:
(l)求n的值.
(2)请补全条形统计图.
(3)根据统计结果,估计常德市城区80万人中.将B途径作为“获取新闻的最主要途径”的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化简
(1)![]() mn﹣4mn;
mn﹣4mn;
(2)3a2﹣2a﹣a2﹣4﹣6a+9;
(3)4(x2﹣5x)﹣5(2x2+3x);
(4)3x2﹣[7x﹣(4x﹣3)﹣2x2]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接“五·一”小长假的购物高峰,某运动品牌服装专卖店准备购进甲、乙两种服装,甲种服装每件进价l80元,售价320元;乙种服装每件进价l50元,售价280元.
(1)若该专卖店同时购进甲、乙两种服装共200件,恰好用去32400元,求购进甲、乙两种服装各多少件?
(2)该专卖店为使甲、乙两种服装共200件的总利润(利润=售价一进价)不少于26700元, 且不超过26800元,则该专卖店有几种进货方案?
(3)在(2)的条件下,专卖店准备在5月1日当天对甲种服装进行优惠促销活动,决定对甲种服装每件优惠a(0<a<20)元出售,乙种服装价格不变.那么该专卖店要获得最大利润应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知代数式A=x2+3xy+x﹣12,B=2x2﹣xy+4y﹣1
(1)当x=y=﹣2时,求2A﹣B的值;
(2)若2A﹣B的值与y的取值无关,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在解决数学问题的过程中,我们常用到“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答题目后提出的“探究”.
(提出问题)三个有理数a,b,c,满足![]() ,求
,求![]() 的值.
的值.
(解决问题).
解:由题意得,a,b,c三个有理数都为正数或其中一个为正数,另两个为负数.
①当a,b,c都是正数,即![]() ,
,![]() ,
,![]() 时,则
时,则![]() (备注:一个非零数除以它本身等于1,如
(备注:一个非零数除以它本身等于1,如![]() ,则
,则![]() ,
,![]() )
)
②当a,b,c有一个为正数,另两个为负数时,设![]() ,
,![]() ,
,![]() ,
,
则![]() .
.
(备注:一个非零数除以它的相反数等于-1,如:![]() ,则
,则![]() ).
).
所以![]() 的值为3或一1.
的值为3或一1.
(探究)请根据上面的解题思路解答下面的问题:
(1)三个有理数a,b,c满足![]() ,求
,求![]() 的值;
的值;
(2)已知![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知命题“若 a>b,则 a2>b2”.
(1)此命题是真命题还是假命题?若是真命题,请给予证明;若是假命题,请举出一个 反例.
(2)写出此命题的逆命题,并判断此逆命题的真假;若是真命题,请给予证明;若是假 命题,请举出一个反例.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划投入50万元,开发并生产甲乙两种产品,根据市场调查预计甲产品的年获利y1(万元)与投入资金x(万元)成正比例,乙产品的年获利y2(万元)与投入资金x(万元)的平方成正比例,设该公司投入乙产品x(万元),两种产品的年总获利为y万元(x≥0),得到了表中的数据.
x(万元) | 20 | 30 |
y(万元) | 10 | 13 |
(1)求y与x的函数关系式;
(2)该公司至少可获得多少利润?请你利用所学的数学知识对该公司投入资金的分配提出合理化建
议,使他能获得最大利润,并求出最大利润是多少?
(3)若从年总利润扣除投入乙产品资金的a倍(a≤1)后,剩余利润随x增大而减小,求a的取值
范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com