
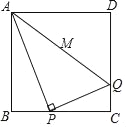
【题目】正方形ABCD的边长为4,P为BC边上的动点,连接AP,作PQ⊥PA交CD边于点Q.当点P从B运动到C时,线段AQ的中点M所经过的路径长( )
A. 2 B. 1 C. 4 D. ![]()
【答案】B
【解析】
分析: 由题意知:PQ⊥AP,即:∠APB+∠QPC=90°,∠BAP+∠APB=180°-∠B=90°,所以∠QPC=∠BAP,又∠B=∠C,即:△ABP∽△PCQ,由相似三角形的性质可得:![]() =
=![]() ,CQ=
,CQ=![]() ×BP,又BP=x,PC=BC-BP=4-x,AB=4,将其代入该式求出CQ的值即可,利用“配方法”求该函数的最大值.易知点O的运动轨迹是O′→O→O′,CQ最大时,OO′=
×BP,又BP=x,PC=BC-BP=4-x,AB=4,将其代入该式求出CQ的值即可,利用“配方法”求该函数的最大值.易知点O的运动轨迹是O′→O→O′,CQ最大时,OO′=![]() CQ=
CQ=![]() .
.
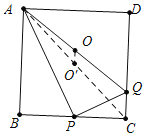
详解: 如图,连接AC,设AC的中点为O′,AQ的中点为O.设BP的长为xcm,CQ的长为ycm.
∵四边形ABCD是正方形,
∴∠B=∠C=90°
∵PQ⊥AP,
∴∠APB+∠QPC=90°
∠APB+∠BAP=90°
∴∠BAP=∠QPC
∴△ABP∽△PCQ
∴![]() =
=![]() ,即
,即![]() ,
,
∴y=-![]() x2+x=-
x2+x=-![]() (x-2)2+1(0<x<4);
(x-2)2+1(0<x<4);
∴当x=2时,y有最大值1cm.
易知点O的运动轨迹是O′→O→O′,CQ最大时,OO′=![]() CQ=
CQ=![]() ,
,
∴点O的运动轨迹的路径的长为2OO′=1,
故答案为1.
点睛: 本题主要考查正方形的性质、二次函数的应用、三角形的中位线定理等知识,关键在于理解题意运用三角形的相似性质求出y与x之间的函数关系,学会探究点O的运动轨迹.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在梯形中![]() 中,
中,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一动点,设
边上一动点,设![]() 的长为
的长为![]() .
.
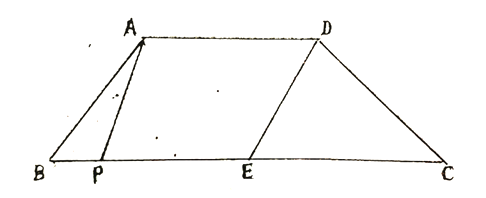
(1)当![]() 的值为多少时,以点
的值为多少时,以点![]() 为顶点的三角形为直角三角形;
为顶点的三角形为直角三角形;
(2)当![]() 的值为多少时,以点
的值为多少时,以点![]() 为顶点的四边形为平行四边形;
为顶点的四边形为平行四边形;
(3)点![]() 在
在![]() 边上运动的过程中,以
边上运动的过程中,以![]() 为顶点的四边形能否构成菱形?试说明理由.
为顶点的四边形能否构成菱形?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生对待学习的态度一直是教育工作者关注的问题之一.为此,某区教委对该区部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:

(1)此次抽样调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上![]() ,
,![]() 两点对应的数分别为
两点对应的数分别为![]() 和
和![]() ,点
,点![]() 和点
和点![]() 同时从原点出发,点
同时从原点出发,点![]() 以每秒
以每秒![]() 个单位长度的速度沿数轴正方向运动,点
个单位长度的速度沿数轴正方向运动,点![]() 以每秒
以每秒![]() 个单位长度的速度先沿数轴负方向运动,到达点
个单位长度的速度先沿数轴负方向运动,到达点![]() 后再沿数轴正方向运动,当点
后再沿数轴正方向运动,当点![]() 到达点
到达点![]() 后,两个点同时结束运动.设运动时间为
后,两个点同时结束运动.设运动时间为![]() 秒.
秒.

(1)当![]() 时,求线段
时,求线段![]() 的长度;
的长度;
(2)通过计算说明,当![]() 在不同范围内取值时,线段
在不同范围内取值时,线段![]() 的长度如何用含
的长度如何用含![]() 的式子表示?
的式子表示?
(3)当点![]() 是
是![]() 的中点时直接写出
的中点时直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
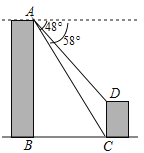
【题目】如图,甲、乙两座建筑物的水平距离BC为78m,从甲的顶部A处测得乙的顶部D处的俯角为48°,测得底部C处的俯角为58°,求乙建筑物的高度CD.(结果取整数,参考数据:tan58°≈1.60,tan48°≈1.11).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(感知)如图①在等边△ABC和等边△ADE中,连接BD,CE,易证:△ABD≌△ACE;
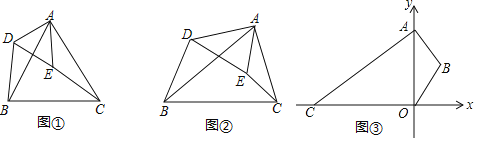
(探究)如图②△ABC与△ADE中,∠BAC=∠DAE,∠ABC=∠ADE,求证:△ABD∽△ACE;
(应用)如图③,点A的坐标为(0,6),AB=BO,∠ABO=120°,点C在x轴上运动,在坐标平面内作点D,使AD=CD,∠ADC=120°,连结OD,则OD的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P和⊙C,给出如下定义:如果⊙C的半径为r,⊙C外一点P到⊙C的切线长小于或等于2r,那么点P叫做⊙C的“离心点”.
(1)当⊙O的半径为1时,
①在点P1(![]() ,
, ![]() ),P2(0,-2),P3(
),P2(0,-2),P3(![]() ,0)中,⊙O的“离心点”是 ;
,0)中,⊙O的“离心点”是 ;
②点P(m,n)在直线![]() 上,且点P是⊙O的“离心点”,求点P横坐标m的取值范围;
上,且点P是⊙O的“离心点”,求点P横坐标m的取值范围;
(2)⊙C的圆心C在y轴上,半径为2,直线![]() 与x轴、y轴分别交于点A,B. 如果线段AB上的所有点都是⊙C的“离心点”,请直接写出圆心C纵坐标的取值范围.
与x轴、y轴分别交于点A,B. 如果线段AB上的所有点都是⊙C的“离心点”,请直接写出圆心C纵坐标的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,李老师和同学们做一个游戏:他在三张硬纸片上分别写出一个代数式,背面分别标上序号①、②、③,摆成如图所示的一个等式,然后翻开纸片②是4x2+5x+6,翻开纸片③是3x2﹣x﹣2.
![]()
解答下列问题
(1)求纸片①上的代数式;
(2)若x是方程2x=﹣x﹣9的解,求纸片①上代数式的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com