
【题目】(感知)如图①在等边△ABC和等边△ADE中,连接BD,CE,易证:△ABD≌△ACE;
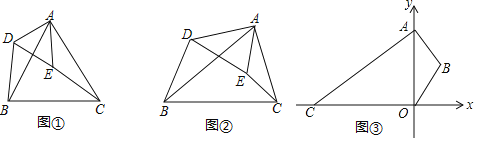
(探究)如图②△ABC与△ADE中,∠BAC=∠DAE,∠ABC=∠ADE,求证:△ABD∽△ACE;
(应用)如图③,点A的坐标为(0,6),AB=BO,∠ABO=120°,点C在x轴上运动,在坐标平面内作点D,使AD=CD,∠ADC=120°,连结OD,则OD的最小值为 .
【答案】探究:见解析;应用:![]() .
.
【解析】
探究:由△DAE∽△BAC,推出![]() ,可得
,可得![]() ,由此即可解决问题;
,由此即可解决问题;
应用:当点D在AC的下方时,先判定△ABO∽△ADC,得出![]() ,再根据∠BAD=∠OAC,得出△ACO∽△ADB,进而得到∠ABD=∠AOC=90°,得到当OD⊥BE时,OD最小,最后过O作OF⊥BD于F,根据∠OBF=30°,求得OF=
,再根据∠BAD=∠OAC,得出△ACO∽△ADB,进而得到∠ABD=∠AOC=90°,得到当OD⊥BE时,OD最小,最后过O作OF⊥BD于F,根据∠OBF=30°,求得OF=![]() OB=
OB=![]() ,即OD最小值为
,即OD最小值为![]() ;当点D在AC的上方时,作B关于y轴的对称点B',则同理可得OD最小值为
;当点D在AC的上方时,作B关于y轴的对称点B',则同理可得OD最小值为![]() .
.
解:探究:如图②中,
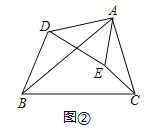
∵∠BAC=∠DAE,∠ABC=∠ADE,
∴△DAE∽△BAC,∠DAB=∠EAC,
∴![]() ,
,
∴![]() ,
,
∴△ABD∽△ACE;
应用:①当点D在AC的下方时,如图③1中,
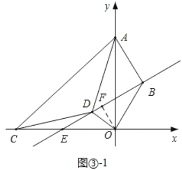
作直线BD,由∠DAC=∠DCA=∠BAO=∠BOA=30°,可得△ABO∽△ADC,
∴![]() ,即
,即![]() ,
,
又∵∠BAD=∠OAC,
∴△ACO∽△ADB,
∴∠ABD=∠AOC=90°,
∵当OD⊥BE时,OD最小,
过O作OF⊥BD于F,则△BOF为直角三角形,
∵A点的坐标是(0,6),AB=BO,∠ABO=120°,
∴易得OB=2![]() ,
,
∵∠ABO=120°,∠ABD=90°,
∴∠OBF=30°,
∴OF=![]() OB=
OB=![]() ,
,
![]() ;
;
当点D在AC的上方时,如图③2中,
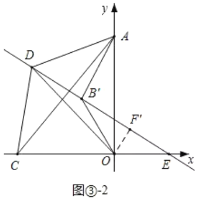
作B关于y轴的对称点B',作直线DB',则同理可得:△ACO∽△ADB',
∴∠AB'D=∠AOC=90°,
∴当OD⊥B'E时,OD最小,
过O作OF'⊥B'D于F',则△B'OF'为直角三角形,
∵A点的坐标是(0,6),AB'=B'O,∠AB'O=120°,
∴易得OB'=2![]() ,
,
∵∠AB'O=120°,∠AB'D=90°,
∴∠OB'F'=30°,
∴OF'=![]() OB'=
OB'=![]() ,
,
即OD最小值为![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】一条高铁线A,B,C三个车站的位置如图所示.已知B,C两站之间相距530千米.高铁列车从B站出发,向C站方向匀速行驶,经过13分钟距A站165千米;经过80分钟距A站500千米.
![]()
(1)求高铁列车的速度和AB两站之间的距离.(2)如果高铁列车从A站出发,开出多久可以到达C站?
查看答案和解析>>
科目:初中数学 来源: 题型:
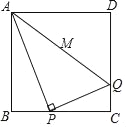
【题目】正方形ABCD的边长为4,P为BC边上的动点,连接AP,作PQ⊥PA交CD边于点Q.当点P从B运动到C时,线段AQ的中点M所经过的路径长( )
A. 2 B. 1 C. 4 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 是线段
是线段![]() 上任一点,
上任一点,![]() ,
,![]() 两点分别从
两点分别从![]() 同时向
同时向![]() 点运动,且
点运动,且![]() 点的运动速度为
点的运动速度为![]() ,
,![]() 点的运动速度为
点的运动速度为![]() ,运动的时间为
,运动的时间为![]() .
.
(1)若![]() ,
,
①运动![]() 后,求
后,求![]() 的长;
的长;
②当![]() 在线段
在线段![]() 上运动时,试说明
上运动时,试说明![]() ;
;
(2)如果![]() 时,
时,![]() ,试探索
,试探索![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①![]() 必是负数;②绝对值最小的数是0;③在数轴上,原点两旁的两个点表示的数必互为相反数;④在数轴上,左边的点比右边的点所表示的数大,其中正确的有( )
必是负数;②绝对值最小的数是0;③在数轴上,原点两旁的两个点表示的数必互为相反数;④在数轴上,左边的点比右边的点所表示的数大,其中正确的有( )
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,AB=4, ![]() O是以AB为直径的圆,以B为圆心,1为半径画弧与
O是以AB为直径的圆,以B为圆心,1为半径画弧与![]() O交于点C,连接AC.请按下列要求回答问题:
O交于点C,连接AC.请按下列要求回答问题:
①sin![]() A等于____________;
A等于____________;
②在线段AB上取一点E,当BE=______________时,连接CE,使线段CE与图中弦(不含直径)所夹角的正弦值等于![]() ;
;
(2)完成操作:仅用无刻度的直尺和圆规作一个直角三角形ABC,使![]() A的正弦值
A的正弦值
等于![]() .(保留作图痕迹,不必说明作法和理由)
.(保留作图痕迹,不必说明作法和理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店第一次购进相同铅笔1000支,第二次又购进同种铅笔,购进数量是第一次的![]() ,这次每支铅笔的进价比第一次进价高0.2元,第二次购进铅笔比第一次少花300元.
,这次每支铅笔的进价比第一次进价高0.2元,第二次购进铅笔比第一次少花300元.
(1)求第一次每支铅笔的进价是多少元?
(2)第一次购进铅笔在第一次进价的基础上加价50%出售;第二次购进的铅笔以每支1.5元的价格出售,出售一部分后又在每支1.5元的基础上打八折出售;两次购进的铅笔全部销售完毕后总获利为560元,问第二次购进的铅笔出售多少支后打八折出售?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com