
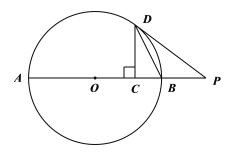
【题目】如图,点D在⊙O上,过点D的切线交直径AB的延长线于点P,DC⊥AB于点C.
(1)求证:DB平分∠PDC;
(2)如果DC = 6,![]() ,求BC的长.
,求BC的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连结OD,如图,利用切线性质得∠ODB+∠PDB=90°,由CD⊥OB得∠CDB+∠DBC=90°,加上∠ODB=∠OBD,于是得到∠CDB=∠PDB,即DB平分∠PDC;
(2)作BE⊥PD,如图,根据角平分线的性质定理得到BC=BE,在Rt△PDC中,利用三角函数的定义计算PC=8,则利用勾股定理可计算出PD=10,设BC=x,则BE=x,PB=8-x,通过证明Rt△PBE∽Rt△PDC,利用相似比得到x:6=(8-x):10,然后根据比例性质求出x即可.
(1)证明:如图,连接OD.
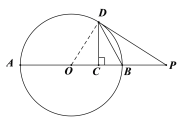
∵ DP是⊙O的切线,
∴ OD⊥DP,
∴ ![]() ,
,
∴ ![]() ,
,
又 ∵DC⊥OB,
∴ ![]() ,
,
∴![]() ,
,
∵OD=OB,
∴![]() ,
,
∴![]() ,
,
∴DB平分∠PDC;
(2)如图,过点B作BE⊥DP于点E.
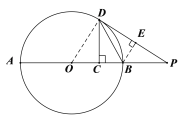
∵![]() ,BC⊥DC,
,BC⊥DC,
∴BC=BE,
∵DC=6,![]() ,
,
∴DP=10,PC=8,
设CB = x,则BE = x,BP = 8 – x,
∵ △PEB∽△PCD,
∴ ![]() ,
,
∴x=3,
∴ ![]() 的长为3.
的长为3.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
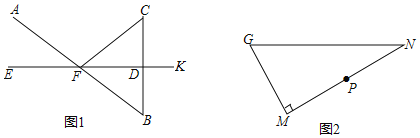
【题目】(1)如图1,已知EK垂直平分BC,垂足为D,AB与EK相交于点F,连接CF.求证:∠AFE=∠CFD.
(2)如图2,在Rt△GMN中,∠M=90°,P为MN的中点.
①用直尺和圆规在GN边上求作点Q,使得∠GQM=∠PQN(保留作图痕迹,不要求写作法);
②在①的条件下,如果∠G=60°,那么Q是GN的中点吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月23日是第二十四个“世界读书日“.某校组织读书征文比赛活动,评选出一、二、三等奖若干名,并绘成如图所示的条形统计图和扇形统计图(不完整),请你根据图中信息解答下列问题:
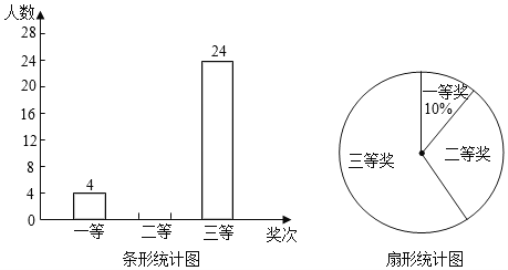
(1)求本次比赛获奖的总人数,并补全条形统计图;
(2)求扇形统计图中“二等奖”所对应扇形的圆心角度数;
(3)学校从甲、乙、丙、丁4位一等奖获得者中随机抽取2人参加“世界读书日”宣传活动,请用列表法或画树状图的方法,求出恰好抽到甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
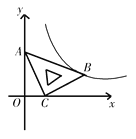
【题目】在平面直角坐标系xOy中,将一块含有45°角的直角三角板如图放置,直角顶点C的坐标为(1,0),AB=![]() ,点A在y轴上,反比例函数经过点B,求反比例函数解析式______.
,点A在y轴上,反比例函数经过点B,求反比例函数解析式______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角![]() 中,延长
中,延长![]() 到点
到点![]() ,点
,点![]() 是
是![]() 边上的一个动点,过点
边上的一个动点,过点![]() 作直线
作直线![]() ,
,![]() 分别交
分别交![]() 、
、![]() 的平分线于
的平分线于![]() ,
,![]() 两点,连接
两点,连接![]() 、
、![]() .在下列结论中.①
.在下列结论中.①![]() ;②
;②![]() ;③若
;③若![]() ,
,![]() ,则
,则![]() 的长为6;④当
的长为6;④当![]() 时,四边形
时,四边形![]() 是矩形.其中正确的是( )
是矩形.其中正确的是( )
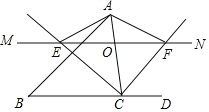
A. ①④B. ①②C. ①②③D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
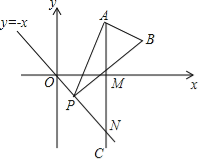
【题目】如图,已知点A是第一象限内横坐标为![]() 的一个定点,AC⊥x轴于点M,交直线y=-x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是 .
的一个定点,AC⊥x轴于点M,交直线y=-x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
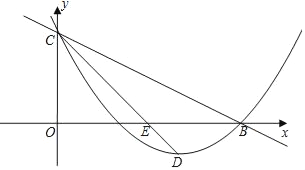
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2﹣2x+c与直线y=﹣![]() x+3分别交于x轴、y轴上的B、C两点,抛物线的顶点为点D,联结CD交x轴于点E.
x+3分别交于x轴、y轴上的B、C两点,抛物线的顶点为点D,联结CD交x轴于点E.
(1)求抛物线的解析式以及点D的坐标;
(2)求tan∠BCD;
(3)点P在直线BC上,若∠PEB=∠BCD,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把有一条边是另一条边的2倍的梯形叫做“倍边梯形”,在⊙O中,直径AB=2,PQ是弦,若四边形ABPQ是“倍边梯形”,那么PQ的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我国新型冠状病毒防控形势好转的态势下,各行各业复工复产所需的“消杀防护”设备成为急需物品.某医药超市库存的甲,乙两种型号“消杀防护”套装共![]() 套全部售完,售后统计甲型号套装每套的利润为
套全部售完,售后统计甲型号套装每套的利润为![]() 元,乙型号套装每套的利润为
元,乙型号套装每套的利润为![]() 元,两种型号“消杀防护"套装售完后的总利润为
元,两种型号“消杀防护"套装售完后的总利润为![]() 元
元
![]() 请计算本次销售中甲、乙两种型号“消杀防护”套装各销售了多少套.
请计算本次销售中甲、乙两种型号“消杀防护”套装各销售了多少套.
![]() 由于企业迫切需求,该医药超市决定再次购进
由于企业迫切需求,该医药超市决定再次购进![]() 套甲、乙两种型号的“消杀防护”套装,商场规定甲型号套装的采购数量不得超过乙型号的
套甲、乙两种型号的“消杀防护”套装,商场规定甲型号套装的采购数量不得超过乙型号的![]() 倍,请你通过计算说明如何采购才能让第二次销售获得最大利润.
倍,请你通过计算说明如何采购才能让第二次销售获得最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com