
【题目】如图,抛物线![]() 与x轴交于点A,B,若点B的坐标为
与x轴交于点A,B,若点B的坐标为![]() .
.
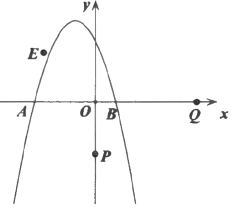
(1)求抛物线的解析式及顶点坐标;
(2)若![]() 是
是![]() 轴上一点,
轴上一点,![]() ,将点Q绕着点P逆时针方向旋转90得到点E.
,将点Q绕着点P逆时针方向旋转90得到点E.
①用含t的式子表示点![]() 的坐标;
的坐标;
②当点E恰好在该抛物线上时,求t的值.
【答案】(1) y=﹣x2﹣2x+3,顶点坐标为(﹣1,4);(2) ①E的坐标为(t,5+t);②t=﹣2
【解析】
(1)把点B的坐标代入二次函数解析式,求出b,利用配方法求出抛物线的顶点坐标;
(2)①作EH⊥y轴于H,证明△EPH≌△PQO,关键全等三角形的性质得到PH=OQ=5,EH=OP=t,得到点E的坐标;
②把点E的坐标代入二次函数解析式,计算得到答案.
解:(1)∵抛物线y=﹣x2+bx+3与x轴交于点B,点B的坐标为(1,0).
∴﹣12+b+3=0,
解得,b=﹣2,
抛物线的解析式为:y=﹣x2﹣2x+3,
y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴抛物线的顶点坐标为(﹣1,4);
(2)①作EH⊥y轴于H,
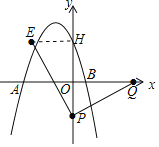
由旋转的性质可知,PE=PQ,∠EPQ=90°,
∴∠EPH+∠HPQ=90°,
∵∠POQ=90°,
∴∠OPQ+∠OQP=90°,
∴∠EPH=∠PQO,
在△EPH和△PQO中,
 ,
,
∴△EPH≌△PQO(AAS),
∴PH=OQ=5,EH=OP=t,
∴OH=PH﹣OP=5+t,
则点E的坐标为(t,5+t);
②当点E恰好在该抛物线上时,﹣t2﹣2t+3=5+t,
解得,t1=﹣2,t2=﹣1
∵t<﹣1,
∴t=﹣2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
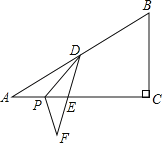
【题目】如图,在Rt△ABC中,∠C=90°,BC=2,∠A=30°,点D是AB的中点,P是AC边上一动点,连接DP,将△DPA沿着DP折叠,A点落到F处,DF与AC交于点E,当△DPF的一边与BC平行时,线段DE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
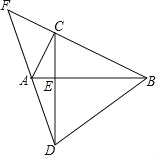
【题目】如图,Rt△ABC中,∠ACB=90°,CD⊥AB于E,CD=AB,DA、BC延长线交于F.
(1)若AC=12,∠ABC=30°,求DE的长;
(2)若BC=2AC,求证:DA=![]() FC.
FC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线ABy=kx﹣1分别交x轴、y轴于点A、B,直线CDy=x+2分别交x轴、y轴于点D、C,且直线AB、CD交于点E,E的横坐标为﹣6.
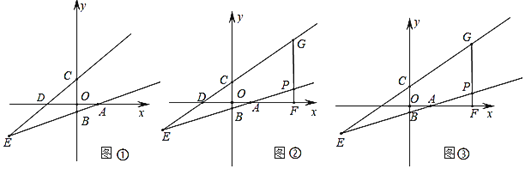
(1)如图①,求直线AB的解析式;
(2)如图②,点P为直线BA第一象限上一点,过P作y轴的平行线交直线CD于G,交x轴于F,在线段PG取点N,在线段AF上取点Q,使GN=QF,在DG上取点M,连接MN、QN,若∠GMN=∠QNF,求![]() 的值;
的值;
(3)在(2)的条件下,点E关于x轴对称点为T,连接MP、TQ,若MP∥TQ,且GN:NP=4:3,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
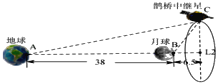
【题目】2019年1月3日,嫦娥四号探测器自主着落在月球背面,实现人类探测器首次月背软着陆.当时,中国已提前发射的“鹊桥”中继星正在地球、月球延长线上的L2点(第二拉格朗日点)附近,沿L2点的动态平衡轨道飞行,为嫦娥四号着陆器和月球车提供地球、月球中继通信支持,保障嫦娥四号任务的完成与实施.如图,已知月球到地球的平均距离约为38万公里,L2点到月球的平均距离约为6.5万公里.某刻,测得线段CL2与AL2垂直,∠CBL2=56°,则下列计算鹊桥中继星到地球的距离AC方法正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的顶点M是直线
的顶点M是直线![]() 和直线y=x+m的交点.
和直线y=x+m的交点.
(1)若直线y=x+m过点D(0,-3),求M点的坐标及二次函数![]() 的解析式;
的解析式;
(2)试证明无论m取任何值,二次函数![]() 的图象与直线y=x+m总有两个不同的交点;
的图象与直线y=x+m总有两个不同的交点;
(3)在(1)的条件下,若二次函数![]() 的图象与y轴交于点C,与x的右交点为A,试在直线
的图象与y轴交于点C,与x的右交点为A,试在直线![]() 上求异于M的点P,使P在△CMA的外接圆上.
上求异于M的点P,使P在△CMA的外接圆上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,∠C=30°,以边上AC上一点O为圆心,OA为半径作⊙O,⊙O恰好经过边BC的中点D,并与边AC相交于另一点F.

(1)求证:BD是⊙O的切线.
(2)若AB=![]() ,E是半圆
,E是半圆![]() 上一动点,连接AE,AD,DE.
上一动点,连接AE,AD,DE.
填空:
①当![]() 的长度是____________时,四边形ABDE是菱形;
的长度是____________时,四边形ABDE是菱形;
②当![]() 的长度是____________时,△ADE是直角三角形.
的长度是____________时,△ADE是直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中考将近,同学们需要花更多的时间来进行自我反思和总结,消化白天的学习内容,提高学习效率.因此,每个班都在积极地进行自我调整.我校![]() 班和
班和![]() 班的同学也积极响应号召,调查了本班的自习情况以供老师参考.
班的同学也积极响应号召,调查了本班的自习情况以供老师参考.
![]() 班同学在班级抽样调查中,调查了十名同学的学习情况,将这十名同学在一周内每天用于自主复习的总时间四舍五入后,分别记录如下:(单位:分)
班同学在班级抽样调查中,调查了十名同学的学习情况,将这十名同学在一周内每天用于自主复习的总时间四舍五入后,分别记录如下:(单位:分)![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 班的同学采取的普查方式,让每位同学自己写出平均每天的自主复习时间,将数据收集整理后得到以下数据.
班的同学采取的普查方式,让每位同学自己写出平均每天的自主复习时间,将数据收集整理后得到以下数据.
平均数 | 中位数 | 众数 | 极差 | 方差 |
|
|
|
|
|
![]() 班的同学还将自主复习时间分为四大类:第一类为时间小于
班的同学还将自主复习时间分为四大类:第一类为时间小于![]() 分钟以下,第二类为时间大于或等于
分钟以下,第二类为时间大于或等于![]() 分钟且小于
分钟且小于![]() 分钟,第三类为时间大于或等于
分钟,第三类为时间大于或等于![]() 分钟且小于
分钟且小于![]() 分钟,第四类为时间大于或等于
分钟,第四类为时间大于或等于![]() 分钟,并得到如下的扇形图.
分钟,并得到如下的扇形图.

(1)在扇形图中,第一类所对的圆心角度数 .
(2)写出![]() 班被调查同学的以下特征数.
班被调查同学的以下特征数.
平均数 | 中位数 | 众数 | 极差 | 方差 |
|
|
|
(3)从上面的数据,我们可以得到 班的自主复习情况要好一些,其理由为(至少两条):
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com