
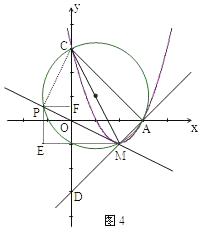
【题目】二次函数![]() 的顶点M是直线
的顶点M是直线![]() 和直线y=x+m的交点.
和直线y=x+m的交点.
(1)若直线y=x+m过点D(0,-3),求M点的坐标及二次函数![]() 的解析式;
的解析式;
(2)试证明无论m取任何值,二次函数![]() 的图象与直线y=x+m总有两个不同的交点;
的图象与直线y=x+m总有两个不同的交点;
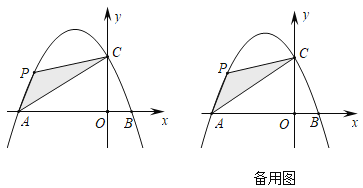
(3)在(1)的条件下,若二次函数![]() 的图象与y轴交于点C,与x的右交点为A,试在直线
的图象与y轴交于点C,与x的右交点为A,试在直线![]() 上求异于M的点P,使P在△CMA的外接圆上.
上求异于M的点P,使P在△CMA的外接圆上.
【答案】(1) M(2,-1),![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() .
.
【解析】
(1)根据题意求出m,解方程组求出M点坐标,根据二次函数的性质求出p、q,得到二次函数的解析式;
(2)根据一元二次方程根的判别式进行判断;
(3)根据二次函数的性质求出点C的坐标、点A的坐标,根据勾股定理求出CM,根据勾股定理的逆定理判断△CMA是直角三角形,根据三角形的外接圆的性质计算.
(1)把D(0,-3)坐标代入直线![]() 中,
中,
得![]() ,从而得直线
,从而得直线![]() ,
,
由M为直线![]() 与直线
与直线![]() 的交点,
的交点,
得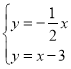 ,
,
解得,![]() ,
,
∴得M点坐标为M(2,-1),
∵M为二次函数![]() 的顶点,
的顶点,
∴其对称轴为![]() ,
,
由对称轴公式:![]() ,
,
得![]() ,
,
∴![]() ;
;
由![]() ,
,
![]() ,
,
解得,![]() .
.
∴二次函数![]() 的解析式为:
的解析式为:![]() ;
;
(2)∵M是直线![]() 和
和![]() 的交点,
的交点,
∴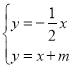 ,
,
解得,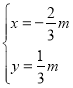 ,
,
∴M点坐标为![]() ,
,
∴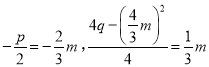 ,
,
解得,![]() ,
,
由![]() ,
,
得![]() ,
,
![]()
![]() ,
,
∴二次函数![]() 的图象与直线
的图象与直线![]() 总有两个不同的交点;
总有两个不同的交点;
(3)由(1)知,二次函数的解析式为:![]() ,
,
当![]() 时,y=3.
时,y=3.
∴点C的坐标为C(0,3),
令y=0,即![]() ,
,
解得![]() ,
,
∴点![]() 的坐标为A(3,0),
的坐标为A(3,0),
由勾股定理,得![]() .
.
∵![]() 点的坐标为M(2,-1),
点的坐标为M(2,-1),
过![]() 点作x轴的垂线,垂足的坐标应为(2,0),
点作x轴的垂线,垂足的坐标应为(2,0),
由勾股定理得,![]() ,
,
过![]() 点作y轴的垂线,垂足的坐标应为(0,-1),
点作y轴的垂线,垂足的坐标应为(0,-1),
由勾股定理,得![]() .
.
∵![]() ,
,
∴△CMA是直角三角形,
CM为斜边,![]() .
.
直线![]() 与△CMA的外接圆的一个交点为M,另一个交点为P,
与△CMA的外接圆的一个交点为M,另一个交点为P,
则![]() .即△CPM为Rt△,
.即△CPM为Rt△,
设P点的横坐标为x,则P(![]() ,
,![]() ).过点P作x轴垂线,
).过点P作x轴垂线,
过点![]() 作y轴垂线,两条垂线交于点E,则E(x,-1).
作y轴垂线,两条垂线交于点E,则E(x,-1).
过P作![]() 轴于点F,则F(0,
轴于点F,则F(0,![]() ).
).
在![]() 中,
中,![]()
![]() .
.
在![]() 中,
中,![]()
![]() .
.
在![]() 中,
中,![]() ,
,
得![]() ,
,
化简整理得![]() ,
,
解得![]() .
.
当![]() 时,y=-1,即为M点的横、纵坐标.
时,y=-1,即为M点的横、纵坐标.
∴P点的横坐标为![]() ,纵坐标为
,纵坐标为![]() ,
,
∴![]() .
.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
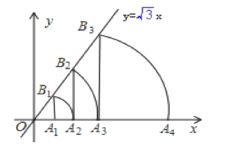
【题目】如图,直线y=![]() x,点A
x,点A![]() 坐标为(1,0),过点A
坐标为(1,0),过点A![]() 作x轴的垂线交直线于点
作x轴的垂线交直线于点![]() ,以原点O为圆心,OB
,以原点O为圆心,OB![]() 长为半径画弧交x轴于点A
长为半径画弧交x轴于点A![]() ;再过点A
;再过点A![]() 作x轴的垂线交直线于点B
作x轴的垂线交直线于点B![]() ,以原点O为圆心,OB
,以原点O为圆心,OB![]() 长为半径画弧交x轴于点A
长为半径画弧交x轴于点A![]() ,…,按此做法进行下去,点A
,…,按此做法进行下去,点A![]() 的坐标为___.
的坐标为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长均为1,点A、B、C、D均在小正方形的顶点上,
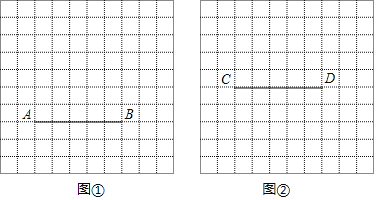
(1)在图①中画出以线段AB为一条边的菱形ABEF,点E、F在小正方形顶点上,且菱形ABEF的面积为20;
(2)在图②中画出以CD为对角线的矩形CGDH,G、H点在小正方形顶点上,点G在CD的下方,且矩形CGDH的面积为10,CG>DG.并直接写出矩形CGDH的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点A,B,若点B的坐标为
与x轴交于点A,B,若点B的坐标为![]() .
.
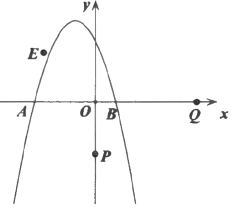
(1)求抛物线的解析式及顶点坐标;
(2)若![]() 是
是![]() 轴上一点,
轴上一点,![]() ,将点Q绕着点P逆时针方向旋转90得到点E.
,将点Q绕着点P逆时针方向旋转90得到点E.
①用含t的式子表示点![]() 的坐标;
的坐标;
②当点E恰好在该抛物线上时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农科所在相同条件下做某种作物种子发芽率的试验,结果如下表所示:
种子个数n | 1000 | 1500 | 2500 | 4000 | 8000 | 15000 | 20000 | 30000 |
发芽种子个数m | 899 | 1365 | 2245 | 3644 | 7272 | 13680 | 18160 | 27300 |
发芽种子频率 | 0.899 | 0.910 | 0.898 | 0.911 | 0.909 | 0.912 | 0.908 | 0.910 |
一般地,![]() 该种作物种子中大约有多少是不能发芽的?
该种作物种子中大约有多少是不能发芽的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的方程(a+1)x2+(2a﹣3)x+a﹣2=0有两个不相等的实根,且关于x的方程![]() 的解为整数,则满足条件的所有整数a的和是_____.
的解为整数,则满足条件的所有整数a的和是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:已知二次函数![]() 经过点
经过点![]() .
.
(1)求该函数的表达式;
(2)如图所示,点![]() 是抛物线上在第二象限内的一个动点,且点
是抛物线上在第二象限内的一个动点,且点![]() 的横坐标为
的横坐标为![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
①求![]() 的面积
的面积![]() 关于
关于![]() 的函数关系式;
的函数关系式;
②求![]() 的面积的最大值,并求出此时点
的面积的最大值,并求出此时点![]() 的坐标.
的坐标.
拓展:在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,
,![]() 的坐标为
的坐标为![]() ,若抛物线
,若抛物线![]() 与线段
与线段![]() 有两个不同的交点,请直接写出
有两个不同的交点,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AB=6,BC=8.点P在矩形ABCD的内部,点E在边BC上,满足△PBE∽△DBC,若△APD是等腰三角形,则PE的长为数___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )

A. B.
B.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com