练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某农科所在相同条件下做某种作物种子发芽率的试验，结果如下表所示：

    种子个数n

    1000

    1500

    2500

    4000

    8000

    15000

    20000

    30000

    发芽种子个数m

    899

    1365

    2245

    3644

    7272

    13680

    18160

    27300

    发芽种子频率

    0．899

    0．910

    0．898

    0．911

    0．909

    0．912

    0．908

    0．910

    一般地，该种作物种子中大约有多少是不能发芽的？

    【答案】90kg．

    【解析】

    根据某农科所在相同条件下做某作物种子发芽率的试验表，可得大量重复试验发芽率逐渐稳定在0.910左右，据此求出1000kg种子中大约有多少kg种子是不能发芽的即可．

    随着种子个数的增加，发芽种子的频率越来越稳定．当种子的个数为30000时，发芽种子的频率为0.910，于是可以估计种子的发芽的概率为0.910．

    ∴1000kg种子中可以发芽的有1000×0.910＝910kg，于是不能发芽的种子有1000－910＝90kg．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图1，某校有一块菱形空地ABCD，∠A=60°，AB=40m，现计划在内部修建一个四个顶点分别落在菱形四条边上的矩形鱼池EFGH，其余部分种花草，园林公司修建鱼池，草坪的造价为y（元）与修建面积s（m2）之间的函数关系如图2所示，设AE为x米．

    （1）填空：ED=　 　m，EH=　 　m，（用含x的代数式表示）；

    （提示：在直角三角形中，30°角所对的直角边等于斜边的一半）

    （2）若矩形鱼池EFGH的面积是300m2，求EF的长度；

    （3）EF的长度为多少时，修建的鱼池和草坪的总造价最低，最低造价为多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将矩形ABCD沿BD翻折，点C落在P点处，连接AP．若∠ABP＝26°，则∠APB＝___________

    查看答案和解析>>

    科目：初中数学 来源： 题型：

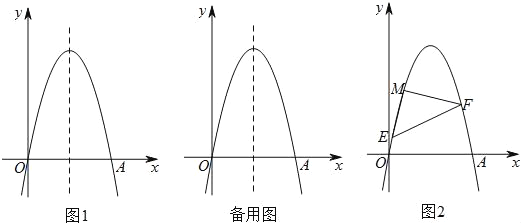
    【题目】如图1，抛物线y=﹣x2+6x与x轴交于O、A两点，点P在抛物线上，过点P的直线y=x+m与抛物线的对称轴交于点Q．

    （1）这条抛物线的对称轴是：直线　 　，直线PQ与x轴所夹锐角的度数是　 　度；

    （2）若S△POQ：S△PAQ=1：2，求此时的点P坐标；

    （3）如图2，点M（1，5）在抛物线上，以点M为直角顶点作Rt△MEF，且E、F均在抛物线上，则所有满足条件的直线EF必然经过定点N，求点N坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】国家主管部门规定：从2008年6月1日起，各商家禁止向消费者免费提供一次性塑料购物袋．为了了解巴中市市民对此规定的看法，对本市年龄在16—65岁之间的居民，进行了400个随机访问抽样调查，并根据每个年龄段的抽查人数和该年龄段对此规定的支持人数绘制了下面的统计图．

    根据上图提供的信息回答下列问题：

    （1）被调查的居民中，人数最多的年龄段是 岁．

    （2）已知被调查的400人中有83%的人对此规定表示支持，请你求出31—40岁年龄段的满意人数，并补全图b．

    （3）比较21—30岁和41—50岁这两个年龄段对此规定的支持率的高低（四舍五入到1%，注：某年龄段的支持率

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个，小李做摸球试验，她将盒子里面的球搅匀后从中随机摸出一个球记下颜色，再把它放回盒子中，不断重复上述过程，下表是试验中的一组统计数据：

    摸球的次数n

    100

    200

    300

    500

    800

    1000

    3000

    摸到白球的次数m

    63

    124

    178

    302

    488

    600

    1800

    摸到白球的频率

    0.63

    0.62

    0.593

    0.604

    0.61

    　 　

    　 　

    （1）完成上表；

    （2）若从盒子中随机摸出一个球，则摸到白球的概率P＝　 　；（结果保留小数点后一位）

    （3）估算这个不透明的盒子里白球有多少个？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列四个图案中，是轴对称图形的是（ ）

    A.B.

    C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，已知在平面直角坐标系中，A（，0），B（4，0），C（0，3），过点C作CD∥x轴，与直线AD交于点D，直线AD与y轴交于点E，连接AC、BD，且tan∠DAB=．

    （1）求直线AD的解析式和线段BD所在直线的解析式．

    （2）如图2，将△CAD沿着直线CD向右平移得△C1A1D1，当C1A1⊥EA1时，在x轴上是否存在点M，使△A1D1M是以A1D1为腰的等腰三角形，若存在，求出△A1D1M的周长；若不存在，请说明理由．

    （3）如图3，延长DB至F，使得BF=DB，点K为线段AD上一动点，连接KF、BK，将△FBK沿BK翻折得△F′BK，请直接写出当DK为何值时，△F′BK与△DBK的重叠部分的面积恰好是△FKD的面积的．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线y=x2﹣6x+9与直线y=x+3交于A，B两点（点A在点B的左侧），抛物线的顶点为C，直线y=x+3与x轴交于点D．

    （Ⅰ）求抛物线的顶点C的坐标及A，B两点的坐标；

    （Ⅱ）将抛物线y=x2﹣6x+9向上平移1个单位长度，再向左平移t（t＞0）个单位长度得到新抛物线，若新抛物线的顶点E在△DAC内，求t的取值范围；

    （Ⅲ）点P（m，n）（﹣3＜m＜1）是抛物线y=x2﹣6x+9上一点，当△PAB的面积是△ABC面积的2倍时，求m，n的值．

    查看答案和解析>>

    同步练习册答案