【题目】下列四个图案中，是轴对称图形的是（ ）
A.
B.
C.
D.
【答案】C
【解析】
根据轴对称图形的概念求解．如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴．
解：A、不是轴对称图形，因为找不到任何这样的一条直线，使它沿这条直线折叠后，直线两旁的部分能够重合，即不满足轴对称图形的定义．不符合题意；
B、不是轴对称图形，因为找不到任何这样的一条直线，使它沿这条直线折叠后，直线两旁的部分能够重合，即不满足轴对称图形的定义．不符合题意；
C、是轴对称图形，符合题意；
D、不是轴对称图形，因为找不到任何这样的一条直线，使它沿这条直线折叠后，直线两旁的部分能够重合，即不满足轴对称图形的定义．不符合题意．
故选：C．
新非凡教辅冲刺100分系列答案科目：初中数学 来源： 题型：
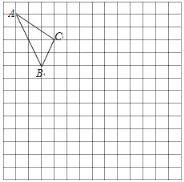
【题目】如图，在正方形网格中，每一个小正方形的边长为1．格点三角形ABC（顶点是网格线交点的三角形）的顶点A，C的坐标分别是（﹣4，6），（﹣1，4）．
（1）请在图中的网格平面内建立平面直角坐标系（直接在图中画出）；
（2）请画出△ABC关于x轴对称的△A1B1C1；
（3）写出点A1、C1的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（提出问题）课间，一位同学拿着方格本遇人便问：“如图所示，在边长为1的小正方形组成的网格中，点A、B、C都是格点，如何证明点A、B、C在同一直线上呢？”
（分析问题）一时间，大家议论开了. 同学甲说：“可以利用代数方法，建立平面直角坐标系，利用函数的知识解决”，同学乙说：“也可以利用几何方法…”同学丙说：“我还有其他的几何证法”……
（解决问题）请你用两种方法解决问题
方法一（用代数方法）：
方法二（用几何方法）：
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】规定：在平面直角坐标系中，将一个图形先关于y轴对称，再向下平移2个单位记为1次“R变换”．如图，已知△ABC的三个顶点均在格点上，其中点B的坐标为(1，2)．
（1）画出△ABC经过1次“R变换”后的图形△A1B1C1；
（2）若△ABC经过3次“R变换”后的图形为△A3B3C3，则顶点A3坐标为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】从南京站开往上海站的一辆和谐号动车，中途只停靠苏州站，甲、乙、丙
名互不相识的旅客同时从南京站上车．
求甲、乙、丙三名旅客在同一个站下车的概率；
求甲、乙、丙三名旅客中至少有一人在苏州站下车的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
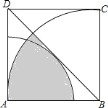
【题目】如图所示，以正方形
的顶点
为圆心的弧恰好与对角线
相切，以顶点
为圆心，正方形的边长为半径的弧，已知正方形的边长为
，则图中阴影部分的面积为（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，在梯形ABCD中，AB∥CD，∠D=90°，AD=CD=2，点E在边AD上（不与点A、D重合），∠CEB=45°，EB与对角线AC相交于点F，设DE=x．
（1）用含x的代数式表示线段CF的长；
（2）如果把△CAE的周长记作C△CAE，△BAF的周长记作C△BAF，设
=y，求y关于x的函数关系式，并写出它的定义域；
（3）当∠ABE的正切值是
时，求AB的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
