
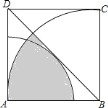
【题目】如图所示,以正方形![]() 的顶点
的顶点![]() 为圆心的弧恰好与对角线
为圆心的弧恰好与对角线![]() 相切,以顶点
相切,以顶点![]() 为圆心,正方形的边长为半径的弧,已知正方形的边长为
为圆心,正方形的边长为半径的弧,已知正方形的边长为![]() ,则图中阴影部分的面积为( )
,则图中阴影部分的面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
连接AC交BD于O,由正方形的性质得出OA=OB=![]() BD,AC⊥BD,∠BAD=90°,AB=AD=2,∠BAO=∠ABF=45°,由勾股定理求出BD,得出OA=OB=
BD,AC⊥BD,∠BAD=90°,AB=AD=2,∠BAO=∠ABF=45°,由勾股定理求出BD,得出OA=OB=![]() ,求出△AOB的面积、扇形AOE的面积、扇形ABF的面积,即可得出图中阴影部分的面积.
,求出△AOB的面积、扇形AOE的面积、扇形ABF的面积,即可得出图中阴影部分的面积.
连接AC交BD于O,如图所示:
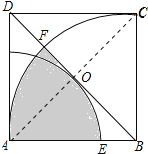
∵四边形ABCD是正方形,
∴OA=OB=![]() BD,AC⊥BD,∠BAD=90°,AB=AD=2,∠BAO=∠ABF=45°,
BD,AC⊥BD,∠BAD=90°,AB=AD=2,∠BAO=∠ABF=45°,
∴BD=![]() =
=![]() ,
,
∴OA=OB=![]() ,
,
∴△AOB的面积=![]() ×
×![]() ×
×![]() =1,
=1,
∵以正方形ABCD的顶点A为圆心的弧恰好与对角线BD相切,AC⊥BD,
∴O为切点,
∵扇形AOE的面积=![]() ,扇形ABF的面积=
,扇形ABF的面积=![]() ,
,
∴图中阴影部分的面积=![]() .
.
故选D.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】如图,点P在长方形OABC的边OA上,连接BP,过点P作BP的垂线,交射线OC于点Q,在点P从点A出发沿AO方向运动到点O的过程中,设AP=x,OQ=y,则下列说法正确的是( )

A.y随x的增大而增大B.y随x的增大而减小
C.随x的增大,y先增大后减小D.随x的增大,y先减小后增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为了调查学生对教学的满意度,随机抽取了部分学生作问卷调查:用“A”表示“很满意“,“B”表示“满意”,“C”表示“比较满意”,“D”表示“不满意”,如图甲、乙是工作人员根据问卷调查统计资料绘制的两幅不完整的统计图,请你根据统计图提供的信息解答以下问题:
(1)本次问卷调查,共调查了多少名学生?
(2)将图甲中“B”部分的图形补充完整;
(3)如果该校有学生1000人,请你估计该校学生对教学感到“不满意”的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=m.若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),则花园面积S的最大值为( )
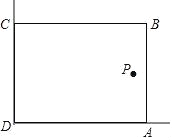
A. 193 B. 194 C. 195 D. 196
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, BD 是△ABC 的角平分线, AE⊥ BD ,垂足为 F ,若∠ABC=35°,∠ C=50°,则∠CDE 的度数为( )
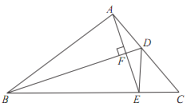
A.35°B.40°C.45°D.50°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,点A、D、B、E在同一直线上,AC=EF,AD=BE,∠A=∠E,
(1)求证:△ABC≌△EDF;
(2)当∠CHD=120°,猜想△HDB的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若△ABC内一点P,满足∠PAB=∠PBC=∠PCA=α,则称点P为△ABC的布洛卡点.通过研究一些特殊三角形中的布洛卡点,得到如下两个结论:
①若∠BAC=90°,则必有∠APC=90°;②若AB=AC,则必有∠APB=∠BPC.
对于这两个结论,下列说法正确的是( )
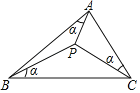
A.①对,②错B.①错,②对C.①,②均错D.①,②均对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com