练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

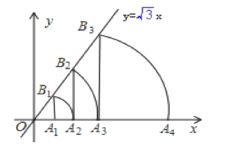
    【题目】如图,直线y=x,点A坐标为(1,0),过点A作x轴的垂线交直线于点,以原点O为圆心,OB 长为半径画弧交x轴于点A;再过点A作x轴的垂线交直线于点B,以原点O为圆心,OB 长为半径画弧交x轴于点A ,…,按此做法进行下去,点A 的坐标为___.

    【答案】(2 ,0).

    【解析】

    根据题意求出B点的坐标，进而找到A点的坐标，逐个解答便可发现规律，进而求得点A的坐标

    已知点A坐标为(1,0),且点B在直线y=x上,可知B1点坐标为(1, )，

    由题意可知OB=OA,故A点坐标为(2,0)，

    同理可求的B点坐标为(2,2)，

    按照这种方法逐个求解便可发现规律,An点坐标为(2 ,0)，

    故点A的坐标为(2 ,0).

    故答案为：(2，0).

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】若直线经过点，直线经过点，且与关于轴对称，则与的交点坐标为（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

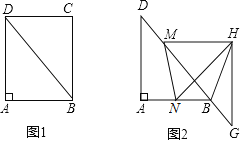
    【题目】如图1在矩形ABCD中，AB＝6，BC＝8，△BCD沿BD的方向匀速平移得到△MGH，速度为1cm/s：同时点N从点B出发，沿BA方向匀速移动，速度为1cm/s，当点N停止移动时，△MGH也停止移动，如图2，设移动时间为t（0＜t＜6），连接MN，HB，HN

    解答下列问题

    （1）当t为何值时，MN∥HG？

    （2）设四边形ADMN面积为y（cm2），求y和t之间的函数关系式；

    （3）是否存在某一时刻t，使S△HBN：S四边形ADMN＝2：3？若存在，求出t值：若不存在，请说明理由；

    （4）是否存在某一时刻t，使MN＝HB？若存在，求出t值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

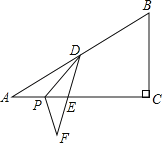
    【题目】如图，在Rt△ABC中，∠C＝90°，BC＝2，∠A＝30°，点D是AB的中点，P是AC边上一动点，连接DP，将△DPA沿着DP折叠，A点落到F处，DF与AC交于点E，当△DPF的一边与BC平行时，线段DE的长为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线y=ax2+bx+c（a≠0）的对称轴是，且经过A（﹣4，0），C（0，2）两点，直线l：y=kx+t（k≠0）经过A，C．

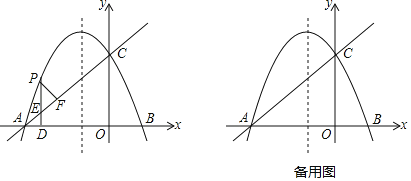
    （1）求抛物线和直线l的解析式；

    （2）点P是直线AC上方的抛物线上一个动点，过点P作PD⊥x轴于点D，交AC于点E，过点P作PF⊥AC，垂足为F，当△PEF≌△AED时，求出点P的坐标；

    （3）在抛物线的对称轴上是否存在点Q，使△ACQ为等腰三角形？若存在，直接写出所有满足条件的Q点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】风电已成为我国继煤电、水电之后的第三大电源，风电机组主要由塔杆和叶片组成（如图1），图2是从图1引出的平面图．假设你站在A处测得塔杆顶端C的仰角是55°，沿HA方向水平前进43米到达山底G处，在山顶B处发现正好一叶片到达最高位置，此时测得叶片的顶端D（D、C、H在同一直线上）的仰角是45°．已知叶片的长度为35米（塔杆与叶片连接处的长度忽略不计），山高BG为10米，BG⊥HG，CH⊥AH，求塔杆CH的高．（参考数据：tan55°≈1.4，tan35°≈0.7，sin55°≈0.8，sin35°≈0.6）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】中华文化历史悠久，包罗万象．某校为了加强学生对中华传统文化的认识和理解，营造校园文化氛围，举办了“弘扬中华传统文化，做新时代的中学生”的知识竞赛．以下是从七年、八年两个年级随机抽取20名同学的测试成绩进行调查分析，成绩如下：

    （1）根据上面的数据，将下列表格补充完整，整理、描述数据：

    50≤x≤59

    60≤x≤69

    70≤x≤79

    80≤x≤89

    90≤x≤100

    七年

    1

    2

    6

    八年

    0

    1

    10

    1

    8

    （说明：成绩90分及以上为优秀，60分以下为不合格）分析数据：

    年级

    平均数

    中位数

    众数

    七年

    84

    88.5

    八年

    84.2

    74

    （2）为调动学生学习传统文化的积极性，七年级根据学生的成绩制定了奖励标准，凡达到或超过这个标准的学生将获得奖励．如果想让一半左右的学生能获奖，应根据　 　来确定奖励标准比较合适．（填“平均数”、“众数”或“中位数”）；

    （3）若八年级有800名学生，试估计八年级学生成绩优秀的人数；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，Rt△ABC中，∠ACB＝90°，CD⊥AB于E，CD＝AB，DA、BC延长线交于F．

    （1）若AC＝12，∠ABC＝30°，求DE的长；

    （2）若BC＝2AC，求证：DA＝FC．

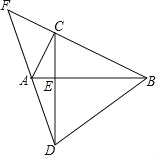
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】二次函数的顶点M是直线和直线y＝x＋m的交点．

    (1)若直线y＝x＋m过点D(0，－3)，求M点的坐标及二次函数的解析式；

    (2)试证明无论m取任何值，二次函数的图象与直线y＝x＋m总有两个不同的交点；

    (3)在(1)的条件下，若二次函数的图象与y轴交于点C，与x的右交点为A，试在直线上求异于M的点P，使P在△CMA的外接圆上．

    查看答案和解析>>

    同步练习册答案