
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴是![]() ,且经过A(﹣4,0),C(0,2)两点,直线l:y=kx+t(k≠0)经过A,C.
,且经过A(﹣4,0),C(0,2)两点,直线l:y=kx+t(k≠0)经过A,C.
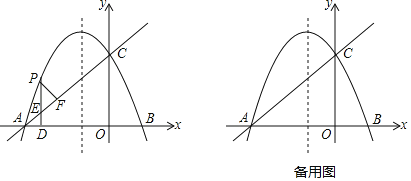
(1)求抛物线和直线l的解析式;
(2)点P是直线AC上方的抛物线上一个动点,过点P作PD⊥x轴于点D,交AC于点E,过点P作PF⊥AC,垂足为F,当△PEF≌△AED时,求出点P的坐标;
(3)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,直接写出所有满足条件的Q点的坐标;若不存在,请说明理由.
【答案】(1)![]() ,
,![]() ;(2)
;(2)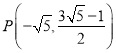 ;(3)存在,Q的坐标为:
;(3)存在,Q的坐标为: 或
或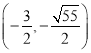
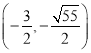 或
或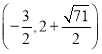 或
或 或
或![]() .
.
【解析】
(1)把点A、C的坐标和对称轴表达式代入二次函数表达式,即可求解;
(2)PE![]() n2
n2![]() n+2
n+2![]() n﹣2,DE
n﹣2,DE![]() n+2,sin∠EAD=sin∠CAO,
n+2,sin∠EAD=sin∠CAO,![]() ,则AE
,则AE![]() DE
DE![]() (
(![]() n+2),当△PEF≌△AED时,PE=AE,
n+2),当△PEF≌△AED时,PE=AE,![]() n2﹣2n
n2﹣2n![]() (
(![]() n+2),即可求解;
n+2),即可求解;
(3)等腰三角形分A为顶角顶点、以C为顶角顶点、点Q为顶角顶点,三种情况分别求解即可.
(1)把点A、C的坐标和对称轴表达式代入二次函数表达式得: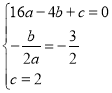 ,解得:
,解得: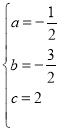 ,故抛物线的表达式为:y
,故抛物线的表达式为:y![]() x2
x2![]() x+2;
x+2;
同理把点A、C坐标代入直线l表达式并解得:y![]() x+2;
x+2;
(2)设P点坐标为(n,![]() n2
n2![]() n+2),∴E点坐标为(n,
n+2),∴E点坐标为(n,![]() n+2),∴PE
n+2),∴PE![]() n2
n2![]() n+2
n+2![]() n﹣2,DE
n﹣2,DE![]() n+2.
n+2.
∵A(﹣4,0),C(0,2),OA=4,OC=2,AC=2![]() .
.
∵PD⊥x轴于点D,∴∠ADE=90°,∴sin∠EAD=sin∠CAO,![]() ,∴AE
,∴AE![]() DE
DE![]() (
(![]() n+2),当△PEF≌△AED时,PE=AE,
n+2),当△PEF≌△AED时,PE=AE,![]() n2﹣2n
n2﹣2n![]() (
(![]() n+2),解得:n=﹣4或
n+2),解得:n=﹣4或![]() (舍去﹣4),∴n=
(舍去﹣4),∴n=![]() ,∴P(
,∴P(![]() ,
,![]() );
);
(3)存在,理由如下:
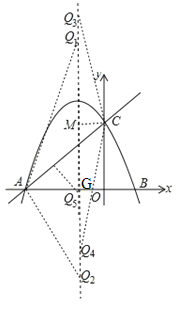
①以A为顶角顶点,AQ=AC,由(2)知AC=2![]() ,若设对称轴与x轴交于点G,则AG
,若设对称轴与x轴交于点G,则AG![]() (﹣4)
(﹣4)![]() ;
;
GQ1=GQ2![]() ,故点Q1、Q2的坐标分别为(
,故点Q1、Q2的坐标分别为(![]() ,
,![]() )、(
)、(![]() ,
,![]() );
);
②以C为顶角顶点,CQ=CA=2![]() ,过点C作x轴的平行线,交抛物线的对称轴于点M,则M(
,过点C作x轴的平行线,交抛物线的对称轴于点M,则M(![]() ,2),则CM
,2),则CM![]() ,MQ3
,MQ3![]() ,Q3G=2
,Q3G=2![]() ,Q4G=﹣2
,Q4G=﹣2![]() ,故Q3、Q4坐标分别为(
,故Q3、Q4坐标分别为(![]() ,2
,2![]() )、(
)、(![]() ,2
,2![]() );
);
③以点Q为顶角顶点时,同理可得点Q5(![]() ,0);
,0);
故点Q的坐标为:(![]() ,
,![]() )或(
)或(![]() ,
,![]() )或(
)或(![]() ,2
,2![]() )或(
)或(![]() ,2
,2![]() )或(
)或(![]() ,0).
,0).


科目:初中数学 来源: 题型:
【题目】某校八年级一班20名女生某次体育测试的成绩统计如下:
成绩(分) | 60 | 70 | 80 | 90 | 100 |
人数(人) | 1 | 5 | x | y | 2 |
(1)如果这20名女生体育成绩的平均分数是82分,求x、y的值;
(2)在(1)的条件下,设20名学生测试成绩的众数是a,中位数是b,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)
(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81,![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=BC,点O是AC的中点,点P是AC上的一个动点(点P不与点A,O,C重合).过点A,点C作直线BP的垂线,垂足分别为点E和点F,连接OE,OF.
(1)如图1,请直接写出线段OE与OF的数量关系;
(2)如图2,当∠ABC=90°时,请判断线段OE与OF之间的数量关系和位置关系,并说明理由
(3)若|CF﹣AE|=2,EF=2![]() ,当△POF为等腰三角形时,请直接写出线段OP的长.
,当△POF为等腰三角形时,请直接写出线段OP的长.
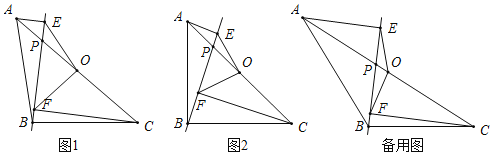
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C是半圆O上一个动点,AB为半圆的直径,D是弧BC的中点,过点D作半圆O的切线DE交AC的延长线于点E.
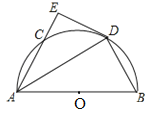
(1)求证:AE⊥DE;
(2)①已知CE=2,DE=4,则AB= ;
②连接OC,DC,当∠BAC= 度时,四边形OBDC为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x,点A
x,点A![]() 坐标为(1,0),过点A
坐标为(1,0),过点A![]() 作x轴的垂线交直线于点
作x轴的垂线交直线于点![]() ,以原点O为圆心,OB
,以原点O为圆心,OB![]() 长为半径画弧交x轴于点A
长为半径画弧交x轴于点A![]() ;再过点A
;再过点A![]() 作x轴的垂线交直线于点B
作x轴的垂线交直线于点B![]() ,以原点O为圆心,OB
,以原点O为圆心,OB![]() 长为半径画弧交x轴于点A
长为半径画弧交x轴于点A![]() ,…,按此做法进行下去,点A
,…,按此做法进行下去,点A![]() 的坐标为___.
的坐标为___.
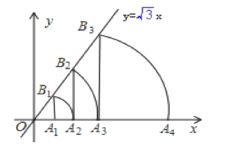
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形OABC的边OC在x轴正半轴上,点B的坐标为(8,4).
(1)请求出菱形的边长;
(2)若反比例函数![]() 经过菱形对角线的交点D,且与边BC交于点E,请求出点E的坐标.
经过菱形对角线的交点D,且与边BC交于点E,请求出点E的坐标.
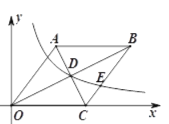
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又剩下一个四边形,称为第二次操作;…依此类推,若第n次操作后,余下的四边形是菱形,则称原平行四边形为n阶准菱形,例如:如图1,ABCD中,若AB=1,BC=2,则ABCD为1阶准菱形.
(1)理解与判断:
邻边长分别为1和3的平行四边形是 阶准菱形;
邻边长分别为3和4的平行四边形是 阶准菱形;
(2)操作、探究与计算:
①已知ABCD的邻边长分别为2,a(a>2),且是3阶准菱形,请画出ABCD及裁剪线的示意图,并在图形下方写出a的值;
②已知ABCD的邻边长分别为a,b(a>b),满足a=7b+r,b=4r,请写出ABCD是几阶准菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农科所在相同条件下做某种作物种子发芽率的试验,结果如下表所示:
种子个数n | 1000 | 1500 | 2500 | 4000 | 8000 | 15000 | 20000 | 30000 |
发芽种子个数m | 899 | 1365 | 2245 | 3644 | 7272 | 13680 | 18160 | 27300 |
发芽种子频率 | 0.899 | 0.910 | 0.898 | 0.911 | 0.909 | 0.912 | 0.908 | 0.910 |
一般地,![]() 该种作物种子中大约有多少是不能发芽的?
该种作物种子中大约有多少是不能发芽的?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com