
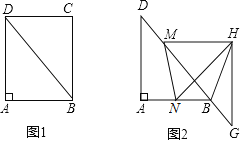
【题目】如图1在矩形ABCD中,AB=6,BC=8,△BCD沿BD的方向匀速平移得到△MGH,速度为1cm/s:同时点N从点B出发,沿BA方向匀速移动,速度为1cm/s,当点N停止移动时,△MGH也停止移动,如图2,设移动时间为t(0<t<6),连接MN,HB,HN
解答下列问题
(1)当t为何值时,MN∥HG?
(2)设四边形ADMN面积为y(cm2),求y和t之间的函数关系式;
(3)是否存在某一时刻t,使S△HBN:S四边形ADMN=2:3?若存在,求出t值:若不存在,请说明理由;
(4)是否存在某一时刻t,使MN=HB?若存在,求出t值;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)t=4,t=6(不合题意舍去);(4)
;(3)t=4,t=6(不合题意舍去);(4)![]()
【解析】
(1)由勾股定理可求BD=10,通过证明△BAD∽△BNM,可得![]() ,即可求t的值;
,即可求t的值;
(2)过点M作ME⊥AB于点E,由相似三角形性质可得ME=![]() (10t),由S四边形ADMN=S△ABD-S△BMN,可得y和t之间的函数关系式;
(10t),由S四边形ADMN=S△ABD-S△BMN,可得y和t之间的函数关系式;
(3)由S△HBN:S四边形ADMN=2:3,可得t2-10t+24=0,即可求t的值;
(4)延长AB交HG于点F,由“HL”可证Rt△MNE≌Rt△HBF,可得BF=EN,即可求t的值.
(1)∵四边形ABCD是矩形
∴AB=CD=6,BC=AD=8,∠A=90°
∴BD=![]() =10
=10
由平移的性质可得:AD∥HG,且NM∥HG
∴MN∥AD
∴△BAD∽△BNM
∴![]()
∴![]()
∴![]() ;
;
(2)如图,过点M作ME⊥AB于点E,
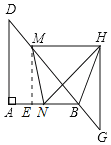
则ME∥AD
∴△BME∽△BDA
∴![]()
∴ME=![]() (10t),
(10t),
∵S四边形ADMN=S△ABD﹣S△BMN,
∴y=24﹣![]() ,(0<t<6)
,(0<t<6)
(3)∵S△HBN:S四边形ADMN=2:3
∴![]()
∴t2﹣10t+24=0
∴t=4,t=6(不合题意舍去)
(4)如图,延长AB交HG于点F,

∵BA∥MH
∴△BFG∽△MHG
∴![]()
∴BF=![]()
∵△BME∽△BDA
∴![]()
∴BE=![]()
∴EN=BE﹣BN=6﹣![]() t,
t,
∵ME=HF,MN=BH
∴Rt△MNE≌Rt△HBF(HL)
∴BF=EN
∴![]() t=6﹣
t=6﹣![]() t,
t,
∴t=![]() .
.


 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]()
![]() 的图象相交于点
的图象相交于点![]() 和
和![]() .
.

(1)求一次函数和反比例函数的解析式;
(2)若定义横、纵坐标均为整数的点叫做好点,则图中阴影部分区域内(不含边界)好点的个数为________;
(3)请根据图象直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
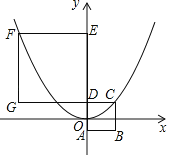
【题目】如图,四边形ABCD、DEFG都是正方形,边长分别为m、n(m<n).坐标原点O为AD的中点,A、D、E在y轴上.若二次函数y=ax2的图象过C、F两点,则![]() =_____.
=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自2016年国庆后,许多高校均投放了使用手机就可随用的共享单车.某运营商为提高其经营的A品牌共享单车的市场占有率,准备对收费作如下调整:一天中,同一个人第一次使用的车费按0.5元收取,每增加一次,当次车费就比上次车费减少0.1元,第6次开始,当次用车免费.具体收费标准如下:
使用次数 | 0 | 1 | 2 | 3 | 4 | 5(含5次以上) |
累计车费 | 0 | 0.5 | 0.9 |
|
| 1.5 |
同时,就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿,得到如下数据:
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 5 | 15 | 10 | 30 | 25 | 15 |
(Ⅰ)写出![]() 的值;
的值;
(Ⅱ)已知该校有5000名师生,且A品牌共享单车投放该校一天的费用为5800元.试估计:收费调整后,此运营商在该校投放A品牌共享单车能否获利? 说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)
(参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81,![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,m,n是一元二次方程x2+4x+3=0的两个实数根,且|m|<|n|,抛物线y=x2+bx+c的图象经过点A(m,0),B(0,n),如图所示.
(1)求这个抛物线的解析式;
(2)设(1)中的抛物线与x轴的另一个交点为抛物线的顶点为D,求出点C,D的坐标,并判断△BCD的形状;
(3)点P是直线BC上的一个动点(点P不与点B和点C重合),过点P作x轴的垂线,交抛物线于点M,点Q在直线BC上,距离点P为![]() 个单位长度,设点P的横坐标为t,△PMQ的面积为S,求出S与t之间的函数关系式.
个单位长度,设点P的横坐标为t,△PMQ的面积为S,求出S与t之间的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
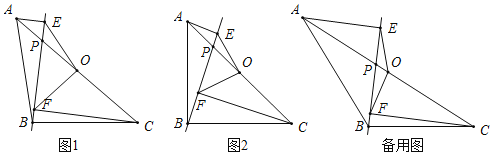
【题目】在△ABC中,AB=BC,点O是AC的中点,点P是AC上的一个动点(点P不与点A,O,C重合).过点A,点C作直线BP的垂线,垂足分别为点E和点F,连接OE,OF.
(1)如图1,请直接写出线段OE与OF的数量关系;
(2)如图2,当∠ABC=90°时,请判断线段OE与OF之间的数量关系和位置关系,并说明理由
(3)若|CF﹣AE|=2,EF=2![]() ,当△POF为等腰三角形时,请直接写出线段OP的长.
,当△POF为等腰三角形时,请直接写出线段OP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
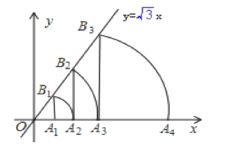
【题目】如图,直线y=![]() x,点A
x,点A![]() 坐标为(1,0),过点A
坐标为(1,0),过点A![]() 作x轴的垂线交直线于点
作x轴的垂线交直线于点![]() ,以原点O为圆心,OB
,以原点O为圆心,OB![]() 长为半径画弧交x轴于点A
长为半径画弧交x轴于点A![]() ;再过点A
;再过点A![]() 作x轴的垂线交直线于点B
作x轴的垂线交直线于点B![]() ,以原点O为圆心,OB
,以原点O为圆心,OB![]() 长为半径画弧交x轴于点A
长为半径画弧交x轴于点A![]() ,…,按此做法进行下去,点A
,…,按此做法进行下去,点A![]() 的坐标为___.
的坐标为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长均为1,点A、B、C、D均在小正方形的顶点上,
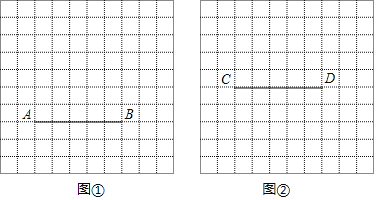
(1)在图①中画出以线段AB为一条边的菱形ABEF,点E、F在小正方形顶点上,且菱形ABEF的面积为20;
(2)在图②中画出以CD为对角线的矩形CGDH,G、H点在小正方形顶点上,点G在CD的下方,且矩形CGDH的面积为10,CG>DG.并直接写出矩形CGDH的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com