
ЁОЬтФПЁПвбжЊЃЌmЃЌnЪЧвЛдЊЖўДЮЗНГЬx2+4x+3=0ЕФСНИіЪЕЪ§ИљЃЌЧв|m|ЃМ|n|ЃЌХзЮяЯпy=x2+bx+cЕФЭМЯѓОЙ§ЕуAЃЈmЃЌ0ЃЉЃЌBЃЈ0ЃЌnЃЉЃЌШчЭМЫљЪОЃЎ
ЃЈ1ЃЉЧѓетИіХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЩшЃЈ1ЃЉжаЕФХзЮяЯпгыxжсЕФСэвЛИіНЛЕуЮЊХзЮяЯпЕФЖЅЕуЮЊDЃЌЧѓГіЕуCЃЌDЕФзјБъЃЌВЂХаЖЯЁїBCDЕФаЮзДЃЛ
ЃЈ3ЃЉЕуPЪЧжБЯпBCЩЯЕФвЛИіЖЏЕуЃЈЕуPВЛгыЕуBКЭЕуCжиКЯЃЉЃЌЙ§ЕуPзїxжсЕФДЙЯпЃЌНЛХзЮяЯпгкЕуMЃЌЕуQдкжБЯпBCЩЯЃЌОрРыЕуPЮЊ![]() ИіЕЅЮЛГЄЖШЃЌЩшЕуPЕФКсзјБъЮЊtЃЌЁїPMQЕФУцЛ§ЮЊSЃЌЧѓГіSгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ
ИіЕЅЮЛГЄЖШЃЌЩшЕуPЕФКсзјБъЮЊtЃЌЁїPMQЕФУцЛ§ЮЊSЃЌЧѓГіSгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ

ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉCЃЈ3ЃЌ0ЃЉЃЌDЃЈ1ЃЌЉ4ЃЉЃЌЁїBCDЪЧжБНЧШ§НЧаЮЃЛЃЈ3ЃЉ
ЃЛЃЈ2ЃЉCЃЈ3ЃЌ0ЃЉЃЌDЃЈ1ЃЌЉ4ЃЉЃЌЁїBCDЪЧжБНЧШ§НЧаЮЃЛЃЈ3ЃЉ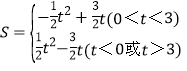
ЁОНтЮіЁП
ЪдЬтЃЈ1ЃЉЯШНтвЛдЊЖўДЮЗНГЬЃЌШЛКѓгУД§ЖЈЯЕЪ§ЗЈЧѓГіХзЮяЯпНтЮіЪНЃЛ
ЃЈ2ЃЉЯШНтЗНГЬЧѓГіХзЮяЯпгыxжсЕФНЛЕуЃЌдйХаЖЯГіЁїBOCКЭЁїBEDЖМЪЧЕШбќжБНЧШ§НЧаЮЃЌДгЖјЕУЕННсТлЃЛ
ЃЈ3ЃЉЯШЧѓГіQF=1ЃЌдйЗжСНжжЧщПіЃЌЕБЕуPдкЕуMЩЯЗНКЭЯТЗНЃЌЗжБ№МЦЫуМДПЩЃЎ
ЪдЬтНтЮіЃКНтЃЈ1ЃЉЁп![]() ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ![]() ЃЌЁпmЃЌnЪЧвЛдЊЖўДЮЗНГЬ
ЃЌЁпmЃЌnЪЧвЛдЊЖўДЮЗНГЬ![]() ЕФСНИіЪЕЪ§ИљЃЌЧв|m|ЃМ|n|ЃЌЁрm=Љ1ЃЌn=Љ3ЃЌЁпХзЮяЯп
ЕФСНИіЪЕЪ§ИљЃЌЧв|m|ЃМ|n|ЃЌЁрm=Љ1ЃЌn=Љ3ЃЌЁпХзЮяЯп![]() ЕФЭМЯѓОЙ§ЕуAЃЈmЃЌ0ЃЉЃЌBЃЈ0ЃЌnЃЉЃЌЁр
ЕФЭМЯѓОЙ§ЕуAЃЈmЃЌ0ЃЉЃЌBЃЈ0ЃЌnЃЉЃЌЁр![]() ЃЌЁр
ЃЌЁр![]() ЃЌЁрХзЮяЯпНтЮіЪНЮЊ
ЃЌЁрХзЮяЯпНтЮіЪНЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉСюy=0ЃЌдђ![]() ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ![]() ЃЌЁрCЃЈ3ЃЌ0ЃЉЃЌЁп
ЃЌЁрCЃЈ3ЃЌ0ЃЉЃЌЁп![]() =
=![]() ЃЌЁрЖЅЕузјБъDЃЈ1ЃЌЉ4ЃЉЃЌЙ§ЕуDзїDEЁЭyжсЃЌЁпOB=OC=3ЃЌЁрBE=DE=1ЃЌЁрЁїBOCКЭЁїBEDЖМЪЧЕШбќжБНЧШ§НЧаЮЃЌЁрЁЯOBC=ЁЯDBE=45ЁуЃЌЁрЁЯCBD=90ЁуЃЌЁрЁїBCDЪЧжБНЧШ§НЧаЮЃЛ
ЃЌЁрЖЅЕузјБъDЃЈ1ЃЌЉ4ЃЉЃЌЙ§ЕуDзїDEЁЭyжсЃЌЁпOB=OC=3ЃЌЁрBE=DE=1ЃЌЁрЁїBOCКЭЁїBEDЖМЪЧЕШбќжБНЧШ§НЧаЮЃЌЁрЁЯOBC=ЁЯDBE=45ЁуЃЌЁрЁЯCBD=90ЁуЃЌЁрЁїBCDЪЧжБНЧШ§НЧаЮЃЛ
ЃЈ3ЃЉШчЭМЃЌЁпBЃЈ0ЃЌЉ3ЃЉЃЌCЃЈ3ЃЌ0ЃЉЃЌЁржБЯпBCНтЮіЪНЮЊy=xЉ3ЃЌЁпЕуPЕФКсзјБъЮЊtЃЌPMЁЭxжсЃЌЁрЕуMЕФКсзјБъЮЊtЃЌЁпЕуPдкжБЯпBCЩЯЃЌЕуMдкХзЮяЯпЩЯЃЌЁрPЃЈtЃЌtЉ3ЃЉЃЌMЃЈtЃЌ![]() ЃЉЃЌЙ§ЕуQзїQFЁЭPMЃЌЁрЁїPQFЪЧЕШбќжБНЧШ§НЧаЮЃЌЁпPQ=
ЃЉЃЌЙ§ЕуQзїQFЁЭPMЃЌЁрЁїPQFЪЧЕШбќжБНЧШ§НЧаЮЃЌЁпPQ=![]() ЃЌЁрQF=1ЃЎ
ЃЌЁрQF=1ЃЎ
ЂйЕБЕуPдкЕуMЩЯЗНЪБЃЌМД0ЃМtЃМ3ЪБЃЌPM=tЉ3ЉЃЈ![]() ЃЉ=
ЃЉ=![]() ЃЌЁрS=
ЃЌЁрS=![]() PMЁСQF=
PMЁСQF=![]() =
=![]() ЃЌЂкШчЭМ3ЃЌЕБЕуPдкЕуMЯТЗНЪБЃЌМДtЃМ0ЛђtЃО3ЪБЃЌPM=
ЃЌЂкШчЭМ3ЃЌЕБЕуPдкЕуMЯТЗНЪБЃЌМДtЃМ0ЛђtЃО3ЪБЃЌPM=![]() ЉЃЈtЉ3ЃЉ=
ЉЃЈtЉ3ЃЉ=![]() ЃЌЁрS=
ЃЌЁрS=![]() PMЁСQF=
PMЁСQF=![]() ЃЈ
ЃЈ![]() ЃЉ=
ЃЉ=![]() ЃЎ
ЃЎ
злЩЯЫљЪіЃЌS=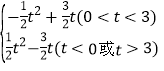 ЃЎ
ЃЎ


 УћЪІН№ЪжжИСьЯЮПЮЪБЯЕСаД№АИ
УћЪІН№ЪжжИСьЯЮПЮЪБЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЋЫОЭЦГіСЫМзЁЂввСНжжаТЦЗвћСЯЃЌЫќУЧЖМгЩAЁЂBЁЂCШ§жжШмвКзщГЩЃЌжЛЪЧМзжжвћСЯУПЦПзАга200ПЫAШмвКЃЌ200ПЫBШмвКЃЌ100ПЫCШмвКЃЛввжжвћСЯУПЦПзАга100ПЫAШмвКЃЌ100ПЫBШмвКЃЌ300ПЫCШмвКЃЌМзЁЂввСНжжвћСЯУПЦПГЩБОМлОљЮЊЦПжаAЁЂBЁЂCШ§жжШмвКЕФГЩБОМлжЎКЭЃЎвбжЊCжжШмвКУПвЛАйПЫЕФГЩБОМлЮЊ1дЊЃЌввжжвћСЯУПЦПЪлМлЮЊ10дЊЃЌРћШѓТЪЮЊ![]() ЃЌМзжжвћСЯУПЦПЕФРћШѓТЪЮЊ20%ЃЌЧѓетСНжжвћСЯЕФЯњЪлРћШѓТЪЮЊ24%ЪБЃЌИУЙЋЫОЯњЪлМзЁЂввСНжжвћСЯЕФЪ§СПжЎБШЪЧ_____ЃЎ
ЃЌМзжжвћСЯУПЦПЕФРћШѓТЪЮЊ20%ЃЌЧѓетСНжжвћСЯЕФЯњЪлРћШѓТЪЮЊ24%ЪБЃЌИУЙЋЫОЯњЪлМзЁЂввСНжжвћСЯЕФЪ§СПжЎБШЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§yЃНx2Ѓ4xЃЋ3.
(1)гУХфЗНЗЈЧѓЦфЭМЯѓЕФЖЅЕуCЕФзјБъЃЌВЂУшЪіИУКЏЪ§ЕФКЏЪ§жЕЫцздБфСПЕФдіМѕЖјБфЛЏЕФЧщПіЃЛ
(2)ЧѓКЏЪ§ЭМЯѓгыxжсЕФНЛЕуAЃЌBЕФзјБъЃЌМАЁїABCЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ14ЗжЃЉШчЭМЃЌвбжЊдкОиаЮABCDжаЃЌAB=aЃЌBC=bЃЌЕуEЪЧЯпЖЮADБпЩЯЕФШЮвтвЛЕуЃЈВЛКЌЖЫЕуAЁЂDЃЉЃЌСЌНсBEЁЂCEЃЎ
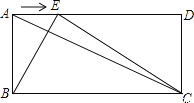
ЃЈ1ЃЉШєa=5ЃЌAC=13ЃЌЧѓbЃЎ
ЃЈ2ЃЉШєa=5ЃЌb=10,ЕБBEЁЭACЪБЃЌЧѓГіДЫЪБAEЕФГЄЃЎ
ЃЈ3ЃЉЩшAE=xЃЌЪдЬНЫїЕуEдкЯпЖЮADЩЯдЫЖЏЙ§ГЬжаЃЌЪЙЕУЁїABEгыЁїBCEЯрЫЦЪБЃЌЧѓaЁЂbгІТњзуЪВУДЬѕМўЃЌВЂЧѓГіДЫЪБxЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯжДњЛЅСЊЭјММЪѕЕФЙуЗКгІгУЃЌДпЩњСЫПьЕнаавЕЕФИпЫйЗЂеЙЃЎИЗбєЪаФГМвПьЕнЙЋЫОЃЌ2017Фъ3дТЗнгы5дТЗнЭъГЩЭЖЕнЕФПьЕнзмМўЪ§ЗжБ№ЮЊ10ЭђМўКЭ12.1ЭђМўЃЎЯжМйЖЈИУЙЋЫОУПдТЭЖЕнЕФПьЕнзмМўЪ§ЕФдіГЄТЪЯрЭЌЃЎ
(1)ЧѓИУПьЕнЙЋЫОЭЖЕнПьЕнзмМўЪ§ЕФдТЦНОљдіГЄТЪЃП
(2) ШчЙћЦНОљУПШЫУПдТзюЖрПЩЭЖЕнПьЕн0.6ЭђМўЃЌФЧУДИУЙЋЫОЯжгаЕФ21УћПьЕнЭЖЕнвЕЮёдБФмЗёЭъГЩ2017Фъ6дТЗнЕФПьЕнЭЖЕнШЮЮёЃПШчЙћВЛФмЃЌЧыЮЪжСЩйашвЊдіМгМИУћвЕЮёдБЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊдкЦНУцжБНЧзјБъЯЕжаЃЌAB СНЕуЕФзјБъЗжБ№ЮЊ A(1,4),B(5,1),PЃЌQ ЗжБ№ЪЧ x жсЃЌy жс ЩЯСНИіЖЏЕуЃЌдђЫФБпаЮ ABPQ ЕФжмГЄзюаЁжЕЮЊЃЈ ЃЉ
A.5B.5 ![]() C.
C.![]()
![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЙигкxЕФвЛдЊЖўДЮЗНГЬx2Љ2x+mЉ1=0гаСНИіЪЕЪ§Иљx1ЃЌx2ЃЎ
ЃЈ1ЃЉЧѓmЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉЕБx12+x22=6x1x2ЪБЃЌЧѓmЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЧыдФЖСЯТСаВФСЯЃК
ЮвУЧПЩвдЭЈЙ§вдЯТЗНЗЈЧѓДњЪ§ЪН![]() ЕФзюаЁжЕЃЎ
ЕФзюаЁжЕЃЎ
![]() ЃЌ
ЃЌ
Ёп![]() Ён0ЃЌ
Ён0ЃЌ
ЁрЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() газюаЁжЕ
газюаЁжЕ![]() ЃЎ
ЃЎ
ЧыИљОнЩЯЪіЗНЗЈЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉ![]() ЃЌдђ
ЃЌдђ![]() ЕФжЕЪЧ______ЃЛ
ЕФжЕЪЧ______ЃЛ
ЃЈ2ЃЉЧѓжЄЃКЮоТлxШЁКЮжЕЃЌДњЪ§ЪН![]() ЕФжЕЖМЪЧе§Ъ§ЃЛ
ЕФжЕЖМЪЧе§Ъ§ЃЛ
ЃЈ3ЃЉШєДњЪ§ЪН![]() ЕФзюаЁжЕЮЊ2ЃЌЧѓkЕФжЕЃЎ
ЕФзюаЁжЕЮЊ2ЃЌЧѓkЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
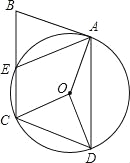
ЁОЬтФПЁПШчЭМЃЌABCDЕФЖЅЕуAЁЂCЁЂDЖМдкЁбOЩЯЃЌABгыЁбOЯрЧагкЕуAЃЌBCгыЁбOНЛгкЕуEЃЌЩшЁЯOCD=ІСЃЌЁЯBAD=ІТЃЎ
ЃЈ1ЃЉЧѓжЄЃКAB=AEЃЛ
ЃЈ2ЃЉЪдЬНОПІСгыІТжЎМфЕФЪ§СПЙиЯЕЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com