练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知在平面直角坐标系中，AB 两点的坐标分别为 A(1,4),B(5,1),P，Q 分别是 x 轴，y 轴 上两个动点，则四边形 ABPQ 的周长最小值为（ ）

    A.5B.5 C.D.

    【答案】D

    【解析】

    作点A关于y轴的对称点A'，点B关于x轴的对称点B'，连接A'B'，交x轴于P，交y轴于Q，连接AQ，BP，则四边形AQPB周长的最小值等于A'B'+AB，利用勾股定理进行计算，即可得到四边形AQPB周长的最小值．

    解：如图所示，作点A关于y轴的对称点A'，点B关于x轴的对称点B'，连接A'B'，交x轴于P，交y轴于Q，连接AQ，BP，则四边形AQPB周长的最小值等于A'B'+AB，


    ∵A（1，4），B（5，1），
    ∴A'（-1，4），B'（5，-1），
    ∴A'B'=，
    ∴四边形AQPB周长的最小值等于，
    故选D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，AD和BE是高，∠ABE=45°，点F是AB的中点，AD与FE，BE分别交于点G、H．∠CBE=∠BAD，有下列结论：①FD=FE；②AH=2CD；③BCAD=AE2；④S△BEC=S△ADF．其中正确的有（　　）

    A. 1个 B. 2个 C. 3个 D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】函数y＝与y＝－kx2＋k(k≠0)在同一坐标系中图象可能是（ ）

    A. B.

    C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AD是BC边上的高，AE是∠BAC的平分线，∠B=40°，∠DAE=15°，求∠C的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，m，n是一元二次方程x2+4x+3=0的两个实数根，且|m|＜|n|，抛物线y=x2+bx+c的图象经过点A（m，0），B（0，n），如图所示．

    （1）求这个抛物线的解析式；

    （2）设（1）中的抛物线与x轴的另一个交点为抛物线的顶点为D，求出点C，D的坐标，并判断△BCD的形状；

    （3）点P是直线BC上的一个动点（点P不与点B和点C重合），过点P作x轴的垂线，交抛物线于点M，点Q在直线BC上，距离点P为个单位长度，设点P的横坐标为t，△PMQ的面积为S，求出S与t之间的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】本学期初，某校为迎接中华人民共和国建国七十周年，开展了以“不忘初心，缅怀革命先烈，奋斗新时代”为主题的读书活动．校德育处对本校八年级学生四月份“阅读该主题相关书籍的读书量”（下面简称：“读书量）进行了随机抽样调查并对所有随机抽取学生的“读书量”（单位：本）进行了统计，如图所示：

    根据以上信息，解答下列问题：

    （1）补全上面两幅统计图，填出本次所抽取学生四月份“读书量”的众数为　 　．

    （2）求本次所抽取学生四月份“读书量”的平均数；

    （3）已知该校八年级有1200名学生，请你估计该校八年级学生中，四月份“读书量”为4本及以上的学生人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题探究

    (1)如图①，在△ABC 中，∠B=30°，E 是 AB 边上的点，过点 E 作 EF⊥BC 于 F，则的值为 .

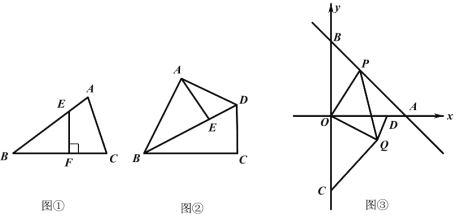
    （2）如图②，在四边形 ABCD 中，AB=BC=6,∠ABC=60°，对角线 BD 平分∠ABC，点E 是对角线 BD 上一点，求 AE+ BE的最小值.

    问题解决

    （3）如图③，在平面直角坐标系中，直线 y -x 4 分别于 x 轴，y 轴交于点 A、B，点 P 为直线 AB 上的动点，以 OP 为边在其下方作等腰 Rt△OPQ 且∠POQ=90°.已知点C（0，-4），点 D（3,0）连接 CQ、DQ,那么DQ CQ是否存在最小值，若存在求出其最小值及此时点 P 的坐标，若不存在请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有一对酷爱运动的年轻夫妇给他们12个月大的婴儿拼排3块分别写有“20”，“08”和“北京”的字块，如果婴儿能够排成“2008北京”或者“北京2008”．则他们就给婴儿奖励，假设婴儿能将字块横着正排，那么这个婴儿能得到奖励的概率是___________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，直角△ABC的三个顶点分别是A（﹣3，1），B（0，3），C（0，1）

    （1）将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△A1B1C1；

    （2）分别连结AB1、BA1后，求四边形AB1A1B的面积．

    查看答案和解析>>

    同步练习册答案