
【题目】问题探究
(1)如图①,在△ABC 中,∠B=30°,E 是 AB 边上的点,过点 E 作 EF⊥BC 于 F,则![]() 的值为 .
的值为 .
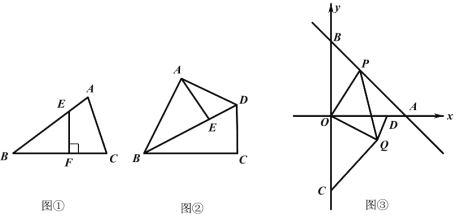
(2)如图②,在四边形 ABCD 中,AB=BC=6,∠ABC=60°,对角线 BD 平分∠ABC,点E 是对角线 BD 上一点,求 AE+ ![]() BE的最小值.
BE的最小值.
问题解决
(3)如图③,在平面直角坐标系中,直线 y -x 4 分别于 x 轴,y 轴交于点 A、B,点 P 为直线 AB 上的动点,以 OP 为边在其下方作等腰 Rt△OPQ 且∠POQ=90°.已知点C(0,-4),点 D(3,0)连接 CQ、DQ,那么DQ ![]() CQ是否存在最小值,若存在求出其最小值及此时点 P 的坐标,若不存在请说明理由.
CQ是否存在最小值,若存在求出其最小值及此时点 P 的坐标,若不存在请说明理由.
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)4.
;(3)4.
【解析】
(1)利用直角三角形中,30°所对的直角边等于斜边的一半求解即可;
(2) 作EF⊥BC于F, 根据直角三角形中,30°所对的直角边等于斜边的一半,得到AE+![]() BE=AE+EF ,再根据勾股定理得到AE+
BE=AE+EF ,再根据勾股定理得到AE+![]() BE的最小值;
BE的最小值;
(3) 作PM⊥y轴于M,QN⊥y轴于N,易证△POM≌△OQN,根据当![]() 、Q、N共线时,
、Q、N共线时,![]() Q+NQ最小求解即可.
Q+NQ最小求解即可.
解;(1) ∵EF⊥BC, ∴∠BFE=90°, ∵∠B=30°, ∴![]() =
=![]() ;
;
(2)作EF⊥BC于F, ∵∠ABC=60°,对角线 BD 平分∠ABC,∴∠DBC=30°, ∴∠EF=![]() BE, ∴AE+
BE, ∴AE+![]() BE=AE+EF, ∴当点A、E、F三点在一条直线时,AE+
BE=AE+EF, ∴当点A、E、F三点在一条直线时,AE+![]() BE 最小,∵∠ABF=60°, ∴∠BAF=30°, ∵AB=6, ∴BF=
BE 最小,∵∠ABF=60°, ∴∠BAF=30°, ∵AB=6, ∴BF=![]() AB=3, ∴AF=
AB=3, ∴AF=![]() , ∴AE+
, ∴AE+![]() BE的最小值为
BE的最小值为![]() .
.
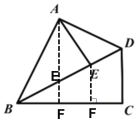
(3) ∵y=-x+4, ∴B(0,4),A(4,0),
作PM⊥y轴于M,QN⊥y轴于N, ∴∠PMO=∠QNO=90°, ∵∠POM+MPO=∠POM+∠QON=90°∴∠MPO=∠QON, ∵PO=QO, ∴△POM≌△OQN,设BM=PM=ON=t,则OM=NQ=CN=4-t, ∴无论P在任何位置△CNQ都为等腰三角形,∠NCQ=45°,则Q点永远在直线AC上,作D点关于直线AC的对称点![]() , ∵D(3,0), ∴
, ∵D(3,0), ∴![]() (4,-1),则DQ+NQ=
(4,-1),则DQ+NQ=![]() Q+NQ, ∴当
Q+NQ, ∴当![]() 、Q、N共线时,
、Q、N共线时,![]() Q+NQ最小,最小值是N
Q+NQ最小,最小值是N![]() =4.
=4.



 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,等边三角形ABC的顶点B与原点O重合,点C在x轴上,点C坐标为(6,0),等边三角形ABC的三边上有三个动点D、E、F(不考虑与A、B、C重合),点D从A向B运动,点E从B向C运动,点F从C向A运动,三点同时运动,到终点结束,且速度均为1cm/s,设运动的时间为ts,解答下列问题:
(1)求证:如图①,不论t如何变化,△DEF始终为等边三角形.
(2)如图②过点E作EQ∥AB,交AC于点Q,设△AEQ的面积为S,求S与t的函数关系式及t为何值时△AEQ的面积最大?求出这个最大值.
(3)在(2)的条件下,当△AEQ的面积最大时,平面内是否存在一点P,使A、D、Q、P构成的四边形是菱形,若存在请直接写出P坐标,若不存在请说明理由?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(14分)如图,已知在矩形ABCD中,AB=a,BC=b,点E是线段AD边上的任意一点(不含端点A、D),连结BE、CE.
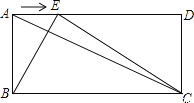
(1)若a=5,AC=13,求b.
(2)若a=5,b=10,当BE⊥AC时,求出此时AE的长.
(3)设AE=x,试探索点E在线段AD上运动过程中,使得△ABE与△BCE相似时,求a、b应满足什么条件,并求出此时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中,AB 两点的坐标分别为 A(1,4),B(5,1),P,Q 分别是 x 轴,y 轴 上两个动点,则四边形 ABPQ 的周长最小值为( )
A.5B.5 ![]() C.
C.![]()
![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣2x+m﹣1=0有两个实数根x1,x2.
(1)求m的取值范围;
(2)当x12+x22=6x1x2时,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
我们可以通过以下方法求代数式![]() 的最小值.
的最小值.
![]() ,
,
∵![]() ≥0,
≥0,
∴当![]() 时,
时, ![]() 有最小值
有最小值![]() .
.
请根据上述方法,解答下列问题:
(1)![]() ,则
,则![]() 的值是______;
的值是______;
(2)求证:无论x取何值,代数式![]() 的值都是正数;
的值都是正数;
(3)若代数式![]() 的最小值为2,求k的值.
的最小值为2,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是边长为4的等边三角形,BC在x轴上,点D为BC的中点,点A在第一象限内,AB与y轴的正半轴交与点E,已知点B(﹣1,0).
(1)点A的坐标: ,点E的坐标: ;
(2)若二次函数y=﹣![]() x2+bx+c过点A、E,求此二次函数的解析式;
x2+bx+c过点A、E,求此二次函数的解析式;
(3)P是线段AC上的一个动点(P与点A、C不重合)连结PB、PD,设L是△PBD的周长,当L取最小值时。
求:①点P的坐标
②判断此时点P是否在(2)中所求的抛物线上,请充分说明你的判断理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
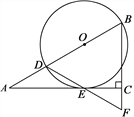
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点D在AB上,以BD为直径的⊙O切AC于点E,连接DE并延长,交BC的延长线于点F.
(1)求证:△BDF是等边三角形;
(2)连接AF、DC,若BC=3,写出求四边形AFCD面积的思路.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com