
【题目】请阅读下列材料:
我们可以通过以下方法求代数式![]() 的最小值.
的最小值.
![]() ,
,
∵![]() ≥0,
≥0,
∴当![]() 时,
时, ![]() 有最小值
有最小值![]() .
.
请根据上述方法,解答下列问题:
(1)![]() ,则
,则![]() 的值是______;
的值是______;
(2)求证:无论x取何值,代数式![]() 的值都是正数;
的值都是正数;
(3)若代数式![]() 的最小值为2,求k的值.
的最小值为2,求k的值.
【答案】-10
【解析】试题分析:(1)根据所作的变形确定出a、b的值即可得;
(2)根据材料中的方法进行变形后,利用平方数的特性即可得证;
(3)根据材料中的方法进行变形后即可进行确定.
试题解析:(1)![]() ,
,
所以a=2,b=-5,所以![]() 的值是-10,
的值是-10,
故答案为:-10;
(2)x2+2![]() x+7=x2+2
x+7=x2+2![]() x+(
x+(![]() )2+7=(x+
)2+7=(x+![]() )2+1,
)2+1,
∵(x+![]() )2≥0,∴x2+2
)2≥0,∴x2+2![]() x+7最小值为1,
x+7最小值为1,
∴无论x取何值,x2+2![]() x+7的值都是正数;
x+7的值都是正数;
(3)2x2+kx+7=(![]() x)2+2×
x)2+2×![]() x×
x×![]() k+(
k+(![]() k)2-(
k)2-(![]() k)2+7=(
k)2+7=(![]() x+
x+![]() )2-
)2-![]() k2+7,
k2+7,
∵(![]() x+
x+![]() )2≥0,
)2≥0,
∴(![]() x+
x+![]() )2-
)2-![]() k2+7的最小值是-
k2+7的最小值是-![]() k2+7,
k2+7,
∴-![]() k2+7=2,
k2+7=2,
∴k=±2![]() .
.


科目:初中数学 来源: 题型:
【题目】几何作图时,我们往往依据以下三个步骤:
①画草图分析思路
②设计画图步骤
③回答结论并验证
请你按照以上所述,完成下面的尺规作图:已知三条线段h,m,c,求作△ABC,使其BC边上的高AH=h,中线AD=m,AB=c.
![]()
(1)请先画草图(画出一个即可),并叙述简要的作图思路(即实现的大致作图步骤);步骤如下:

(2)完成尺规作图(不要求写作法,作出一个满足条件的三角形即可)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,m,n是一元二次方程x2+4x+3=0的两个实数根,且|m|<|n|,抛物线y=x2+bx+c的图象经过点A(m,0),B(0,n),如图所示.
(1)求这个抛物线的解析式;
(2)设(1)中的抛物线与x轴的另一个交点为抛物线的顶点为D,求出点C,D的坐标,并判断△BCD的形状;
(3)点P是直线BC上的一个动点(点P不与点B和点C重合),过点P作x轴的垂线,交抛物线于点M,点Q在直线BC上,距离点P为![]() 个单位长度,设点P的横坐标为t,△PMQ的面积为S,求出S与t之间的函数关系式.
个单位长度,设点P的横坐标为t,△PMQ的面积为S,求出S与t之间的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究
(1)如图①,在△ABC 中,∠B=30°,E 是 AB 边上的点,过点 E 作 EF⊥BC 于 F,则![]() 的值为 .
的值为 .
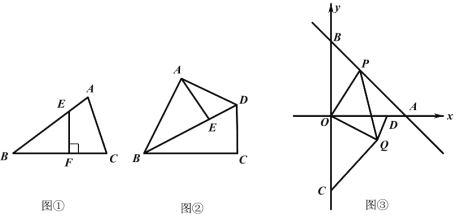
(2)如图②,在四边形 ABCD 中,AB=BC=6,∠ABC=60°,对角线 BD 平分∠ABC,点E 是对角线 BD 上一点,求 AE+ ![]() BE的最小值.
BE的最小值.
问题解决
(3)如图③,在平面直角坐标系中,直线 y -x 4 分别于 x 轴,y 轴交于点 A、B,点 P 为直线 AB 上的动点,以 OP 为边在其下方作等腰 Rt△OPQ 且∠POQ=90°.已知点C(0,-4),点 D(3,0)连接 CQ、DQ,那么DQ ![]() CQ是否存在最小值,若存在求出其最小值及此时点 P 的坐标,若不存在请说明理由.
CQ是否存在最小值,若存在求出其最小值及此时点 P 的坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 于
于![]() ,
,![]() 于
于![]() ,
,![]() 与
与![]() 交于点
交于点![]() .有下列结论:①
.有下列结论:①![]() ≌
≌![]() ;②
;②![]() ≌
≌![]() ;③点
;③点![]() 在
在![]() 的平分线上;④点
的平分线上;④点![]() 在
在![]() 的中垂线上.以上结论正确的有_________________.(填序号)
的中垂线上.以上结论正确的有_________________.(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一对酷爱运动的年轻夫妇给他们12个月大的婴儿拼排3块分别写有“20”,“08”和“北京”的字块,如果婴儿能够排成“2008北京”或者“北京2008”.则他们就给婴儿奖励,假设婴儿能将字块横着正排,那么这个婴儿能得到奖励的概率是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上的任意一点(点
边上的任意一点(点![]() 可以与点
可以与点![]() 重合,但不与点
重合,但不与点![]() 重合).过点
重合).过点![]() 作
作![]() ,垂足为
,垂足为![]() ;点
;点![]() 作
作![]() ,垂足为
,垂足为![]() ;过点
;过点![]() 作
作![]() ,垂足为
,垂足为![]() .设
.设![]() ,
,![]() .
.

(1)用含![]() 的代数式表示
的代数式表示![]() ,并注明
,并注明![]() 的取值范围;
的取值范围;
(2)当![]() 的长等于多少时,点
的长等于多少时,点![]() 和点
和点![]() 重合?
重合?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,⊙O是△ABC的外接圆,![]() =
=![]() ,点D在边BC上,AE∥BC,AE=BD.
,点D在边BC上,AE∥BC,AE=BD.
(1)求证:AD=CE;
(2)如果点G在线段DC上(不与点D重合),且AG=AD,求证:四边形AGCE是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个直径为1m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形ABC,如图所示.
(1)求被剪掉阴影部分的面积:
(2)用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com