
【题目】已知:如图,⊙O是△ABC的外接圆,![]() =
=![]() ,点D在边BC上,AE∥BC,AE=BD.
,点D在边BC上,AE∥BC,AE=BD.
(1)求证:AD=CE;
(2)如果点G在线段DC上(不与点D重合),且AG=AD,求证:四边形AGCE是平行四边形.

【答案】(1)见解析;(2)见解析
【解析】试题分析:(1)根据等弧所对的圆周角相等,得出∠B=∠ACB,再根据全等三角形的判定得△ABD≌△CAE,即可得出AD=CE;
(2)连接AO并延长,交边BC于点H,由等腰三角形的性质和外心的性质得出AH⊥BC,再由垂径定理得BH=CH,得出CG与AE平行且相等.
试题解析:
(1)在⊙O中,
∵![]() =
=![]() ,
,
∴AB=AC,
∴∠B=∠ACB,
∵AE∥BC,
∴∠EAC=∠ACB,
∴∠B=∠EAC,
在△ABD和△CAE中,
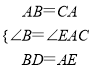 ,
,
∴△ABD≌△CAE(SAS),
∴AD=CE;
(2)易证△ABD≌△ACG得BD=CG,
∵BD=AE,
∴CG=AE,
∵CG∥AE,
∴四边形AGCE是平行四边形.


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
【题目】(14分)如图,已知在矩形ABCD中,AB=a,BC=b,点E是线段AD边上的任意一点(不含端点A、D),连结BE、CE.
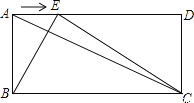
(1)若a=5,AC=13,求b.
(2)若a=5,b=10,当BE⊥AC时,求出此时AE的长.
(3)设AE=x,试探索点E在线段AD上运动过程中,使得△ABE与△BCE相似时,求a、b应满足什么条件,并求出此时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
我们可以通过以下方法求代数式![]() 的最小值.
的最小值.
![]() ,
,
∵![]() ≥0,
≥0,
∴当![]() 时,
时, ![]() 有最小值
有最小值![]() .
.
请根据上述方法,解答下列问题:
(1)![]() ,则
,则![]() 的值是______;
的值是______;
(2)求证:无论x取何值,代数式![]() 的值都是正数;
的值都是正数;
(3)若代数式![]() 的最小值为2,求k的值.
的最小值为2,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是边长为4的等边三角形,BC在x轴上,点D为BC的中点,点A在第一象限内,AB与y轴的正半轴交与点E,已知点B(﹣1,0).
(1)点A的坐标: ,点E的坐标: ;
(2)若二次函数y=﹣![]() x2+bx+c过点A、E,求此二次函数的解析式;
x2+bx+c过点A、E,求此二次函数的解析式;
(3)P是线段AC上的一个动点(P与点A、C不重合)连结PB、PD,设L是△PBD的周长,当L取最小值时。
求:①点P的坐标
②判断此时点P是否在(2)中所求的抛物线上,请充分说明你的判断理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为4,B是⊙O外一点,连接OB,且OB=6,过点B作⊙O的切线BD,切点为D,延长BO交⊙O于点A,过点A作切线BD的垂线,垂足为C.

(1)求证:AD平分∠BAC;
(2)求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学举办“网络安全知识答题竞赛”,初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
平均分(分) | 中位数(分) | 众数(分) | 方差(分2) | |
初中部 | a | 85 | b | s初中2 |
高中部 | 85 | c | 100 | 160 |
(1)根据图示计算出a、b、c的值;
(2)结合两队成绩的平均数和中位数进行分析,哪个队的决赛成绩较好?
(3)计算初中代表队决赛成绩的方差s初中2,并判断哪一个代表队选手成绩较为稳定.

查看答案和解析>>
科目:初中数学 来源: 题型:
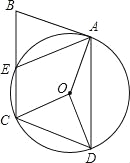
【题目】如图,ABCD的顶点A、C、D都在⊙O上,AB与⊙O相切于点A,BC与⊙O交于点E,设∠OCD=α,∠BAD=β.
(1)求证:AB=AE;
(2)试探究α与β之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
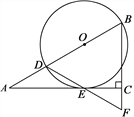
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点D在AB上,以BD为直径的⊙O切AC于点E,连接DE并延长,交BC的延长线于点F.
(1)求证:△BDF是等边三角形;
(2)连接AF、DC,若BC=3,写出求四边形AFCD面积的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
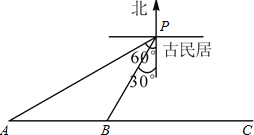
【题目】某市正在进行商业街改造,商业街起点在古民居P的南偏西60°方向上的A处,现已改造至古民居P南偏西30°方向上的B处,A与B相距150m,且B在A的正东方向.为不破坏古民居的风貌,按照有关规定,在古民居周围100m以内不得修建现代化商业街.若工程队继续向正东方向修建200m商业街到C处,则对于从B到C的商业街改造是否违反有关规定?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com