
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点D在AB上,以BD为直径的⊙O切AC于点E,连接DE并延长,交BC的延长线于点F.
(1)求证:△BDF是等边三角形;
(2)连接AF、DC,若BC=3,写出求四边形AFCD面积的思路.
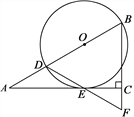
【答案】(1)证明见解析;(2)思路见解析.
【解析】试题分析:(1)连接OE,因AC切⊙O于点E,根据切线的性质可得∠OEA=90° ;再由∠A=30°,∠ACB=90°,根据三角形的内角和定理可得∠AOE=60°,∠B=60°因OD=OE,可得∠ODE=∠OED=60°,所以∠F=∠B=∠ODE,即可判断△BDF是等边三角形 ;(2)如图,作DH⊥AC于点H,求四边形AFCD的面积思路有以下几步:①由∠ACB=90°,∠BAC=30°,BC=3,可求AB,AC的长;②由∠AEO=90°,∠OAE=30°,可知AO=2OE,可求AD,DB,DH的长; ③由(1)可知BF=BD,可求CF的长; ④由AC,DH,CF的长可求四边形AFCD的面积.
试题解析:
(1)证明:连接OE.
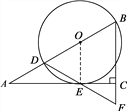
∵AC切⊙O于点E,
∴![]() .
.
∵![]() ,
, ![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴△BDF是等边三角形.
(2)如图,作DH⊥AC于点H.
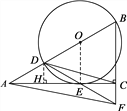
①由∠ACB=90°,∠BAC=30°,BC=3,可求AB,AC的长;
②由∠AEO=90°,∠OAE=30°,可知AO=2OE,可求AD,DB,DH的长;
③由(1)可知BF=BD,可求CF的长;
④由AC,DH,CF的长可求四边形AFCD的面积.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】问题探究
(1)如图①,在△ABC 中,∠B=30°,E 是 AB 边上的点,过点 E 作 EF⊥BC 于 F,则![]() 的值为 .
的值为 .
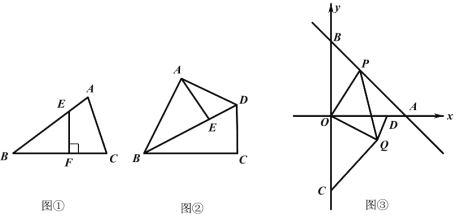
(2)如图②,在四边形 ABCD 中,AB=BC=6,∠ABC=60°,对角线 BD 平分∠ABC,点E 是对角线 BD 上一点,求 AE+ ![]() BE的最小值.
BE的最小值.
问题解决
(3)如图③,在平面直角坐标系中,直线 y -x 4 分别于 x 轴,y 轴交于点 A、B,点 P 为直线 AB 上的动点,以 OP 为边在其下方作等腰 Rt△OPQ 且∠POQ=90°.已知点C(0,-4),点 D(3,0)连接 CQ、DQ,那么DQ ![]() CQ是否存在最小值,若存在求出其最小值及此时点 P 的坐标,若不存在请说明理由.
CQ是否存在最小值,若存在求出其最小值及此时点 P 的坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,⊙O是△ABC的外接圆,![]() =
=![]() ,点D在边BC上,AE∥BC,AE=BD.
,点D在边BC上,AE∥BC,AE=BD.
(1)求证:AD=CE;
(2)如果点G在线段DC上(不与点D重合),且AG=AD,求证:四边形AGCE是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直角△ABC的三个顶点分别是A(﹣3,1),B(0,3),C(0,1)

(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1;
(2)分别连结AB1、BA1后,求四边形AB1A1B的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在八年级开展环保知识问卷调查活动,问卷一共10道题,八年级(三)班的问卷得分情况统计图如下图所示:

(1)扇形统计图中,![]() ______________;
______________;
(2)根据以上统计图中的信息,
①问卷得分的极差是_____________分;②问卷得分的众数是____________分;③问卷得分的中位数是______________分;
(3)请你求出该班同学的平均分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发,在同一条公路上,匀速行驶,相向而行,到两车相遇时停止.甲车行驶一段时间后,因故停车0.5小时,故障解除后,继续以原速向B地行驶,两车之间的路程y(千米)与出发后所用时间x(小时)之间的函数关系如图所示.

(1)求甲、乙两车行驶的速度V甲、V乙.
(2)求m的值.
(3)若甲车没有故障停车,求可以提前多长时间两车相遇.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个直径为1m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形ABC,如图所示.
(1)求被剪掉阴影部分的面积:
(2)用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,OA=OB,AC=CD,已知两点A(4,0),C(0,7),点D在第一象限内,∠DCA=90°,点B在线段OC上,AB的延长线与DC的延长线交于点M,AC与BD交于点N.
(1)点B的坐标为: ;
(2)求点D的坐标;
(3)求证:CM=CN.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=8,AC=5,AD是∠BAC的角平分线,点D在△ABC内部,连接AD、BD、CD,∠ADB=150°,∠DBC=30°,∠ABC+∠ADC=180°,则线段CD的长度为________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com