
【题目】几何作图时,我们往往依据以下三个步骤:
①画草图分析思路
②设计画图步骤
③回答结论并验证
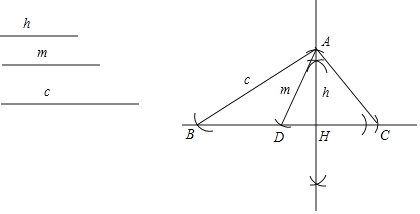
请你按照以上所述,完成下面的尺规作图:已知三条线段h,m,c,求作△ABC,使其BC边上的高AH=h,中线AD=m,AB=c.
![]()
(1)请先画草图(画出一个即可),并叙述简要的作图思路(即实现的大致作图步骤);步骤如下:

(2)完成尺规作图(不要求写作法,作出一个满足条件的三角形即可)

【答案】(1)画草图进行分析先画一条直线,在直线上任意取两点,作线段的垂直平分线,在垂直平分线上截取AD=h,再以点A为圆心,m、c长为半径画弧,交直线于点D、B,以点D为圆心,BD长为半径画弧交直线于点C,即可画出图形,见解析;(2)见解析
【解析】
(1)画草图进行分析先画一条直线,在直线上任意取两点,作线段的垂直平分线,
在垂直平分线上截取AD=h,再以点A为圆心,m、c长为半径画弧,交直线于点D、B,
以点D为圆心,BD长为半径画弧交直线于点C,即可画出图形;
(2)利用尺规作图即可.
解:(1)画草图进行分析先画一条直线,在直线上任意取两点,作线段的垂直平分线,在垂直平分线上截取AD=h,再以点A为圆心,m、c长为半径画弧,交直线于点D、B,以点D为圆心,BD长为半径画弧交直线于点C,即可画出图形;
(2)如图所示:△ABC即为所求作的图形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某公司推出了甲、乙两种新品饮料,它们都由A、B、C三种溶液组成,只是甲种饮料每瓶装有200克A溶液,200克B溶液,100克C溶液;乙种饮料每瓶装有100克A溶液,100克B溶液,300克C溶液,甲、乙两种饮料每瓶成本价均为瓶中A、B、C三种溶液的成本价之和.已知C种溶液每一百克的成本价为1元,乙种饮料每瓶售价为10元,利润率为![]() ,甲种饮料每瓶的利润率为20%,求这两种饮料的销售利润率为24%时,该公司销售甲、乙两种饮料的数量之比是_____.
,甲种饮料每瓶的利润率为20%,求这两种饮料的销售利润率为24%时,该公司销售甲、乙两种饮料的数量之比是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,等边三角形ABC的顶点B与原点O重合,点C在x轴上,点C坐标为(6,0),等边三角形ABC的三边上有三个动点D、E、F(不考虑与A、B、C重合),点D从A向B运动,点E从B向C运动,点F从C向A运动,三点同时运动,到终点结束,且速度均为1cm/s,设运动的时间为ts,解答下列问题:
(1)求证:如图①,不论t如何变化,△DEF始终为等边三角形.
(2)如图②过点E作EQ∥AB,交AC于点Q,设△AEQ的面积为S,求S与t的函数关系式及t为何值时△AEQ的面积最大?求出这个最大值.
(3)在(2)的条件下,当△AEQ的面积最大时,平面内是否存在一点P,使A、D、Q、P构成的四边形是菱形,若存在请直接写出P坐标,若不存在请说明理由?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京世界园艺博览会(简称“世园会”)园区2019年4月29日至2019年10月7日在中国北京市延庆区举行,门票价格如表:小明全家于9月28日集体入园参观游览,通过计算发现:若提前两天线上购买门票所需费用为996元,而入园当天购票所需费用为1080元,则该家庭中可以购买优惠票的有_____人.
票种 | 票价(元/人) | |
指定日 | 普通票 | 160 |
优惠票 | 100 | |
平日 | 普通票 | 120 |
优惠票 | 80 | |
注1:“指定日”为开园日(4月29日)、五一劳动节(5月1日)、端午节、中秋节、十一假期(含闭园日),“平日”为世园会会期除“指定日”外的其他日期;
注2:六十周岁及以上老人、十八周岁以下的学生均可购买优惠票;
注3:提前两天及以上线上购买世园会门票,票价可打九折,但仅限于普通票.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前“微信”、“支付宝”、“共享单车”和“网购”给我们带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行了调查,随机调查了![]() 人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.

(1)根据图中信息求出![]() =___________,
=___________,![]() =_____________;
=_____________;
(2)请你帮助他们将这两个统计图补全;
(3)根据抽样调查的结果,请估算全校2000名学生种,大约有多少人最认可“微信”这一新生事物?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-4x+3.
(1)用配方法求其图象的顶点C的坐标,并描述该函数的函数值随自变量的增减而变化的情况;
(2)求函数图象与x轴的交点A,B的坐标,及△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(14分)如图,已知在矩形ABCD中,AB=a,BC=b,点E是线段AD边上的任意一点(不含端点A、D),连结BE、CE.
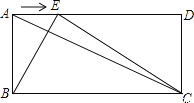
(1)若a=5,AC=13,求b.
(2)若a=5,b=10,当BE⊥AC时,求出此时AE的长.
(3)设AE=x,试探索点E在线段AD上运动过程中,使得△ABE与△BCE相似时,求a、b应满足什么条件,并求出此时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下列材料:
我们可以通过以下方法求代数式![]() 的最小值.
的最小值.
![]() ,
,
∵![]() ≥0,
≥0,
∴当![]() 时,
时, ![]() 有最小值
有最小值![]() .
.
请根据上述方法,解答下列问题:
(1)![]() ,则
,则![]() 的值是______;
的值是______;
(2)求证:无论x取何值,代数式![]() 的值都是正数;
的值都是正数;
(3)若代数式![]() 的最小值为2,求k的值.
的最小值为2,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com