
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��ȱ�������ABC�Ķ���B��ԭ��O�غϣ���C��x���ϣ���C����Ϊ��6��0�����ȱ�������ABC������������������D��E��F����������A��B��C�غϣ�����D��A��B�˶�����E��B��C�˶�����F��C��A�˶�������ͬʱ�˶������յ���������ٶȾ�Ϊ1cm/s�����˶���ʱ��Ϊts������������⣺
��1����֤����ͼ�٣�����t��α仯����DEFʼ��Ϊ�ȱ������Σ�
��2����ͼ�ڹ���E��EQ��AB����AC�ڵ�Q�����AEQ�����ΪS����S��t�ĺ�����ϵʽ��tΪ��ֵʱ��AEQ�����������������ֵ��
��3���ڣ�2���������£�����AEQ��������ʱ��ƽ�����Ƿ����һ��P��ʹA��D��Q��P���ɵ��ı��������Σ���������ֱ��д��P���꣬����������˵�����ɣ�

���𰸡���1��֤������������2����t=3ʱ����AEQ��������Ϊ![]() cm2����3����3��0����6��3
cm2����3����3��0����6��3![]() ����0��3
����0��3![]() ��
��
��������
��1����������ABCΪ�ȱ������Σ��Լ�AD=BE=CF�������ó�������ADF��������CFE��������BEDȫ�ȣ�����ȫ�������ζ�Ӧ����ȵõ�BF=DF=DE�����ɵ�֤����2���ȱ�ʾ��������AEC���������EQ��ABƽ�У��õ�������CEQ��������ABC���ƣ�������������������ȵ������Ʊȵ�ƽ����ʾ��������CEQ�����������ʾ��AEQ��������ö��κ������������������ֵ���������ʱQ�����꼴�ɣ���3������AEQ��������ʱ��D��E��F�����е㣬�������������ۼ� �ɽ�����⣻
��1����ͼ���У�
��C��6��0����
��BC=6
�ڵȱ�������ABC�У�AB=BC=AC=6����A=��B=��C=60�㣬
������֪����0��t��6ʱ��AD=BE=CF=t��
��BD=CE=AF=6��t��
���ADF�ա�CFE�ա�BED��SAS����
��EF=DF=DE��
���DEF�ǵȱ������Σ�
���t��α仯����DEFʼ��Ϊ�ȱ������Σ�

��2����ͼ���У���AH��BC��H����AH=ABsin60��=3![]() ��
��

��S��AEC=![]() ��3
��3![]() ����6��t��=
����6��t��=![]() ��
��
��EQ��AB��
���CEQ�ס�ABC��
��![]() =��
=��![]() ��2=
��2=![]() ����S��CEQ=
����S��CEQ=![]() S��ABC=
S��ABC=![]() ��9
��9![]() =
=![]() ��
��
��S��AEQ=S��AEC��S��CEQ=![]() ��
��![]() =��
=��![]() ��t��3��2+
��t��3��2+![]() ��
��
��a=��![]() ��0��
��0��
�������߿������£������ֵ��
�൱t=3ʱ����AEQ��������Ϊ![]() cm2��
cm2��
��3����ͼ���У��ɣ�2��֪��E��ΪBC���е㣬�߶�EQΪ��ABC����λ�ߣ�

��ADΪ���εı�ʱ���ɵ�P1��3��0����P3��6��3![]() ����
����
��ADΪ�Խ���ʱ��P2��0��3![]() ����
����
�������������������ĵ�P����Ϊ��3��0����6��3![]() ����0��3
����0��3![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ľߵ�ȥ��8�µ�����һ���ľ�1160����Ԥ����9�·ݽ��������������۸�Ϊÿ��10Ԫ�����ۼ�Ϊ12Ԫ/�������ȫ���۳�����ÿ�Ǽ�0.1Ԫ���������ͼ���2����
��1������ľߵ���9�·�������������1100�������ۼ�Ӧ�����ڶ���Ԫ��
��2�����������ã�10�·ݸ��ľ߽��۱�8�µĽ���ÿ������20%���õ��������˽�����������ǿ���������ȣ����10�·ݵ���������9�·��ڣ�1���������µ����������������m%�����ۼ۱�9�·��ڣ�1���������µ�����ۼۼ���![]() m%�����10�·�����ﵽ3388Ԫ����m��ֵ��m��10����
m%�����10�·�����ﵽ3388Ԫ����m��ֵ��m��10����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ 4 �ĵȱ���ABC �У��� D �ӵ�A ��ʼ������ AB ���˶����ٶ�Ϊ 1 ����λ/�룬��F ͬʱ�� C ����������ͬ���ٶ������� BC �����˶�������D �� DE��AC������ DF ������ AC �ڵ� G

(1)�� DF��AB ʱ���� t ��ֵ��
(2)���� D ���߶� AB ���˶�ʱ���Ƿ�ʼ���� DG=GF?����������˵�����ɡ�
(3)������˹��ͬѧͨ���������֣����� D ���߶� AB ��ʱ��EG �ij�ʼ�յ��� AC ��һ�룬���뵱��D �˶���ͼ 2 �����ʱ��EG �ij��Ƿ����仯?���ı䣬˵�����ɣ������䣬��� EG �ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У�AD��BE�Ǹߣ���ABE=45������F��AB���е㣬AD��FE��BE�ֱ��ڵ�G��H����CBE=��BAD�������н��ۣ���FD=FE����AH=2CD����BCAD=![]() AE2����S��BEC=S��ADF��������ȷ���У�������
AE2����S��BEC=S��ADF��������ȷ���У�������

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڸ����ĺ������Ա���ȡx1��x2ʱ����Ӧ�ĺ���ֵ�ֱ��Ϊy1��y2���Ա���ȡ![]() ʱ����Ӧ�ĺ���ֵ��Ϊ
ʱ����Ӧ�ĺ���ֵ��Ϊ![]() ������һ�κ���y��2x+1���Ա���ȡx1��x2ʱ����Ӧ�ĺ���ֵ�ֱ�Ϊy1��2x1+1��y2��2x2+1���Ա���ȡ
������һ�κ���y��2x+1���Ա���ȡx1��x2ʱ����Ӧ�ĺ���ֵ�ֱ�Ϊy1��2x1+1��y2��2x2+1���Ա���ȡ![]() ʱ����Ӧ�ĺ���ֵΪ
ʱ����Ӧ�ĺ���ֵΪ![]() ��2
��2![]() +1�������ڸ����ĺ������Ա���ȡx1��x2��x1��x2��ʱ������
+1�������ڸ����ĺ������Ա���ȡx1��x2��x1��x2��ʱ������![]() ����ƺ���Ϊ���������ڸ����ĺ�������
����ƺ���Ϊ���������ڸ����ĺ�������![]() ����ƺ���Ϊ�������������ڸ����ĺ�������
����ƺ���Ϊ�������������ڸ����ĺ�������![]() ����ƺ���Ϊƽƽ������
����ƺ���Ϊƽƽ������
��1����֤������y��2x��ƽƽ������
��2���жϺ���y��ax2��������������������ƽƽ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����̽������ͼ1���߳�Ϊa�Ĵ�����������һ���߳�Ϊb��С�����Σ���ͼ1�е���Ӱ����ƴ��һ�������Σ���ͼ2��ʾ����ͨ���۲�Ƚ�ͼ2��ͼ1�е���Ӱ������������Եõ��˷���ʽ�� �������ú�a��b�ĵ�ʽ��ʾ��
��Ӧ�ã���Ӧ�������ʽ������и��⣺
��1����֪4m2��12+n2��2m+n��4����2m��n��ֵΪ�� ����
��2�����㣺20192��2020��2018��
����չ�����㣺1002��992+982��972+��+42��32+22��12��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ͼʱ�������������������������裺
�ٻ���ͼ����˼·
����ƻ�ͼ����
�ۻش���۲���֤
���㰴�������������������ij߹���ͼ����֪�����߶�h��m��c��������ABC��ʹ��BC���ϵĸ�AH��h������AD��m��AB��c��
![]()
��1�����Ȼ���ͼ������һ�����ɣ�����������Ҫ����ͼ˼·����ʵ�ֵĴ�����ͼ���裩���������£�

��2����ɳ߹���ͼ����Ҫ��д����������һ�����������������μ��ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y��![]() ��y����kx2��k(k��0)��ͬһ����ϵ��ͼ��������� ��
��y����kx2��k(k��0)��ͬһ����ϵ��ͼ��������� ��
A.  B.
B. 
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������̽��
(1)��ͼ�٣�����ABC �У���B=30����E �� AB ���ϵĵ㣬���� E �� EF��BC �� F����![]() ��ֵΪ .
��ֵΪ .
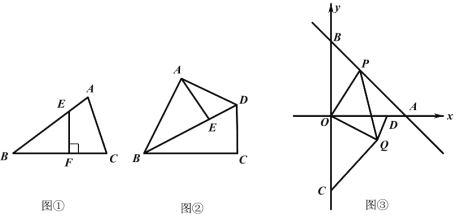
��2����ͼ�ڣ����ı��� ABCD �У�AB=BC=6,��ABC=60�����Խ��� BD ƽ�֡�ABC����E �ǶԽ��� BD ��һ�㣬�� AE+ ![]() BE����Сֵ.
BE����Сֵ.
������
��3����ͼ�ۣ���ƽ��ֱ������ϵ�У�ֱ�� y -x 4 �ֱ��� x �ᣬy �ύ�ڵ� A��B���� P Ϊֱ�� AB �ϵĶ��㣬�� OP Ϊ�������·������� Rt��OPQ �ҡ�POQ=90��.��֪��C��0��-4������ D��3,0������ CQ��DQ,��ôDQ ![]() CQ�Ƿ������Сֵ���������������Сֵ����ʱ�� P �����꣬����������˵������.
CQ�Ƿ������Сֵ���������������Сֵ����ʱ�� P �����꣬����������˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com